Low Pass Filter (LPF) - Filter Pasif
Low Pass Filter adalah rangkaian yang dapat dirancang untuk memodifikasi, membentuk kembali, atau menolak semua frekuensi tinggi dari sinyal listrik dan hanya menerima atau melewatkan sinyal yang diinginkan oleh perancang rangkaian.
Dengan kata lain mereka "menyaring" sinyal yang tidak diinginkan dan filter yang ideal akan memisahkan dan mengeluarkan sinyal input sinusoidal berdasarkan frekuensi mereka.
Dalam aplikasi frekuensi rendah (hingga 100kHz), filter pasif umumnya dibangun menggunakan jaringan RC (Resistor-Capacitor) sederhana, sementara filter frekuensi yang lebih tinggi (di atas 100kHz) biasanya dibuat dari komponen RLC (Resistor-Inductor-Capacitor).
Filter pasif terdiri dari komponen pasif seperti resistor, kapasitor dan induktor dan tidak memiliki elemen penguat (Transistor, Op-amp, dll.) Sehingga tidak memiliki penguatan sinyal, oleh karena itu tingkat outputnya selalu kurang dari input.
Filter dinamai sesuai dengan rentang frekuensi sinyal yang memungkinkannya melewatinya, sambil memblokir atau "melemahkan" sisanya. Desain filter yang paling umum digunakan adalah:
Bergantung pada arah mana kita menghubungkan resistor dan kapasitor sehubungan dengan sinyal output menentukan jenis konstruksi filter yang menghasilkan Low Pass Filter atau High Pass Filter.
Karena fungsi dari filter apa pun adalah untuk memungkinkan sinyal dari pita frekuensi tertentu untuk lewat tanpa diubah saat melemahkan atau atenuasi semua yang tidak diinginkan.
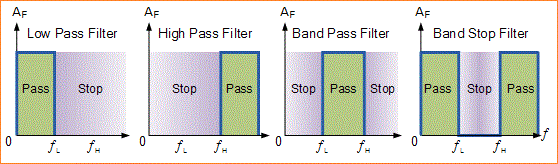
Kita dapat menentukan karakteristik respon amplitudo dari filter ideal dengan menggunakan kurva respons frekuensi ideal dari empat tipe filter dasar seperti yang ditunjukkan.
Filter dapat dibagi menjadi dua jenis: Filter Aktif dan Filter Pasif. Filter Aktif mengandung perangkat penguatan untuk meningkatkan kekuatan sinyal sementara Pasif tidak mengandung perangkat penguatan untuk memperkuat sinyal.
Karena ada dua komponen pasif dalam desain filter pasif, sinyal output memiliki amplitudo yang lebih kecil daripada sinyal input yang sesuai, oleh karena itu filter RC pasif menipiskan sinyal dan memiliki penguatan kurang dari satu, (unity).
Low Pass Filter dapat berupa kombinasi kapasitansi, induktansi atau resistansi yang dimaksudkan untuk menghasilkan atenuasi tinggi di atas frekuensi yang ditentukan dan sedikit atau tidak ada atenuasi di bawah frekuensi tersebut. Frekuensi transisi terjadi disebut frekuensi "cut-off" atau "sudut".
Low Pass Filter paling sederhana terdiri dari resistor dan kapasitor tetapi Low Pass Filter yang lebih canggih memiliki kombinasi induktor seri dan kapasitor paralel. Dalam tutorial ini kita akan melihat jenis yang paling sederhana, dua komponen RC low pass filter pasif.
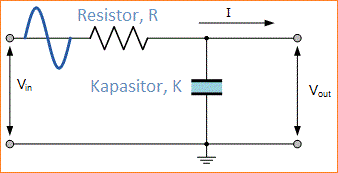
Dalam jenis pengaturan filter ini sinyal input (VIN) diterapkan pada kombinasi seri (baik Resistor dan Kapasitor secara bersamaan) tetapi sinyal output (VOUT) hanya diambil melintasi kapasitor saja.
Jenis filter ini umumnya dikenal sebagai "filter orde-1" atau "filter satu kutub", mengapa orde pertama atau tiang tunggal?, karena hanya memiliki "satu" komponen reaktif, kapasitor, dalam rangkaian.
Seperti disebutkan sebelumnya dalam tutorial Reaktansi Kapasitif, reaktansi kapasitor bervariasi berbanding terbalik dengan frekuensi, sementara nilai resistor tetap konstan seiring perubahan frekuensi.Pada frekuensi rendah reaktansi kapasitif, (XC) dari kapasitor akan sangat besar dibandingkan dengan nilai resistif dari resistor, R.
Ini berarti bahwa potensi tegangan, VC pada kapasitor akan jauh lebih besar dari tegangan drop, VR dikembangkan di resistor. Pada frekuensi tinggi sebaliknya adalah benar dengan VC yang kecil dan VR menjadi besar karena perubahan nilai reaktansi kapasitif.
Sementara rangkaian di atas adalah rangkaian Low Pass Filter RC, ia juga dapat dianggap sebagai rangkaian pembagi potensial variabel dengan frekuensi yang mirip dengan yang kita lihat dalam tutorial Resistor.
Dalam tutorial itu kami menggunakan persamaan berikut untuk menghitung tegangan output untuk dua resistor tunggal yang terhubung secara seri.

Kita juga tahu bahwa reaktansi kapasitif kapasitor dalam rangkaian AC diberikan sebagai:

Perlawanan terhadap aliran arus dalam rangkaian AC disebut Impedansi, simbol Z dan untuk rangkaian seri yang terdiri dari resistor tunggal dalam seri dengan kapasitor tunggal, impedansi rangkaian dihitung sebagai:
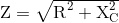
Kemudian dengan mengganti persamaan kami untuk impedansi di atas ke dalam persamaan pembagi potensial resistif memberi kita:
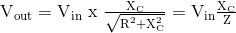
Jadi, dengan menggunakan persamaan pembagi potensial dari dua resistor secara seri dan menggantikan impedansi kita dapat menghitung tegangan output dari Filter RC untuk setiap frekuensi yang diberikan.
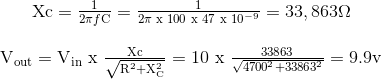

Dengan memplot tegangan output jaringan terhadap nilai frekuensi input yang berbeda, fungsi Kurva Respon Frekuensi atau Bode Plot pada rangkaian Low Pass Filter dapat ditemukan, seperti yang ditunjukkan di bawah ini.
Bode Plot menunjukkan Respon Frekuensi dari filter menjadi hampir rata untuk frekuensi rendah dan semua sinyal input dilewatkan secara langsung ke output, menghasilkan kenaikan hampir 1, disebut kesatuan, hingga mencapai titik Frekuensi Cut-off ( ƒc ). Ini karena reaktansi kapasitor tinggi pada frekuensi rendah dan menghalangi aliran apa pun melalui kapasitor.
Setelah titik frekuensi cut-off ini, respon rangkaian menurun ke nol pada kemiringan -20dB/Decade atau (-6dB/Oktaf) "roll-off". Perhatikan bahwa sudut kemiringan, roll-off -20dB/Decade ini akan selalu sama untuk setiap kombinasi RC.
Setiap sinyal frekuensi tinggi yang diterapkan pada rangkaian Low Pass Filter di atas titik frekuensi cut-off ini akan menjadi sangat dilemahkan, yaitu berkurang dengan cepat.
Hal ini terjadi karena pada frekuensi yang sangat tinggi reaktansi kapasitor menjadi sangat rendah sehingga memberikan efek kondisi hubung singkat pada terminal output yang menghasilkan output nol.
Kemudian dengan hati-hati memilih kombinasi resistor-kapasitor yang benar, kita dapat membuat rangkaian RC yang memungkinkan rentang frekuensi di bawah nilai tertentu untuk melewati rangkaian tanpa terpengaruh sementara frekuensi apa pun yang diterapkan pada rangkaian di atas titik batas ini harus dilemahkan, membuat apa yang biasa disebut Low Pass Filter.
Untuk jenis "Low Pass Filter", semua frekuensi di bawah cut-off ini, titik fc yang tidak berubah dengan sedikit atau tanpa pelemahan/atenuasi dan dikatakan berada di zona Band Pass Filter.
Zona band pass ini juga mewakili Bandwidth dari filter. Frekuensi sinyal apa pun di atas titik cut-off titik ini umumnya dikatakan berada di zona Stop band filter dan mereka akan sangat dilemahkan.
Frekuensi "Cut-off", "Corner/sudut" atau "Breakpoint" ini didefinisikan sebagai titik frekuensi di mana reaktansi dan resistansi kapasitif sama, R = Xc = 4k7Ω.
Ketika ini terjadi sinyal output dilemahkan ke 70.7% dari nilai sinyal input atau -3dB (20 log (Vout/Vin)) dari input. Walaupun R = Xc, output bukan setengah dari sinyal input. Ini karena sama dengan jumlah vektor keduanya dan oleh karena itu 0.707 dari input.
Karena filter berisi kapasitor, Sudut Fasa ( Φ ) sinyal keluaran TERTINGGAL di belakang input dan pada frekuensi cut-off -3dB ( ƒc ) adalah -45° di luar fasa.
Hal ini disebabkan oleh waktu yang diperlukan untuk mengisi plat kapasitor karena perubahan tegangan input, yang mengakibatkan tegangan output (tegangan melintasi kapasitor) "tertinggal" di belakang sinyal input.
Semakin tinggi frekuensi input yang diterapkan pada filter, semakin banyak kapasitor tertinggal dan rangkaian menjadi semakin "keluar dari fasa". Titik frekuensi cut-off dan sudut pergeseran fasa dapat ditemukan dengan menggunakan persamaan berikut:
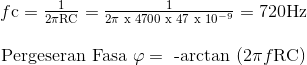
Kemudian untuk contoh sederhana kami dari rangkaian " Low Pass Filter " di atas, frekuensi cut-off ( ƒc ) diberikan sebagai 720Hz dengan tegangan output 70.7% dari nilai tegangan input dan sudut pergeseran fasa -45°.
Namun, kadang-kadang di rangkaian filter ini -20dB/dekade (-6dB/oktaf) sudut kemiringan mungkin tidak cukup untuk menghilangkan sinyal yang tidak diinginkan maka dua tahap penyaringan dapat digunakan seperti yang ditunjukkan.
Rangkaian di atas menggunakan dua filter low-pass pasif orde-1 (pertama) yang terhubung atau "mengalir" bersamaan untuk membentuk jaringan filter orde-2 (dua) atau two-pole.
Oleh karena itu kita dapat melihat bahwa Low Pass Filter orde-1 pertama dapat dikonversi menjadi tipe orde-2 kedua dengan hanya menambahkan jaringan RC tambahan ke dalamnya dan semakin banyak tahapan RC yang kita tambahkan semakin tinggi menjadi orde dari filter.
Jika nomor ( n ) dari tahap RC tersebut mengalir bersama-sama, rangkaian RC filter yang dihasilkan akan dikenal sebagai “orde-n” filter dengan kemiringan roll-off dari “n x -20dB/decade”.
Jadi misalnya, filter orde-2 kedua akan memiliki kemiringan -40dB/decade (-12dB/oktaf), filter orde-4 keempat akan memiliki kemiringan -80dB/decade (-24dB/oktaf) dan seterusnya.
Ini berarti bahwa, ketika orde filter meningkat, kemiringan roll-off menjadi lebih curam dan respon pita henti aktual dari filter mendekati karakteristik pita henti ideal.
Filter Orde-2 kedua yang cukup penting dan banyak digunakan dalam desain filter karena ketika dikombinasikan dengan orde-1 menyaring lebih order-tinggi nilai-n filter dapat dirancang menggunakan mereka.
Sebagai contoh, low-pass filter orde-3 (ketiga) dibentuk dengan menghubungkan secara seri atau mengalir bersama low pass filter orde-1 (pertama) dan orde-2 (kedua).
Tapi ada kelemahannya juga mengalir bersama-sama tahap filter RC. Meskipun tidak ada batasan untuk orde filter yang dapat dibentuk, karena orde meningkat, gain dan keakuratan filter akhir menurun.
Ketika tahapan filter RC identik mengalir bersama-sama, gain output pada frekuensi cut-off yang diperlukan ( ƒc ) dikurangi (dilemahkan) dengan jumlah yang terkait dengan jumlah orde filter yang digunakan saat kemiringan roll-off meningkat. Kita dapat menentukan jumlah atenuasi pada frekuensi cut-off yang dipilih menggunakan rumus berikut.
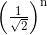
di mana "n" adalah jumlah orde filter.
Jadi untuk Low Pass Filter pasif orde-2 (kedua) gain pada frekuensi sudut ƒc akan sama dengan 0.7071 x 0.7071 = 0.5Vin (-6dB), Low Pass Filter pasif orde-3 (tiga) akan sama dengan 0.353Vin (-9dB), orde-4 (keempat) adalah 0.25Vin (-12dB) dan seterusnya. Frekuensi sudut, ƒc untuk Low Pass Filter pasif orde-2 ditentukan oleh kombinasi resistor/kapasitor (RC) dan diberikan sebagai.
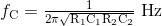
Pada kenyataannya sebagai tahap filter dan oleh karena itu kemiringan roll-offnya meningkat, low pass filter -3dB titik frekuensi sudut dan karenanya frekuensi band pass-nya berubah dari nilai aslinya yang dihitung di atas dengan jumlah yang ditentukan oleh persamaan berikut.
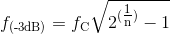
di mana ƒc adalah frekuensi cut-off yang dihitung, n adalah orde filter dan ƒ-3dB adalah frekuensi band pass -3dB baru sebagai akibat dari peningkatan orde filter.
Maka respon frekuensi (blode plot) untuk Low Pass Filter orde-2 kedua dengan asumsi titik cut -3dB yang sama akan terlihat seperti:

Dalam praktiknya, filter pasif mengalir bersama-sama untuk menghasilkan filter orde lebih besar sulit untuk diterapkan secara akurat karena impedansi dinamis dari setiap orde filter mempengaruhi jaringan tetangganya.
Namun, untuk mengurangi efek pembebanan, kita dapat membuat impedansi dari setiap tahap berikut 10x tahap sebelumnya, jadi R2 = 10 x R1 dan C2 = 1/10 C1.
Jaringan filter orde-2 kedua dan di atas umumnya digunakan dalam rangkaian umpan balik Op-amp, menjadikan apa yang umumnya dikenal sebagai Filter Aktif atau sebagai jaringan pemindah fasa di rangkaian Osilator RC.
Rentang frekuensi "di bawah" titik batas ini ƒC umumnya dikenal sebagai Band Pass karena sinyal input diizinkan untuk melewati filter. Rentang frekuensi "di atas" titik cut-off ini umumnya dikenal sebagai Band Stop Filter karena sinyal input diblokir atau berhenti melewatinya.
Low Pass Filter orde-1 pertama sederhana bisa dibuat dengan memakai resistor tunggal tehubung seri dengan kapasitor non-terpolarisasi tunggal (atau komponen reaktif tunggal) pada sinyal input Vin, sedangkan pada sinyal output Vout didapat dari seluruh kapasitor.
Frekuensi cut-off atau titik -3dB, dapat ditemukan menggunakan rumus standar, ƒc = 1 / (2πRC). Sudut fasa dari sinyal output pada ƒc dan -45° untuk Low Pass Filter.
Gain filter atau filter apa pun dalam hal ini, umumnya dinyatakan dalam Desibel dan merupakan fungsi dari nilai output dibagi dengan nilai input yang sesuai dan diberikan sebagai:
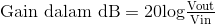
Aplikasi Low Pass Filter pasif biasanya terdapat pada amplifier audio dan sistem speaker fungsinya yaitu untuk mengarahkan sinyal bass frekuensi rendah ke speaker bass yang lebih besar atau digunakan untuk mengurangi kebisingan frekuensi tinggi atau distorsi tipe "desis". Ketika digunakan seperti ini pada aplikasi audio, Low Pass Filter biasanya disebut filter "high-cut", atau "treble cut".
Jika kita membalikkan posisi resistor dan kapasitor di rangkaian sehingga tegangan output sekarang diambil dari resistor, kita akan memiliki rangkaian yang menghasilkan kurva respon frekuensi output yang mirip dengan High Pass Filter, dan ini dibahas dalam tutorial berikutnya.
Kita juga tahu bahwa pergeseran fasa rangkaian tertinggal dari sinyal input karena waktu yang diperlukan untuk mengisi daya dan kemudian melepaskan kapasitor ketika gelombang sinus berubah.
Kombinasi R dan C ini menghasilkan efek pengisian dan pemakaian pada kapasitor yang dikenal sebagai Time Constant (τ) dari rangkaian seperti yang terlihat dalam tutorial Rangkaian RC yang memberikan filter respon pada domain waktu.
Konstanta waktu, tau (τ), terkait dengan frekuensi cut-off ƒc sebagai:
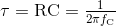
atau dinyatakan dalam hal frekuensi cut-off, ƒc sebagai:

Tegangan output, VOUT tergantung pada konstanta waktu dan frekuensi sinyal input. Dengan sinyal sinusoidal yang berubah dengan lancar dari waktu ke waktu, rangkaian berperilaku sebagai Low Pass Filter orde-1 sederhana seperti yang telah kita lihat di atas.
Tetapi bagaimana jika kita mengubah sinyal input menjadi sinyal tipe "gelombang/persegi" berbentuk "ON/OFF" yang memiliki input langkah hampir vertikal, apa yang akan terjadi pada rangkaian filter kita sekarang. Respon output dari rangkaian akan berubah secara dramatis dan menghasilkan jenis rangkaian lain yang dikenal sebagai Integrator.
Seperti terlihat di bawah, jika konstanta waktu RC panjang dibandingkan dengan periode waktu dari gelombang input, bentuk gelombang output yang dihasilkan akan berbentuk segitiga dan semakin tinggi frekuensi input, semakin rendah amplitudo output dibandingkan dengan input.
Ini kemudian membuat jenis rangkaian ini ideal untuk mengubah satu jenis sinyal elektronik ke jenis lain untuk digunakan dalam rangkaian pembangkit gelombang atau pembentuk gelombang.
Dengan kata lain mereka "menyaring" sinyal yang tidak diinginkan dan filter yang ideal akan memisahkan dan mengeluarkan sinyal input sinusoidal berdasarkan frekuensi mereka.
Dalam aplikasi frekuensi rendah (hingga 100kHz), filter pasif umumnya dibangun menggunakan jaringan RC (Resistor-Capacitor) sederhana, sementara filter frekuensi yang lebih tinggi (di atas 100kHz) biasanya dibuat dari komponen RLC (Resistor-Inductor-Capacitor).
Filter pasif terdiri dari komponen pasif seperti resistor, kapasitor dan induktor dan tidak memiliki elemen penguat (Transistor, Op-amp, dll.) Sehingga tidak memiliki penguatan sinyal, oleh karena itu tingkat outputnya selalu kurang dari input.
Filter dinamai sesuai dengan rentang frekuensi sinyal yang memungkinkannya melewatinya, sambil memblokir atau "melemahkan" sisanya. Desain filter yang paling umum digunakan adalah:
- Low Pass Filter (Pasif) - Low Pass Filter hanya memungkinkan sinyal frekuensi rendah dari 0Hz ke frekuensi cut-off-nya, ƒc point to pass sambil memblokir yang lebih tinggi.
- High Pass Filter (Pasif) - High Pass Filter hanya memungkinkan sinyal frekuensi tinggi dari frekuensi cut-off, titik andc dan lebih tinggi hingga tak terbatas untuk dilewati sambil memblokir yang lebih rendah.
- Band Pass Filter (Pasif) - Band Pass Filter memungkinkan sinyal masuk dalam pengaturan pita frekuensi tertentu antara dua titik untuk dilewati sambil memblokir frekuensi yang lebih rendah dan lebih tinggi di kedua sisi pita frekuensi ini.
- Low Pass Filter (Aktif) -
- High Pass Filter (Aktif) -
- Band Pass Filter (Aktif) -
Bergantung pada arah mana kita menghubungkan resistor dan kapasitor sehubungan dengan sinyal output menentukan jenis konstruksi filter yang menghasilkan Low Pass Filter atau High Pass Filter.
Karena fungsi dari filter apa pun adalah untuk memungkinkan sinyal dari pita frekuensi tertentu untuk lewat tanpa diubah saat melemahkan atau atenuasi semua yang tidak diinginkan.
Kita dapat menentukan karakteristik respon amplitudo dari filter ideal dengan menggunakan kurva respons frekuensi ideal dari empat tipe filter dasar seperti yang ditunjukkan.
Kurva Respon Filter yang Ideal

Filter dapat dibagi menjadi dua jenis: Filter Aktif dan Filter Pasif. Filter Aktif mengandung perangkat penguatan untuk meningkatkan kekuatan sinyal sementara Pasif tidak mengandung perangkat penguatan untuk memperkuat sinyal.
Karena ada dua komponen pasif dalam desain filter pasif, sinyal output memiliki amplitudo yang lebih kecil daripada sinyal input yang sesuai, oleh karena itu filter RC pasif menipiskan sinyal dan memiliki penguatan kurang dari satu, (unity).
Low Pass Filter dapat berupa kombinasi kapasitansi, induktansi atau resistansi yang dimaksudkan untuk menghasilkan atenuasi tinggi di atas frekuensi yang ditentukan dan sedikit atau tidak ada atenuasi di bawah frekuensi tersebut. Frekuensi transisi terjadi disebut frekuensi "cut-off" atau "sudut".
Low Pass Filter paling sederhana terdiri dari resistor dan kapasitor tetapi Low Pass Filter yang lebih canggih memiliki kombinasi induktor seri dan kapasitor paralel. Dalam tutorial ini kita akan melihat jenis yang paling sederhana, dua komponen RC low pass filter pasif.
Low Pass Filter (LPF) - Pasif
Low Pass Filter pasif RC sederhana, dapat dengan mudah dibuat dengan menghubungkan bersama-sama dalam rangkaian Resistor tunggal dengan Kapasitor tunggal seperti yang ditunjukkan di bawah ini.Dalam jenis pengaturan filter ini sinyal input (VIN) diterapkan pada kombinasi seri (baik Resistor dan Kapasitor secara bersamaan) tetapi sinyal output (VOUT) hanya diambil melintasi kapasitor saja.
Jenis filter ini umumnya dikenal sebagai "filter orde-1" atau "filter satu kutub", mengapa orde pertama atau tiang tunggal?, karena hanya memiliki "satu" komponen reaktif, kapasitor, dalam rangkaian.
Rangkaian Low Pass Filter (LPF)

Seperti disebutkan sebelumnya dalam tutorial Reaktansi Kapasitif, reaktansi kapasitor bervariasi berbanding terbalik dengan frekuensi, sementara nilai resistor tetap konstan seiring perubahan frekuensi.Pada frekuensi rendah reaktansi kapasitif, (XC) dari kapasitor akan sangat besar dibandingkan dengan nilai resistif dari resistor, R.
Ini berarti bahwa potensi tegangan, VC pada kapasitor akan jauh lebih besar dari tegangan drop, VR dikembangkan di resistor. Pada frekuensi tinggi sebaliknya adalah benar dengan VC yang kecil dan VR menjadi besar karena perubahan nilai reaktansi kapasitif.
Sementara rangkaian di atas adalah rangkaian Low Pass Filter RC, ia juga dapat dianggap sebagai rangkaian pembagi potensial variabel dengan frekuensi yang mirip dengan yang kita lihat dalam tutorial Resistor.
Dalam tutorial itu kami menggunakan persamaan berikut untuk menghitung tegangan output untuk dua resistor tunggal yang terhubung secara seri.

Kita juga tahu bahwa reaktansi kapasitif kapasitor dalam rangkaian AC diberikan sebagai:

Perlawanan terhadap aliran arus dalam rangkaian AC disebut Impedansi, simbol Z dan untuk rangkaian seri yang terdiri dari resistor tunggal dalam seri dengan kapasitor tunggal, impedansi rangkaian dihitung sebagai:
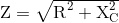
Kemudian dengan mengganti persamaan kami untuk impedansi di atas ke dalam persamaan pembagi potensial resistif memberi kita:
Persamaan Potensi Pembagi Filter RC
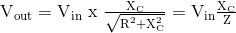
Jadi, dengan menggunakan persamaan pembagi potensial dari dua resistor secara seri dan menggantikan impedansi kita dapat menghitung tegangan output dari Filter RC untuk setiap frekuensi yang diberikan.
Contoh: Low Pass Filter (LPF) - Filter Pasif No.1
Sebuah rangkaian Low Pass Filter yang terdiri dari resistor dari 4k7Ω secara seri dengan sebuah kapasitor dari 47nF dihubungkan dengan sebuah 10V supply sinusoidal. Hitung tegangan output ( VOUT ) pada frekuensi 100Hz dan lagi pada frekuensi 10.000Hz atau 10kHz.Output Tegangan pada Frekuensi 100Hz.
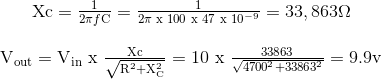
Output Tegangan pada Frekuensi 10.000Hz (10kHz).

Respon Frekuensi
Kita dapat melihat dari hasil di atas, bahwa ketika frekuensi yang diterapkan pada jaringan RC meningkat dari 100Hz ke 10kHz, tegangan turun melintasi kapasitor dan oleh karena itu tegangan output ( VOUT) dari rangkaian menurun dari 9.9v ke 0.718v.Dengan memplot tegangan output jaringan terhadap nilai frekuensi input yang berbeda, fungsi Kurva Respon Frekuensi atau Bode Plot pada rangkaian Low Pass Filter dapat ditemukan, seperti yang ditunjukkan di bawah ini.
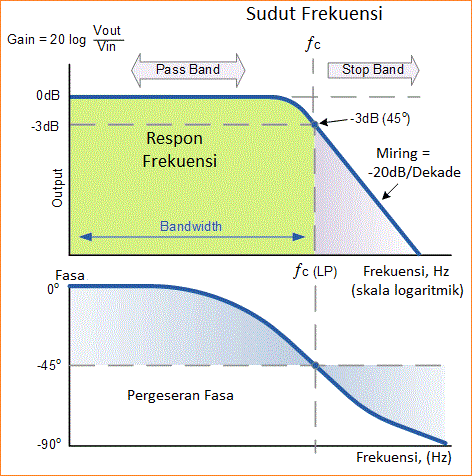
Respon Frekuensi dari Low Pass Filter Orde-1 (pertama)

Bode Plot menunjukkan Respon Frekuensi dari filter menjadi hampir rata untuk frekuensi rendah dan semua sinyal input dilewatkan secara langsung ke output, menghasilkan kenaikan hampir 1, disebut kesatuan, hingga mencapai titik Frekuensi Cut-off ( ƒc ). Ini karena reaktansi kapasitor tinggi pada frekuensi rendah dan menghalangi aliran apa pun melalui kapasitor.
Setelah titik frekuensi cut-off ini, respon rangkaian menurun ke nol pada kemiringan -20dB/Decade atau (-6dB/Oktaf) "roll-off". Perhatikan bahwa sudut kemiringan, roll-off -20dB/Decade ini akan selalu sama untuk setiap kombinasi RC.
Setiap sinyal frekuensi tinggi yang diterapkan pada rangkaian Low Pass Filter di atas titik frekuensi cut-off ini akan menjadi sangat dilemahkan, yaitu berkurang dengan cepat.
Hal ini terjadi karena pada frekuensi yang sangat tinggi reaktansi kapasitor menjadi sangat rendah sehingga memberikan efek kondisi hubung singkat pada terminal output yang menghasilkan output nol.
Kemudian dengan hati-hati memilih kombinasi resistor-kapasitor yang benar, kita dapat membuat rangkaian RC yang memungkinkan rentang frekuensi di bawah nilai tertentu untuk melewati rangkaian tanpa terpengaruh sementara frekuensi apa pun yang diterapkan pada rangkaian di atas titik batas ini harus dilemahkan, membuat apa yang biasa disebut Low Pass Filter.
Untuk jenis "Low Pass Filter", semua frekuensi di bawah cut-off ini, titik fc yang tidak berubah dengan sedikit atau tanpa pelemahan/atenuasi dan dikatakan berada di zona Band Pass Filter.
Zona band pass ini juga mewakili Bandwidth dari filter. Frekuensi sinyal apa pun di atas titik cut-off titik ini umumnya dikatakan berada di zona Stop band filter dan mereka akan sangat dilemahkan.
Frekuensi "Cut-off", "Corner/sudut" atau "Breakpoint" ini didefinisikan sebagai titik frekuensi di mana reaktansi dan resistansi kapasitif sama, R = Xc = 4k7Ω.
Ketika ini terjadi sinyal output dilemahkan ke 70.7% dari nilai sinyal input atau -3dB (20 log (Vout/Vin)) dari input. Walaupun R = Xc, output bukan setengah dari sinyal input. Ini karena sama dengan jumlah vektor keduanya dan oleh karena itu 0.707 dari input.
Karena filter berisi kapasitor, Sudut Fasa ( Φ ) sinyal keluaran TERTINGGAL di belakang input dan pada frekuensi cut-off -3dB ( ƒc ) adalah -45° di luar fasa.
Hal ini disebabkan oleh waktu yang diperlukan untuk mengisi plat kapasitor karena perubahan tegangan input, yang mengakibatkan tegangan output (tegangan melintasi kapasitor) "tertinggal" di belakang sinyal input.
Semakin tinggi frekuensi input yang diterapkan pada filter, semakin banyak kapasitor tertinggal dan rangkaian menjadi semakin "keluar dari fasa". Titik frekuensi cut-off dan sudut pergeseran fasa dapat ditemukan dengan menggunakan persamaan berikut:
Frekuensi Cut-off dan Pergeseran Fasa
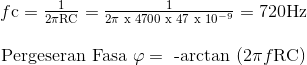
Kemudian untuk contoh sederhana kami dari rangkaian " Low Pass Filter " di atas, frekuensi cut-off ( ƒc ) diberikan sebagai 720Hz dengan tegangan output 70.7% dari nilai tegangan input dan sudut pergeseran fasa -45°.
Low Pass Filter Orde-2 (kedua)
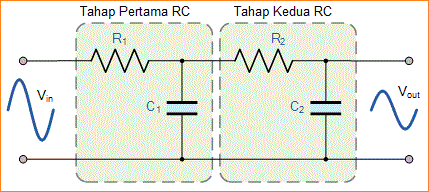
Sejauh ini kita telah melihat bahwa low pass filter - RC orde-1 (pertama) sederhana dapat dibuat dengan menghubungkan satu resistor secara seri dengan kapasitor tunggal. Pengaturan single-pole ini memberi kita kemiringan roll-off atenuasi 20dB / dekade frekuensi di atas titik cut-off di ƒ-3dB.Namun, kadang-kadang di rangkaian filter ini -20dB/dekade (-6dB/oktaf) sudut kemiringan mungkin tidak cukup untuk menghilangkan sinyal yang tidak diinginkan maka dua tahap penyaringan dapat digunakan seperti yang ditunjukkan.
Rangkaian Low Pass Filter Orde-2 (kedua)

Rangkaian di atas menggunakan dua filter low-pass pasif orde-1 (pertama) yang terhubung atau "mengalir" bersamaan untuk membentuk jaringan filter orde-2 (dua) atau two-pole.
Oleh karena itu kita dapat melihat bahwa Low Pass Filter orde-1 pertama dapat dikonversi menjadi tipe orde-2 kedua dengan hanya menambahkan jaringan RC tambahan ke dalamnya dan semakin banyak tahapan RC yang kita tambahkan semakin tinggi menjadi orde dari filter.
Jika nomor ( n ) dari tahap RC tersebut mengalir bersama-sama, rangkaian RC filter yang dihasilkan akan dikenal sebagai “orde-n” filter dengan kemiringan roll-off dari “n x -20dB/decade”.
Jadi misalnya, filter orde-2 kedua akan memiliki kemiringan -40dB/decade (-12dB/oktaf), filter orde-4 keempat akan memiliki kemiringan -80dB/decade (-24dB/oktaf) dan seterusnya.
Ini berarti bahwa, ketika orde filter meningkat, kemiringan roll-off menjadi lebih curam dan respon pita henti aktual dari filter mendekati karakteristik pita henti ideal.
Filter Orde-2 kedua yang cukup penting dan banyak digunakan dalam desain filter karena ketika dikombinasikan dengan orde-1 menyaring lebih order-tinggi nilai-n filter dapat dirancang menggunakan mereka.
Sebagai contoh, low-pass filter orde-3 (ketiga) dibentuk dengan menghubungkan secara seri atau mengalir bersama low pass filter orde-1 (pertama) dan orde-2 (kedua).
Tapi ada kelemahannya juga mengalir bersama-sama tahap filter RC. Meskipun tidak ada batasan untuk orde filter yang dapat dibentuk, karena orde meningkat, gain dan keakuratan filter akhir menurun.
Ketika tahapan filter RC identik mengalir bersama-sama, gain output pada frekuensi cut-off yang diperlukan ( ƒc ) dikurangi (dilemahkan) dengan jumlah yang terkait dengan jumlah orde filter yang digunakan saat kemiringan roll-off meningkat. Kita dapat menentukan jumlah atenuasi pada frekuensi cut-off yang dipilih menggunakan rumus berikut.
Gain Low Pass Filter Pasif di ƒc
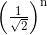
di mana "n" adalah jumlah orde filter.
Jadi untuk Low Pass Filter pasif orde-2 (kedua) gain pada frekuensi sudut ƒc akan sama dengan 0.7071 x 0.7071 = 0.5Vin (-6dB), Low Pass Filter pasif orde-3 (tiga) akan sama dengan 0.353Vin (-9dB), orde-4 (keempat) adalah 0.25Vin (-12dB) dan seterusnya. Frekuensi sudut, ƒc untuk Low Pass Filter pasif orde-2 ditentukan oleh kombinasi resistor/kapasitor (RC) dan diberikan sebagai.
Frekuensi Corner (sudut) Filter Orde-2 Kedua
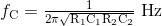
Pada kenyataannya sebagai tahap filter dan oleh karena itu kemiringan roll-offnya meningkat, low pass filter -3dB titik frekuensi sudut dan karenanya frekuensi band pass-nya berubah dari nilai aslinya yang dihitung di atas dengan jumlah yang ditentukan oleh persamaan berikut.
Low Pass Filter Orde-2 Kedua Frekuensi -3dB
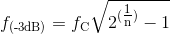
di mana ƒc adalah frekuensi cut-off yang dihitung, n adalah orde filter dan ƒ-3dB adalah frekuensi band pass -3dB baru sebagai akibat dari peningkatan orde filter.
Maka respon frekuensi (blode plot) untuk Low Pass Filter orde-2 kedua dengan asumsi titik cut -3dB yang sama akan terlihat seperti:
Respon Frekuensi dari Low Pass Filter Orde-2 Kedua

Dalam praktiknya, filter pasif mengalir bersama-sama untuk menghasilkan filter orde lebih besar sulit untuk diterapkan secara akurat karena impedansi dinamis dari setiap orde filter mempengaruhi jaringan tetangganya.
Namun, untuk mengurangi efek pembebanan, kita dapat membuat impedansi dari setiap tahap berikut 10x tahap sebelumnya, jadi R2 = 10 x R1 dan C2 = 1/10 C1.
Jaringan filter orde-2 kedua dan di atas umumnya digunakan dalam rangkaian umpan balik Op-amp, menjadikan apa yang umumnya dikenal sebagai Filter Aktif atau sebagai jaringan pemindah fasa di rangkaian Osilator RC.
Ringkasan Low Pass Filter (LPF) - Filter Pasif
Jadi untuk meringkas, Low Pass Filter memiliki tegangan output konstan dari DC (0Hz), hingga frekuensi tertentu Cut-off, ( ƒC ). Titik frekuensi cut-off ini adalah 0.707 atau -3dB (dB = –20log*VOUT/IN) dari kenaikan tegangan yang diizinkan untuk dilewati.Rentang frekuensi "di bawah" titik batas ini ƒC umumnya dikenal sebagai Band Pass karena sinyal input diizinkan untuk melewati filter. Rentang frekuensi "di atas" titik cut-off ini umumnya dikenal sebagai Band Stop Filter karena sinyal input diblokir atau berhenti melewatinya.
Low Pass Filter orde-1 pertama sederhana bisa dibuat dengan memakai resistor tunggal tehubung seri dengan kapasitor non-terpolarisasi tunggal (atau komponen reaktif tunggal) pada sinyal input Vin, sedangkan pada sinyal output Vout didapat dari seluruh kapasitor.
Frekuensi cut-off atau titik -3dB, dapat ditemukan menggunakan rumus standar, ƒc = 1 / (2πRC). Sudut fasa dari sinyal output pada ƒc dan -45° untuk Low Pass Filter.
Gain filter atau filter apa pun dalam hal ini, umumnya dinyatakan dalam Desibel dan merupakan fungsi dari nilai output dibagi dengan nilai input yang sesuai dan diberikan sebagai:
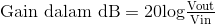
Aplikasi Low Pass Filter pasif biasanya terdapat pada amplifier audio dan sistem speaker fungsinya yaitu untuk mengarahkan sinyal bass frekuensi rendah ke speaker bass yang lebih besar atau digunakan untuk mengurangi kebisingan frekuensi tinggi atau distorsi tipe "desis". Ketika digunakan seperti ini pada aplikasi audio, Low Pass Filter biasanya disebut filter "high-cut", atau "treble cut".
Jika kita membalikkan posisi resistor dan kapasitor di rangkaian sehingga tegangan output sekarang diambil dari resistor, kita akan memiliki rangkaian yang menghasilkan kurva respon frekuensi output yang mirip dengan High Pass Filter, dan ini dibahas dalam tutorial berikutnya.
Waktu Konstan
Sampai sekarang kami telah tertarik pada respon frekuensi Low Pass Filter ketika mengalami gelombang sinusoidal. Kita juga telah melihat bahwa frekuensi cut-off filter (ƒc) adalah hasil dari resistansi (R) dan kapasitansi (C) dalam rangkaian sehubungan dengan beberapa titik frekuensi tertentu dan dengan mengubah salah satu dari dua komponen yang diubah. titik frekuensi cut-off ini dengan meningkatkan atau menguranginya.Kita juga tahu bahwa pergeseran fasa rangkaian tertinggal dari sinyal input karena waktu yang diperlukan untuk mengisi daya dan kemudian melepaskan kapasitor ketika gelombang sinus berubah.
Kombinasi R dan C ini menghasilkan efek pengisian dan pemakaian pada kapasitor yang dikenal sebagai Time Constant (τ) dari rangkaian seperti yang terlihat dalam tutorial Rangkaian RC yang memberikan filter respon pada domain waktu.
Konstanta waktu, tau (τ), terkait dengan frekuensi cut-off ƒc sebagai:
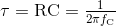
atau dinyatakan dalam hal frekuensi cut-off, ƒc sebagai:

Tegangan output, VOUT tergantung pada konstanta waktu dan frekuensi sinyal input. Dengan sinyal sinusoidal yang berubah dengan lancar dari waktu ke waktu, rangkaian berperilaku sebagai Low Pass Filter orde-1 sederhana seperti yang telah kita lihat di atas.
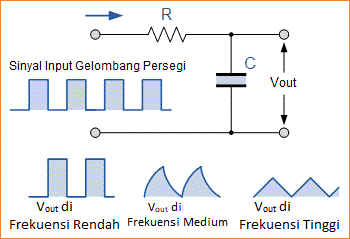
Tetapi bagaimana jika kita mengubah sinyal input menjadi sinyal tipe "gelombang/persegi" berbentuk "ON/OFF" yang memiliki input langkah hampir vertikal, apa yang akan terjadi pada rangkaian filter kita sekarang. Respon output dari rangkaian akan berubah secara dramatis dan menghasilkan jenis rangkaian lain yang dikenal sebagai Integrator.
Integrator RC
Integrator pada dasarnya adalah sebuah rangkaian low pass filter yang beroperasi dalam domain waktu yang mengubah gelombang “langkah” sinyal input respon persegi menjadi output gelombang berbentuk segitiga sebagai muatan kapasitor dan kotoran. Bentuk gelombang segitiga terdiri atas jalur landai yang bergantian tetapi sama, positif dan negatif.Seperti terlihat di bawah, jika konstanta waktu RC panjang dibandingkan dengan periode waktu dari gelombang input, bentuk gelombang output yang dihasilkan akan berbentuk segitiga dan semakin tinggi frekuensi input, semakin rendah amplitudo output dibandingkan dengan input.
Rangkaian Integrator RC

Ini kemudian membuat jenis rangkaian ini ideal untuk mengubah satu jenis sinyal elektronik ke jenis lain untuk digunakan dalam rangkaian pembangkit gelombang atau pembentuk gelombang.