Gelombang Sinusoidal
Ketika arus listrik mengalir melalui kawat atau konduktor, medan magnet melingkar dibuat di sekitar kawat dan yang kekuatannya terkait dengan nilai arus. Jika konduktor kawat tunggal ini dipindahkan atau diputar dalam medan magnet stasioner, "GGL", (Gaya Gerak Listrik) diinduksi dalam konduktor karena pergerakan konduktor melalui fluks magnet.
Dari sini kita dapat melihat bahwa ada hubungan antara Listrik dan Magnet, ketika Michael Faraday menemukan efek "Induksi Elektromagnetik". Dan prinsip dasar inilah yang digunakan mesin dan generator listrik untuk menghasilkan Gelombang Sinusoidal untuk pasokan listrik utama kita.
Dalam tutorial Induksi Elektromagnetik, kami mengatakan bahwa ketika konduktor kawat tunggal bergerak melalui medan magnet permanen sehingga memotong garis fluksnya, GGL diinduksi di dalamnya.

Namun, jika konduktor bergerak secara paralel dengan medan magnet dalam kasus titik A dan B, tidak ada garis fluks yang terpotong dan tidak ada GGL (Gaya Gerak Listrik) yang diinduksi ke dalam konduktor.
Tetapi jika konduktor bergerak pada sudut kanan ke medan magnet seperti pada kasus titik C dan D , jumlah maksimum fluks magnetik dipotong menghasilkan jumlah maksimum GGL terinduksi.
Juga, ketika konduktor memotong medan magnet pada sudut yang berbeda antara titik A dan C, 0 dan 90° jumlah GGL terinduksi akan terletak di suatu tempat antara nol dan nilai maksimum ini.
Kemudian jumlah ggl yang diinduksi dalam konduktor tergantung pada sudut antara konduktor dan fluks magnet serta kekuatan medan magnet.
Generator AC menggunakan prinsip induksi elektromagnetik Faraday untuk mengubah energi mekanik seperti rotasi, menjadi energi listrik, gelombang sinusoidal.
Generator sederhana terdiri dari sepasang magnet permanen yang menghasilkan medan magnet tetap antara kutub utara dan selatan.
Di dalam medan magnet ini ada satu lingkaran persegi panjang kawat yang dapat diputar di sekitar sumbu tetap yang memungkinkannya memotong fluks magnet pada berbagai sudut seperti ditunjukkan di bawah ini.

Ketika kumparan berputar berlawanan arah jarum jam di sekitar sumbu pusat yang tegak lurus terhadap medan magnet, loop kawat memotong garis-garis gaya magnet yang diatur antara kutub utara dan selatan pada sudut yang berbeda saat loop berputar. Jumlah GGL terinduksi dalam loop pada setiap saat waktu sebanding dengan sudut rotasi loop kawat.
Saat loop kawat ini berputar, elektron-elektron dalam kawat mengalir dalam satu arah di sekitar loop. Sekarang ketika loop kawat telah diputar melewati 180° titik dan bergerak di garis gaya magnetik dalam arah yang berlawanan, elektron dalam kawat perubahan lingkaran dan mengalir dalam arah yang berlawanan. Kemudian arah gerakan elektron menentukan polaritas tegangan yang diinduksi.
Jadi kita dapat melihat bahwa ketika loop atau kumparan secara fisik memutar satu putaran penuh, atau 360°, satu gelombang sinusoidal penuh diproduksi dengan satu siklus bentuk gelombang yang diproduksi untuk setiap putaran kumparan.
Ketika kumparan berputar di dalam medan magnet, sambungan listrik dibuat ke kumparan dengan menggunakan sikat karbon dan cincin selip yang digunakan untuk mentransfer arus listrik yang diinduksi dalam kumparan.
Jumlah GGL yang diinduksi ke dalam kumparan memotong garis gaya magnet ditentukan oleh tiga faktor berikut.
Karena satu siklus ggl (gaya gerak listrik) yang diinduksi diproduksi setiap putaran penuh kumparan melalui medan magnet yang terdiri dari kutub utara dan selatan seperti yang ditunjukkan di atas.
Jika kumparan berputar pada kecepatan konstan, jumlah siklus yang konstan akan dihasilkan per detik memberikan konstanta frekuensi.
Jadi dengan meningkatkan kecepatan putaran kumparan, frekuensi juga akan meningkat. Oleh karena itu, frekuensi sebanding dengan kecepatan rotasi, ( ƒ ∝ Ν ) di mana Ν = r.p.m
Selain itu, generator kumparan tunggal kami yang sederhana di atas hanya memiliki dua kutub, satu kutub utara dan satu kutub selatan, yang hanya memberikan satu pasang kutub.
Jika kita menambahkan lebih banyak kutub magnet pada generator di atas sehingga sekarang memiliki empat kutub total, dua utara dan dua selatan, maka untuk setiap putaran kumparan, dua siklus akan diproduksi untuk kecepatan rotasi yang sama.
Oleh karena itu, frekuensi sebanding dengan jumlah pasangan kutub magnet, ( ƒ ∝ P ) dari generator di mana P = jumlah "pasangan kutub".
Kemudian dari dua fakta ini kita dapat mengatakan bahwa output frekuensi dari generator AC adalah:
frekuensi generator
f α N, dan f α P
∴ f = N x P di siklus/min
sebagai Frekuensi diukur di Hertz

Di mana: Ν adalah kecepatan rotasi dalam r.p.m. P adalah jumlah "pasang kutub" dan 60 mengubahnya menjadi detik.
Karena bentuk gelombang AC secara konstan mengubah nilainya atau amplitudo, bentuk gelombang pada saat kapan saja akan memiliki nilai yang berbeda dari gelombang berikutnya.
Misalnya, nilai pada 1ms akan berbeda dengan nilai pada 1.2 ms dan seterusnya. Nilai-nilai ini umumnya dikenal sebagai Nilai Instan, atau Vi.
Kemudian nilai sesaat dari bentuk gelombang dan juga arahnya akan bervariasi sesuai dengan posisi kumparan dalam medan magnet seperti yang ditunjukkan di bawah ini.
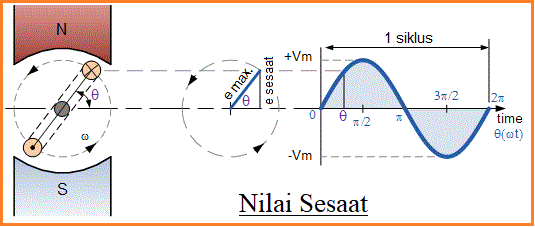
Nilai sesaat dari bentuk gelombang sinusoidal diberikan sebagai "Nilai sesaat = Nilai maksimum x sin θ" dan ini digeneralisasi oleh rumus.
Vi = Vmax x sinθ
Dimana, Vmax adalah tegangan maksimum diinduksi dalam kumparan dan θ = ωt, adalah sudut rotasi dari kumparan terhadap waktu. Jika kita mengetahui nilai maksimum atau puncak gelombang, dengan menggunakan rumus di atas nilai sesaat di berbagai titik di sepanjang gelombang dapat dihitung.
Dengan memplot nilai-nilai ini ke kertas grafik, bentuk gelombang sinusoidal dapat dibangun. Untuk mempermudah, kami akan memplot nilai sesaat untuk bentuk gelombang sinusoidal pada setiap 45° rotasi memberi kita 8 poin untuk plot.
Sekali lagi, untuk membuatnya tetap sederhana, kita akan mengasumsikan tegangan maksimum, nilai Vmax 100V.
Merencanakan nilai sesaat pada interval yang lebih pendek, misalnya pada setiap 30° (12 titik) atau 10° (36 titik) misalnya akan menghasilkan konstruksi gelombang sinusoidal yang lebih akurat.

Titik-titik pada gelombang sinusoidal diperoleh dengan memproyeksikan seberang berbagai posisi rotasi antara 0° dan 360° ke ordinat dari bentuk gelombang yang sesuai dengan sudut, θ dan ketika kawat loop atau kumparan berputar satu putaran penuh, atau 360°, satu bentuk gelombang penuh diproduksi.
Dari plot bentuk gelombang sinusoidal kita dapat melihat bahwa ketika θ sama dengan 0°, 180° atau 360°, yang dihasilkan GGL adalah nol sebagai kumparan memotong jumlah minimum garis fluks.
Tetapi ketika θ sama dengan 90° dan 270° GGL yang dihasilkan berada pada nilai maksimumnya ketika jumlah fluks maksimum dipotong.
Oleh karena itu bentuk gelombang sinusoidal memiliki puncak positif pada 90° dan puncak negatif pada 270°. Posisi B, D, F dan H menghasilkan nilai GGL yang sesuai dengan rumus: e = Vmax.sinθ .
Kemudian bentuk gelombang yang dihasilkan oleh generator loop tunggal sederhana kami biasanya disebut sebagai Gelombang Sinus karena dikatakan berbentuk sinusoidal.
Jenis gelombang ini disebut gelombang sinus karena didasarkan pada fungsi sinus trigonometri yang digunakan dalam matematika, ( x (t) = Amax.sinθ ).
Ketika berhadapan dengan gelombang sinus dalam domain waktu dan khususnya gelombang sinus terkait saat ini, unit pengukuran yang digunakan sepanjang sumbu horizontal dari bentuk gelombang dapat berupa waktu, derajat atau radian.
Dalam teknik elektro, lebih umum menggunakan Radian sebagai pengukuran sudut sudut sepanjang sumbu horizontal daripada derajat.
Misalnya, ω = 100 rad/s, atau 500 rad/s.
Karena keliling lingkaran sama dengan 2π radius x , harus ada 2π radian sekitar 360° lingkaran.
Dengan kata lain, radian adalah satuan pengukuran sudut dan panjang satu radian (r) akan sesuai dengan 6,284 (2*π) kali di sekitar seluruh lingkaran.
Jadi satu radian sama dengan 360°/2π = 57,3°. Dalam teknik elektro, penggunaan radian sangat umum sehingga penting untuk mengingat rumus berikut.

2π rad = 360°
Menggunakan radian sebagai unit pengukuran untuk gelombang sinusoidal akan memberikan 2π radian untuk satu siklus penuh 360°.
Kemudian setengah bentuk gelombang sinusoidal harus sama dengan 1π radian atau hanya π (pi). Maka mengetahui bahwa pi, ( π ) sama dengan 3.142, hubungan antara derajat dan radian untuk bentuk gelombang sinusoidal diberikan sebagai:

Menerapkan dua persamaan ini ke berbagai titik di sepanjang bentuk gelombang memberi kita.

Konversi antara derajat dan radian untuk persamaan yang lebih umum digunakan dalam analisis sinusoidal diberikan dalam tabel berikut.

Kecepatan di mana generator berputar di sekitar poros pusatnya menentukan frekuensi gelombang sinusoidal. Karena frekuensi bentuk gelombang diberikan sebagai ƒ Hz atau siklus per detik, bentuk gelombang juga memiliki frekuensi sudut, ω, (huruf Yunani omega), dalam radian per detik.
Kemudian kecepatan sudut dari bentuk gelombang sinusoidal diberikan sebagai.
Kita tahu dari atas bahwa ekspresi umum yang diberikan untuk bentuk gelombang sinusoidal adalah:
V(t) = Vm sin(ωt)
Kemudian membandingkan ini untuk ekspresi kita diberikan untuk bentuk gelombang sinusoidal atas Vm = 169,8 sin (377t) akan memberi kita nilai tegangan puncak 169,8 volt untuk gelombang.
Tegangan RMS bentuk gelombang dihitung sebagai:
V(rms) = 0.707 x Nilai puncak maksimum
V(rms) = 0.707 x 169.8 = 120 volts
Kecepatan sudut (ω) diberikan sebagai 377 rad/s. Kemudian 2πƒ = 377. Jadi frekuensi gelombang dihitung sebagai:

Nilai tegangan Vi sesaat setelah 6 mS diberikan sebagai:
V(i) = Vm sin (ωt)
V(i) = 169.8 sin (377 x 0.006)
V(i) = 169.8 sin (2.262 rad)
Sudut dalam derajat nilai tegangan sesaat karena itu diberikan sebagai:


Dalam tutorial berikutnya tentang Rangkaian AC kita akan melihat Pergeseran Fasa atau Beda Fasa (Phase Difference) yaitu hubungan antara dua bentuk gelombang sinusoidal yang memiliki frekuensi yang sama tetapi melewati sumbu nol horizontal pada interval waktu yang berbeda.
Dari sini kita dapat melihat bahwa ada hubungan antara Listrik dan Magnet, ketika Michael Faraday menemukan efek "Induksi Elektromagnetik". Dan prinsip dasar inilah yang digunakan mesin dan generator listrik untuk menghasilkan Gelombang Sinusoidal untuk pasokan listrik utama kita.
Dalam tutorial Induksi Elektromagnetik, kami mengatakan bahwa ketika konduktor kawat tunggal bergerak melalui medan magnet permanen sehingga memotong garis fluksnya, GGL diinduksi di dalamnya.

Namun, jika konduktor bergerak secara paralel dengan medan magnet dalam kasus titik A dan B, tidak ada garis fluks yang terpotong dan tidak ada GGL (Gaya Gerak Listrik) yang diinduksi ke dalam konduktor.
Tetapi jika konduktor bergerak pada sudut kanan ke medan magnet seperti pada kasus titik C dan D , jumlah maksimum fluks magnetik dipotong menghasilkan jumlah maksimum GGL terinduksi.
Juga, ketika konduktor memotong medan magnet pada sudut yang berbeda antara titik A dan C, 0 dan 90° jumlah GGL terinduksi akan terletak di suatu tempat antara nol dan nilai maksimum ini.
Kemudian jumlah ggl yang diinduksi dalam konduktor tergantung pada sudut antara konduktor dan fluks magnet serta kekuatan medan magnet.
Generator AC menggunakan prinsip induksi elektromagnetik Faraday untuk mengubah energi mekanik seperti rotasi, menjadi energi listrik, gelombang sinusoidal.
Generator sederhana terdiri dari sepasang magnet permanen yang menghasilkan medan magnet tetap antara kutub utara dan selatan.
Di dalam medan magnet ini ada satu lingkaran persegi panjang kawat yang dapat diputar di sekitar sumbu tetap yang memungkinkannya memotong fluks magnet pada berbagai sudut seperti ditunjukkan di bawah ini.
Dasar Generator AC Single Coil

Ketika kumparan berputar berlawanan arah jarum jam di sekitar sumbu pusat yang tegak lurus terhadap medan magnet, loop kawat memotong garis-garis gaya magnet yang diatur antara kutub utara dan selatan pada sudut yang berbeda saat loop berputar. Jumlah GGL terinduksi dalam loop pada setiap saat waktu sebanding dengan sudut rotasi loop kawat.
Saat loop kawat ini berputar, elektron-elektron dalam kawat mengalir dalam satu arah di sekitar loop. Sekarang ketika loop kawat telah diputar melewati 180° titik dan bergerak di garis gaya magnetik dalam arah yang berlawanan, elektron dalam kawat perubahan lingkaran dan mengalir dalam arah yang berlawanan. Kemudian arah gerakan elektron menentukan polaritas tegangan yang diinduksi.
Jadi kita dapat melihat bahwa ketika loop atau kumparan secara fisik memutar satu putaran penuh, atau 360°, satu gelombang sinusoidal penuh diproduksi dengan satu siklus bentuk gelombang yang diproduksi untuk setiap putaran kumparan.
Ketika kumparan berputar di dalam medan magnet, sambungan listrik dibuat ke kumparan dengan menggunakan sikat karbon dan cincin selip yang digunakan untuk mentransfer arus listrik yang diinduksi dalam kumparan.
Jumlah GGL yang diinduksi ke dalam kumparan memotong garis gaya magnet ditentukan oleh tiga faktor berikut.
- Kecepatan - kecepatan putaran coil di dalam medan magnet.
- Kekuatan - kekuatan medan magnet.
- Panjang - panjang coil atau konduktor yang melewati medan magnet.
Karena satu siklus ggl (gaya gerak listrik) yang diinduksi diproduksi setiap putaran penuh kumparan melalui medan magnet yang terdiri dari kutub utara dan selatan seperti yang ditunjukkan di atas.
Jika kumparan berputar pada kecepatan konstan, jumlah siklus yang konstan akan dihasilkan per detik memberikan konstanta frekuensi.
Jadi dengan meningkatkan kecepatan putaran kumparan, frekuensi juga akan meningkat. Oleh karena itu, frekuensi sebanding dengan kecepatan rotasi, ( ƒ ∝ Ν ) di mana Ν = r.p.m
Selain itu, generator kumparan tunggal kami yang sederhana di atas hanya memiliki dua kutub, satu kutub utara dan satu kutub selatan, yang hanya memberikan satu pasang kutub.
Jika kita menambahkan lebih banyak kutub magnet pada generator di atas sehingga sekarang memiliki empat kutub total, dua utara dan dua selatan, maka untuk setiap putaran kumparan, dua siklus akan diproduksi untuk kecepatan rotasi yang sama.
Oleh karena itu, frekuensi sebanding dengan jumlah pasangan kutub magnet, ( ƒ ∝ P ) dari generator di mana P = jumlah "pasangan kutub".
Kemudian dari dua fakta ini kita dapat mengatakan bahwa output frekuensi dari generator AC adalah:
frekuensi generator
f α N, dan f α P
∴ f = N x P di siklus/min
sebagai Frekuensi diukur di Hertz

Di mana: Ν adalah kecepatan rotasi dalam r.p.m. P adalah jumlah "pasang kutub" dan 60 mengubahnya menjadi detik.
Tegangan Sesaat
GGL (Gaya Gerak Listrik) yang diinduksi dalam coil kapan saja tergantung pada kecepatan atau kecepatan kumparan memotong garis fluks magnet antara kutub dan ini tergantung pada sudut rotasi, Theta ( θ ) dari perangkat pembangkit.Karena bentuk gelombang AC secara konstan mengubah nilainya atau amplitudo, bentuk gelombang pada saat kapan saja akan memiliki nilai yang berbeda dari gelombang berikutnya.
Misalnya, nilai pada 1ms akan berbeda dengan nilai pada 1.2 ms dan seterusnya. Nilai-nilai ini umumnya dikenal sebagai Nilai Instan, atau Vi.
Kemudian nilai sesaat dari bentuk gelombang dan juga arahnya akan bervariasi sesuai dengan posisi kumparan dalam medan magnet seperti yang ditunjukkan di bawah ini.
Pemindahan Coil di dalam Medan Magnet

Nilai sesaat dari bentuk gelombang sinusoidal diberikan sebagai "Nilai sesaat = Nilai maksimum x sin θ" dan ini digeneralisasi oleh rumus.
Vi = Vmax x sinθ
Dimana, Vmax adalah tegangan maksimum diinduksi dalam kumparan dan θ = ωt, adalah sudut rotasi dari kumparan terhadap waktu. Jika kita mengetahui nilai maksimum atau puncak gelombang, dengan menggunakan rumus di atas nilai sesaat di berbagai titik di sepanjang gelombang dapat dihitung.
Dengan memplot nilai-nilai ini ke kertas grafik, bentuk gelombang sinusoidal dapat dibangun. Untuk mempermudah, kami akan memplot nilai sesaat untuk bentuk gelombang sinusoidal pada setiap 45° rotasi memberi kita 8 poin untuk plot.
Sekali lagi, untuk membuatnya tetap sederhana, kita akan mengasumsikan tegangan maksimum, nilai Vmax 100V.
Merencanakan nilai sesaat pada interval yang lebih pendek, misalnya pada setiap 30° (12 titik) atau 10° (36 titik) misalnya akan menghasilkan konstruksi gelombang sinusoidal yang lebih akurat.
Konstruksi Bentuk Sinusoidal
Sudut Coil ( θ )
|
0
|
45
|
90
|
135
|
180
|
225
|
270
|
315
|
360
|
e = Vmax.sinθ
|
0
|
70.71
|
100
|
70.71
|
0
|
-70.71
|
-100
|
-70.71
|
-0
|

Titik-titik pada gelombang sinusoidal diperoleh dengan memproyeksikan seberang berbagai posisi rotasi antara 0° dan 360° ke ordinat dari bentuk gelombang yang sesuai dengan sudut, θ dan ketika kawat loop atau kumparan berputar satu putaran penuh, atau 360°, satu bentuk gelombang penuh diproduksi.
Dari plot bentuk gelombang sinusoidal kita dapat melihat bahwa ketika θ sama dengan 0°, 180° atau 360°, yang dihasilkan GGL adalah nol sebagai kumparan memotong jumlah minimum garis fluks.
Tetapi ketika θ sama dengan 90° dan 270° GGL yang dihasilkan berada pada nilai maksimumnya ketika jumlah fluks maksimum dipotong.
Oleh karena itu bentuk gelombang sinusoidal memiliki puncak positif pada 90° dan puncak negatif pada 270°. Posisi B, D, F dan H menghasilkan nilai GGL yang sesuai dengan rumus: e = Vmax.sinθ .
Kemudian bentuk gelombang yang dihasilkan oleh generator loop tunggal sederhana kami biasanya disebut sebagai Gelombang Sinus karena dikatakan berbentuk sinusoidal.
Jenis gelombang ini disebut gelombang sinus karena didasarkan pada fungsi sinus trigonometri yang digunakan dalam matematika, ( x (t) = Amax.sinθ ).
Ketika berhadapan dengan gelombang sinus dalam domain waktu dan khususnya gelombang sinus terkait saat ini, unit pengukuran yang digunakan sepanjang sumbu horizontal dari bentuk gelombang dapat berupa waktu, derajat atau radian.
Dalam teknik elektro, lebih umum menggunakan Radian sebagai pengukuran sudut sudut sepanjang sumbu horizontal daripada derajat.
Misalnya, ω = 100 rad/s, atau 500 rad/s.
Radian
Radian, (rad) didefinisikan secara matematis sebagai kuadran lingkaran di mana jarak subtended pada keliling lingkaran adalah sama dengan panjang dari jari-jari ( r ) dari lingkaran yang sama.Karena keliling lingkaran sama dengan 2π radius x , harus ada 2π radian sekitar 360° lingkaran.
Dengan kata lain, radian adalah satuan pengukuran sudut dan panjang satu radian (r) akan sesuai dengan 6,284 (2*π) kali di sekitar seluruh lingkaran.
Jadi satu radian sama dengan 360°/2π = 57,3°. Dalam teknik elektro, penggunaan radian sangat umum sehingga penting untuk mengingat rumus berikut.
Definisi Radian

2π rad = 360°
∴ 1rad = 57.3°
Kemudian setengah bentuk gelombang sinusoidal harus sama dengan 1π radian atau hanya π (pi). Maka mengetahui bahwa pi, ( π ) sama dengan 3.142, hubungan antara derajat dan radian untuk bentuk gelombang sinusoidal diberikan sebagai:
Hubungan antara Derajat dan Radian

Menerapkan dua persamaan ini ke berbagai titik di sepanjang bentuk gelombang memberi kita.

Konversi antara derajat dan radian untuk persamaan yang lebih umum digunakan dalam analisis sinusoidal diberikan dalam tabel berikut.
Tabel Hubungan antara Derajat dan Radian

Kecepatan di mana generator berputar di sekitar poros pusatnya menentukan frekuensi gelombang sinusoidal. Karena frekuensi bentuk gelombang diberikan sebagai ƒ Hz atau siklus per detik, bentuk gelombang juga memiliki frekuensi sudut, ω, (huruf Yunani omega), dalam radian per detik.
Kemudian kecepatan sudut dari bentuk gelombang sinusoidal diberikan sebagai.
Kecepatan Sudut Gelombang Sinusoidal
ω = 2πf (rad/sec)Contoh Gelombang Sinusoidal No.1
Sebuah gelombang sinusoidal didefinisikan sebagai: Vm = 169,8 sin (377t) volt. Hitung tegangan RMS dari bentuk gelombang, frekuensinya, dan nilai tegangan sesaat, (Vi) setelah enam milidetik (6 ms).Kita tahu dari atas bahwa ekspresi umum yang diberikan untuk bentuk gelombang sinusoidal adalah:
V(t) = Vm sin(ωt)
Kemudian membandingkan ini untuk ekspresi kita diberikan untuk bentuk gelombang sinusoidal atas Vm = 169,8 sin (377t) akan memberi kita nilai tegangan puncak 169,8 volt untuk gelombang.
Tegangan RMS bentuk gelombang dihitung sebagai:
V(rms) = 0.707 x Nilai puncak maksimum
V(rms) = 0.707 x 169.8 = 120 volts
Kecepatan sudut (ω) diberikan sebagai 377 rad/s. Kemudian 2πƒ = 377. Jadi frekuensi gelombang dihitung sebagai:

Nilai tegangan Vi sesaat setelah 6 mS diberikan sebagai:
V(i) = Vm sin (ωt)
V(i) = 169.8 sin (377 x 0.006)
V(i) = 169.8 sin (2.262 rad)
2.262 rad x 57.3° = 129.6°
V(i) = 169.8 sin (129.6°) = 169.8 x 0.771
∴ V(i) = 130.8 Tegangan puncak
Perhatikan bahwa kecepatan sudut pada waktu t = 6mS diberikan dalam radian (rad). Kita bisa, jika diinginkan, mengubahnya menjadi sudut yang setara dalam derajat dan menggunakan nilai ini sebagai gantinya untuk menghitung nilai tegangan sesaat.Sudut dalam derajat nilai tegangan sesaat karena itu diberikan sebagai:

Menghitung Nilai Gelombang Sinusoidal
Kemudian format umum yang digunakan untuk menganalisis dan menghitung berbagai nilai Gelombang Sinusoid adalah sebagai berikut:Gelombang Sinusoidal

Dalam tutorial berikutnya tentang Rangkaian AC kita akan melihat Pergeseran Fasa atau Beda Fasa (Phase Difference) yaitu hubungan antara dua bentuk gelombang sinusoidal yang memiliki frekuensi yang sama tetapi melewati sumbu nol horizontal pada interval waktu yang berbeda.