Rangkaian RLC Paralel
Rangkaian RLC Paralel adalah kebalikan dari Rangkaian RLC Seri yang kita lihat di tutorial sebelumnya meskipun beberapa konsep sebelumnya dan persamaan masih berlaku.
Namun, analisis rangkaian RLC paralel dapat sedikit lebih sulit secara matematis daripada rangkaian RLC seri sehingga dalam tutorial ini tentang rangkaian RLC paralel hanya komponen murni yang diasumsikan untuk menjaga hal-hal sederhana. Kali ini alih-alih arus menjadi umum untuk komponen rangkaian, tegangan yang diberikan sekarang umum untuk semua sehingga kita perlu menemukan arus cabang individu melalui masing-masing elemen.
Impedansi total, Z dari rangkaian RLC paralel dihitung menggunakan arus rangkaian yang sama dengan rangkaian DC paralel, perbedaan kali ini adalah bahwa penerimaan (admitansi) digunakan sebagai pengganti impedansi. Pertimbangkan rangkaian RLC paralel di bawah ini.
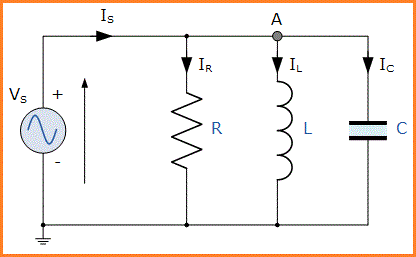
Dalam rangkaian RLC paralel di atas, kita dapat melihat bahwa tegangan supply,VS adalah umum untuk ketiga komponen sedangkan arus supply IS terdiri dari tiga bagian. Arus yang mengalir melalui resistor, IR, arus yang mengalir melalui induktor, IL dan arus yang melalui kapasitor, IC. Tapi arus yang mengalir melalui setiap cabang dan karena itu masing-masing komponen akan berbeda satu sama lain dan dengan arus supply, IS.
Total arus yang ditarik dari supply tidak akan menjadi jumlah matematis dari tiga arus cabang individu tetapi jumlah vektornya. Seperti rangkaian RLC seri, kita dapat menyelesaikan rangkaian ini menggunakan metode fasor atau vektor tetapi kali ini diagram vektor akan memiliki tegangan sebagai rujukannya dengan tiga vektor arus yang diplot sehubungan dengan tegangan.
Diagram fasor untuk rangkaian RLC paralel dihasilkan dengan menggabungkan bersama-sama tiga fasor individu untuk setiap komponen dan menambahkan arus secara vektor. Karena tegangan melintasi rangkaian adalah umum untuk ketiga elemen rangkaian, kita dapat menggunakan ini sebagai vektor referensi dengan tiga vektor arus digambar relatif terhadap ini pada sudut yang sesuai.
Vektor IS yang dihasilkan diperoleh dengan menambahkan bersama-sama dua vektor, IL dan IC dan kemudian menambahkan jumlah ini ke vektor IR yang tersisa. Sudut yang dihasilkan diperoleh antara V dan IS akan menjadi sudut fase rangkaian seperti yang ditunjukkan di bawah ini.
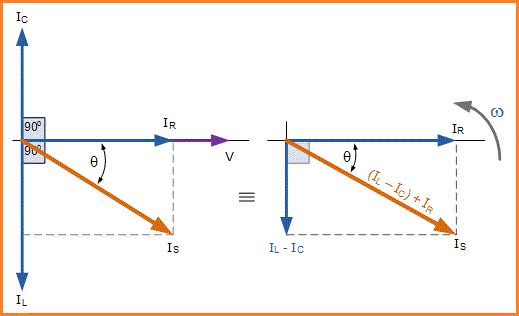
Kita dapat melihat dari diagram fasor di sisi kanan atas bahwa vektor arus menghasilkan segitiga persegi panjang, terdiri dari sisi miring IS, sumbu horizontal IR dan sumbu vertikal IL- IC Semoga Anda akan memahami kemudian, bahwa ini membentuk sebuah Arus Segitiga.
Dan oleh karena itu kita dapat menggunakan teorema Pythagoras pada segitiga ini untuk secara matematis memperoleh besarnya arus cabang sepanjang sumbu x dan sumbu y dan kemudian menentukan arus total IS dari komponen-komponen ini seperti yang ditunjukkan.
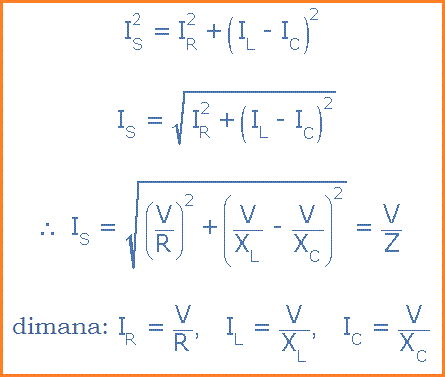
Karena tegangan melintasi rangkaian adalah umum untuk ketiga elemen rangkaian, arus melalui masing-masing cabang dapat ditemukan menggunakan Hukum Kirchoff 1 - Arus, (KCL).
Hukum Arus Kirchoff ini atau hukum persimpangan/junction menyatakan bahwa "arus total yang memasuki persimpangan atau simpul persis sama dengan arus yang meninggalkan simpul itu", sehingga arus yang masuk dan meninggalkan simpul "A" di atas dirumuskan sebagai:
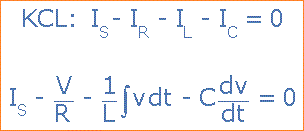
Mengambil turunannya, membaginya melalui persamaan di atas dengan C dan mengatur ulang memberi kita persamaan Orde-2 Dua berikut untuk arus rangkaian. Ini menjadi persamaan orde-2 karena ada dua elemen reaktif dalam rangkaian, induktor dan kapasitor.
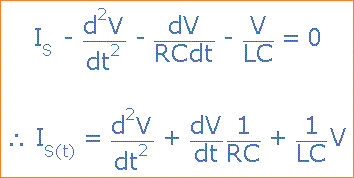
Perlawanan terhadap aliran arus dalam jenis rangkaian AC terdiri dari tiga komponen: XL, XC dan R dengan kombinasi tiga nilai tersebut memberikan impedansi rangkaian, Z.
Kita tahu dari atas bahwa tegangan memiliki amplitudo dan fase yang sama di semua komponen rangkaian RLC paralel. Kemudian impedansi di setiap komponen juga dapat dijelaskan secara matematis sesuai dengan arus yang mengalir, dan tegangan pada masing-masing elemen.

Anda akan melihat bahwa persamaan akhir untuk rangkaian RLC paralel menghasilkan impedansi kompleks untuk setiap cabang paralel karena setiap elemen menjadi kebalikan dari impedansi, (1/Z) dengan kebalikan dari impedansi yang disebut Penerimaan/admitansi (Admittance).
Dalam rangkaian AC paralel, lebih mudah untuk menggunakan Admitansi, simbol ( Y ) untuk menyelesaikan impedansi cabang kompleks terutama ketika dua atau lebih impedansi cabang paralel yang terlibat (membantu dengan matematika). Admitansi total rangkaian hanya dapat ditemukan dengan penambahan admitansi paralel. Kemudian impedansi total, ZT dari rangkaian karena itu akan menjadi 1/YT Siemens seperti yang ditunjukkan.

Unit baru untuk admitansi adalah Siemens, disingkat S, (simbol lama mho ℧, ohm terbalik). Admitansi ditambahkan bersama dalam cabang paralel, sedangkan impedansi ditambahkan bersama dalam cabang seri. Tetapi jika kita dapat memiliki timbal balik dari impedansi, kami juga dapat memiliki timbal balik resistansi dan reaktansi sebagai impedansi terdiri dari dua komponen, R dan X. Kemudian timbal-balik dari resistansi disebut Konduktansi dan timbal-balik dari reaktansi disebut Susceptansi.

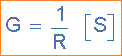

Karena itu kita dapat mendefinisikan susceptance induktif dan kapasitif sebagai:
BL = B∠-90° = 0-jB dan BC = B∠+90° = 0+jB
Dalam rangkaian AC seri resistansi terhadap aliran arus adalah impedansi, Z yang memiliki dua komponen, resistansi R dan reaktansi, X dan dari dua komponen ini kita dapat membuat segitiga impedansi. Demikian pula, dalam rangkaian RLC paralel, admitansi, Y juga memiliki dua komponen, konduktansi, G dan susceptanSI, B. Hal ini memungkinkan untuk membuat segitiga admitansi yang memiliki sumbu konduktansi horisontal, G dan sumbu susceptance vertikal, jB seperti yang ditunjukkan.

Sekarang kita memiliki segitiga admitansi, kita dapat menggunakan Pythagoras untuk menghitung besaran ketiga sisi serta sudut fasa seperti yang ditunjukkan.
dari Pythagoras
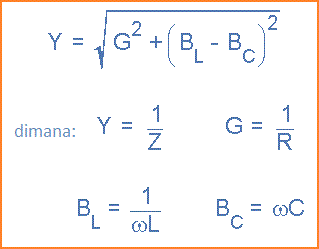
Kemudian kita dapat mendefinisikan admitansi rangkaian dan impedansi sehubungan dengan admitansi sebagai:

Memberi kami sudut faktor daya:
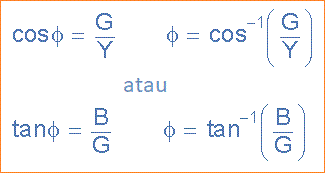
Sebagai admitansi, Y dari rangkaian RLC paralel adalah jumlah yang kompleks, admitansi yang sesuai dengan bentuk umum impedansi Z = R + jX untuk rangkaian seri akan ditulis sebagai Y = G - jB untuk rangkaian paralel di mana bagian nyata G adalah konduktansi dan bagian imajiner jB adalah susceptance. Dalam bentuk kutub ini akan dirumuskan sebagai:

Reaktansi Induktif, (XL):
XL = ωL = 2πfL = 2π.60.142x10-3 = 53.54Ω
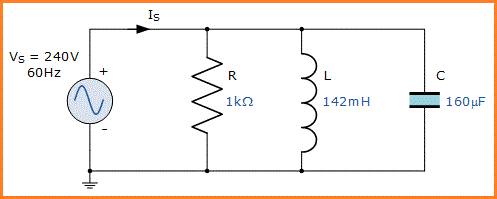
Rekatansi Kapasitif, (XC):
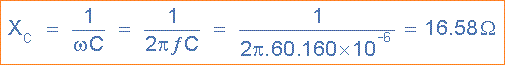
Impedansi, (Z):
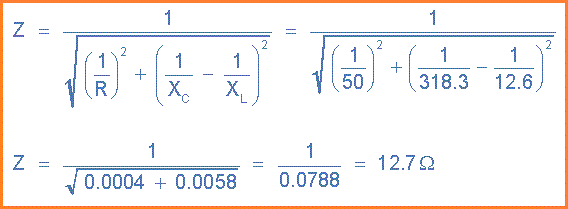
Arus Supply, (Is):

Rangkaian RLC paralel

1). Reaktansi Induktif, ( XL ):
XL = ωL = 2πfL = 2π.100.0.02x10 = 12.6Ω
2). Reaktansi Kapasitif, ( XC ):

3). Impedansi, ( Z ):
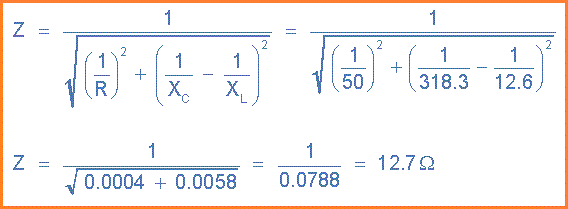
4). Arus melalui resistor, R ( IR ):
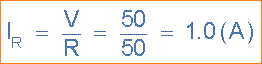
5). Arus melalui induktor, L ( IR ):

6). Arus melalui kapasitor, C ( IC ):

7). Total supply arus, ( IS ):

8). Konduktansi, ( G ):
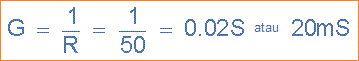
9). Induktif Susceptansi, ( BL ):
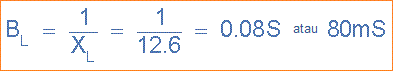
10). Kapasitif Susceptansi, ( BC ):

11). Admitansi, ( Y ):

12). Sudut Fasa, ( φ ) antara arus yang dihasilkan dan tegangan supply:


Jaringan RLC paralel dapat dianalisis menggunakan diagram vektor seperti halnya dengan rangkaian RLC seri. Namun, analisis rangkaian RLC paralel sedikit lebih sulit secara matematis daripada untuk rangkaian RLC seri ketika mengandung dua atau lebih cabang arus. Jadi rangkaian AC paralel dapat dengan mudah dianalisis menggunakan kebalikan dari impedansi yang disebut Admitansi.
Admitansi adalah kebalikan dari impedansi diberikan simbol, Y. Seperti halnya impedansi, itu adalah kuantitas kompleks yang terdiri dari bagian nyata dan bagian imajiner.
Bagian nyata adalah kebalikan dari resistansi dan disebut Konduktansi, simbol Y, sedangkan bagian imajiner adalah kebalikan dari reaktansi dan disebut Susceptance, simbol B dan dinyatakan dalam bentuk kompleks sebagai: Y = G + jB dengan dualitas antara dua kompleks impedansi didefinisikan sebagai:
Karena susceptance adalah kebalikan dari reaktansi, dalam rangkaian induktif, susceptance induktif, BL akan bernilai negatif dan dalam rangkaian kapasitif, kapasitif susceptance, BL akan bernilai positif. Yang tepat berlawanan dengan XL dan XC masing-masing.
Kita telah melihat sejauh ini bahwa rangkaian RLC seri dan paralel mengandung reaktansi kapasitif dan reaktansi induktif dalam rangkaian yang sama. Jika kita bervariasi frekuensi di rangkaian ini ada harus menjadi titik dimana nilai reaktansi kapasitif sama bahwa dari reaktansi induktif dan oleh karena itu, XL dan XC. Titik frekuensi di mana hal ini terjadi disebut resonansi dan dalam tutorial berikutnya kita akan melihat Resonansi Seri dan bagaimana kehadirannya mengubah karakteristik rangkaian.
Namun, analisis rangkaian RLC paralel dapat sedikit lebih sulit secara matematis daripada rangkaian RLC seri sehingga dalam tutorial ini tentang rangkaian RLC paralel hanya komponen murni yang diasumsikan untuk menjaga hal-hal sederhana. Kali ini alih-alih arus menjadi umum untuk komponen rangkaian, tegangan yang diberikan sekarang umum untuk semua sehingga kita perlu menemukan arus cabang individu melalui masing-masing elemen.
Impedansi total, Z dari rangkaian RLC paralel dihitung menggunakan arus rangkaian yang sama dengan rangkaian DC paralel, perbedaan kali ini adalah bahwa penerimaan (admitansi) digunakan sebagai pengganti impedansi. Pertimbangkan rangkaian RLC paralel di bawah ini.
Rangkaian RLC Paralel

Dalam rangkaian RLC paralel di atas, kita dapat melihat bahwa tegangan supply,VS adalah umum untuk ketiga komponen sedangkan arus supply IS terdiri dari tiga bagian. Arus yang mengalir melalui resistor, IR, arus yang mengalir melalui induktor, IL dan arus yang melalui kapasitor, IC. Tapi arus yang mengalir melalui setiap cabang dan karena itu masing-masing komponen akan berbeda satu sama lain dan dengan arus supply, IS.
Total arus yang ditarik dari supply tidak akan menjadi jumlah matematis dari tiga arus cabang individu tetapi jumlah vektornya. Seperti rangkaian RLC seri, kita dapat menyelesaikan rangkaian ini menggunakan metode fasor atau vektor tetapi kali ini diagram vektor akan memiliki tegangan sebagai rujukannya dengan tiga vektor arus yang diplot sehubungan dengan tegangan.
Diagram fasor untuk rangkaian RLC paralel dihasilkan dengan menggabungkan bersama-sama tiga fasor individu untuk setiap komponen dan menambahkan arus secara vektor. Karena tegangan melintasi rangkaian adalah umum untuk ketiga elemen rangkaian, kita dapat menggunakan ini sebagai vektor referensi dengan tiga vektor arus digambar relatif terhadap ini pada sudut yang sesuai.
Vektor IS yang dihasilkan diperoleh dengan menambahkan bersama-sama dua vektor, IL dan IC dan kemudian menambahkan jumlah ini ke vektor IR yang tersisa. Sudut yang dihasilkan diperoleh antara V dan IS akan menjadi sudut fase rangkaian seperti yang ditunjukkan di bawah ini.
Diagram Fasor untuk Rangkaian RLC Paralel

Kita dapat melihat dari diagram fasor di sisi kanan atas bahwa vektor arus menghasilkan segitiga persegi panjang, terdiri dari sisi miring IS, sumbu horizontal IR dan sumbu vertikal IL- IC Semoga Anda akan memahami kemudian, bahwa ini membentuk sebuah Arus Segitiga.
Dan oleh karena itu kita dapat menggunakan teorema Pythagoras pada segitiga ini untuk secara matematis memperoleh besarnya arus cabang sepanjang sumbu x dan sumbu y dan kemudian menentukan arus total IS dari komponen-komponen ini seperti yang ditunjukkan.
Arus Segitiga untuk Rangkaian RLC Paralel
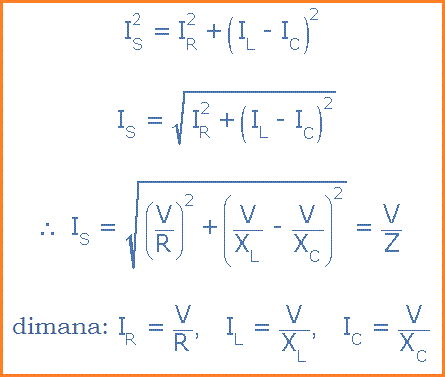
Karena tegangan melintasi rangkaian adalah umum untuk ketiga elemen rangkaian, arus melalui masing-masing cabang dapat ditemukan menggunakan Hukum Kirchoff 1 - Arus, (KCL).
Hukum Arus Kirchoff ini atau hukum persimpangan/junction menyatakan bahwa "arus total yang memasuki persimpangan atau simpul persis sama dengan arus yang meninggalkan simpul itu", sehingga arus yang masuk dan meninggalkan simpul "A" di atas dirumuskan sebagai:
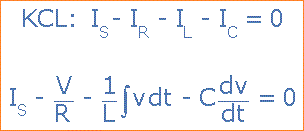
Mengambil turunannya, membaginya melalui persamaan di atas dengan C dan mengatur ulang memberi kita persamaan Orde-2 Dua berikut untuk arus rangkaian. Ini menjadi persamaan orde-2 karena ada dua elemen reaktif dalam rangkaian, induktor dan kapasitor.
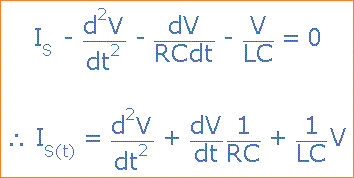
Perlawanan terhadap aliran arus dalam jenis rangkaian AC terdiri dari tiga komponen: XL, XC dan R dengan kombinasi tiga nilai tersebut memberikan impedansi rangkaian, Z.
Kita tahu dari atas bahwa tegangan memiliki amplitudo dan fase yang sama di semua komponen rangkaian RLC paralel. Kemudian impedansi di setiap komponen juga dapat dijelaskan secara matematis sesuai dengan arus yang mengalir, dan tegangan pada masing-masing elemen.
Impedansi Rangkaian RLC Paralel

Anda akan melihat bahwa persamaan akhir untuk rangkaian RLC paralel menghasilkan impedansi kompleks untuk setiap cabang paralel karena setiap elemen menjadi kebalikan dari impedansi, (1/Z) dengan kebalikan dari impedansi yang disebut Penerimaan/admitansi (Admittance).
Dalam rangkaian AC paralel, lebih mudah untuk menggunakan Admitansi, simbol ( Y ) untuk menyelesaikan impedansi cabang kompleks terutama ketika dua atau lebih impedansi cabang paralel yang terlibat (membantu dengan matematika). Admitansi total rangkaian hanya dapat ditemukan dengan penambahan admitansi paralel. Kemudian impedansi total, ZT dari rangkaian karena itu akan menjadi 1/YT Siemens seperti yang ditunjukkan.
Admitansi pada Rangkaian RLC Paralel

Unit baru untuk admitansi adalah Siemens, disingkat S, (simbol lama mho ℧, ohm terbalik). Admitansi ditambahkan bersama dalam cabang paralel, sedangkan impedansi ditambahkan bersama dalam cabang seri. Tetapi jika kita dapat memiliki timbal balik dari impedansi, kami juga dapat memiliki timbal balik resistansi dan reaktansi sebagai impedansi terdiri dari dua komponen, R dan X. Kemudian timbal-balik dari resistansi disebut Konduktansi dan timbal-balik dari reaktansi disebut Susceptansi.
Konduktansi, Admitansi, dan Susceptansi
Unit yang digunakan untuk konduktansi, admitansi dan susceptansi semuanya sama yaitu Siemens (S), yang juga dapat dianggap sebagai kebalikan dari Ohm atau ohmm-1, tetapi simbol yang digunakan untuk setiap elemen berbeda dan dalam komponen murni ini diberikan sebagai:Admitansi(Y):
Admitansi adalah kebalikan dari impedansi, Z dan diberi simbol Y. Dalam rangkaian AC, admitansi didefinisikan sebagai kemudahan di mana rangkaian yang terdiri dari resistansi dan reaktansi memungkinkan arus mengalir ketika tegangan diterapkan dengan mempertimbangkan perbedaan fasa antara tegangan dan arus. Admitansi dari rangkaian paralel adalah rasio arus fasor ke tegangan fasor dengan sudut admitansi menjadi negatif terhadap impedansi.
Konduktansi (G):
Konduktansi adalah kebalikan dari resistansi, R dan diberikan simbol G. Konduktansi didefinisikan sebagai kemudahan di mana resistor (atau serangkaian resistor) memungkinkan arus mengalir ketika tegangan, baik AC atau DC diterapkan.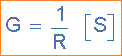
Susceptansi (B):
Susceptansi adalah kebalikan dari dari reaktansi murni, X dan diberi simbol B. Dalam rangkaian AC, susceptansi didefinisikan sebagai kemudahan reaktansi (atau serangkaian reaktansi) memungkinkan arus bolak-balik mengalir ketika tegangan frekuensi tertentu diberikan. Susceptance memiliki tanda berlawanan dengan reaktansi sehingga Kapasitif susceptansi BC positif, (ve) nilai sementara induktif susceptance BL negatif, (-ve) nilai.
Karena itu kita dapat mendefinisikan susceptance induktif dan kapasitif sebagai:
BL = B∠-90° = 0-jB dan BC = B∠+90° = 0+jB
Dalam rangkaian AC seri resistansi terhadap aliran arus adalah impedansi, Z yang memiliki dua komponen, resistansi R dan reaktansi, X dan dari dua komponen ini kita dapat membuat segitiga impedansi. Demikian pula, dalam rangkaian RLC paralel, admitansi, Y juga memiliki dua komponen, konduktansi, G dan susceptanSI, B. Hal ini memungkinkan untuk membuat segitiga admitansi yang memiliki sumbu konduktansi horisontal, G dan sumbu susceptance vertikal, jB seperti yang ditunjukkan.
Admitansi Segitiga untuk Rangkaian RLC Paralel

Sekarang kita memiliki segitiga admitansi, kita dapat menggunakan Pythagoras untuk menghitung besaran ketiga sisi serta sudut fasa seperti yang ditunjukkan.
dari Pythagoras
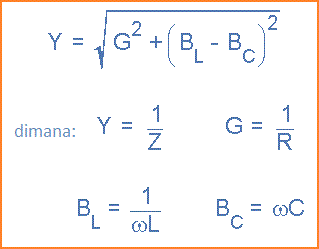
Kemudian kita dapat mendefinisikan admitansi rangkaian dan impedansi sehubungan dengan admitansi sebagai:

Memberi kami sudut faktor daya:
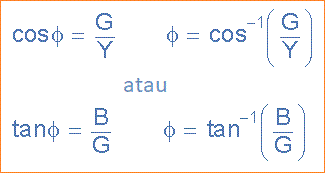
Sebagai admitansi, Y dari rangkaian RLC paralel adalah jumlah yang kompleks, admitansi yang sesuai dengan bentuk umum impedansi Z = R + jX untuk rangkaian seri akan ditulis sebagai Y = G - jB untuk rangkaian paralel di mana bagian nyata G adalah konduktansi dan bagian imajiner jB adalah susceptance. Dalam bentuk kutub ini akan dirumuskan sebagai:

Contoh: Rangkaian RLC Paralel No.1
Sebuah resistor 1kΩ, sebuah coil 142mH dan kapasitor 160uF semua terhubung secara paralel melintasi 240V, supply 60Hz. Hitung impedansi dari rangkaian RLC paralel dan arus yang diambil dari supply.
Impedansi Rangkaian RLC Paralel
Dalam rangkaian AC, resistor tidak terpengaruh oleh frekuensi karena itu R = 1kΩReaktansi Induktif, (XL):
XL = ωL = 2πfL = 2π.60.142x10-3 = 53.54Ω
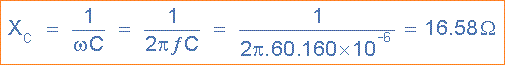
Impedansi, (Z):
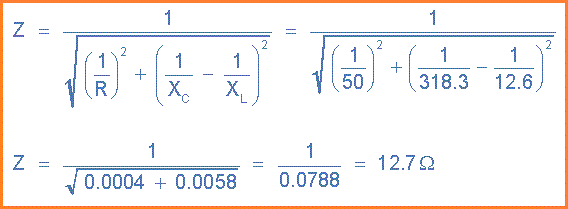
Arus Supply, (Is):

Contoh: Rangkaian Paralel RLC No.2
Sebuah resistor 50Ω, sebuah coil 20mH dan kapasitor 5uF semua terhubung secara paralel di sebuah 50V, supply 100Hz. Hitung total arus yang diambil dari supply, arus untuk setiap cabang, total impedansi dari rangkaian dan sudut fasa. Juga buat segitiga arus dan admitansi yang mewakili rangkaian.Rangkaian RLC paralel

1). Reaktansi Induktif, ( XL ):
XL = ωL = 2πfL = 2π.100.0.02x10 = 12.6Ω
2). Reaktansi Kapasitif, ( XC ):

3). Impedansi, ( Z ):
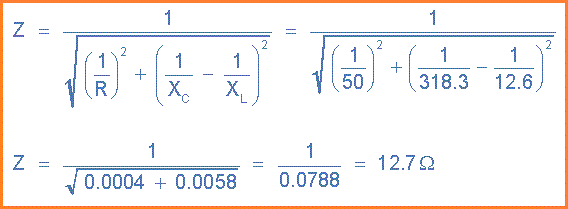
4). Arus melalui resistor, R ( IR ):
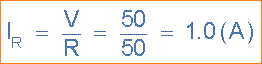
5). Arus melalui induktor, L ( IR ):

6). Arus melalui kapasitor, C ( IC ):

7). Total supply arus, ( IS ):

8). Konduktansi, ( G ):
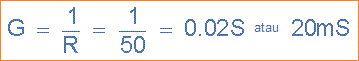
9). Induktif Susceptansi, ( BL ):
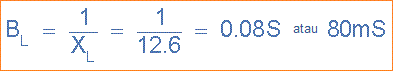
10). Kapasitif Susceptansi, ( BC ):

11). Admitansi, ( Y ):

12). Sudut Fasa, ( φ ) antara arus yang dihasilkan dan tegangan supply:

Arus dan Segitiga Admitansi

Ringkasan Rangkaian RLC paralel
Dalam rangkaian RLC paralel yang berisi Resistor, Induktor dan Kapasitor, arus rangkaian IS adalah jumlah fasor yang terdiri dari tiga komponen, IR, IL dan IC dengan tegangan supply yang umum untuk ketiganya. Karena tegangan supply umum untuk ketiga komponen itu digunakan sebagai referensi horisontal ketika membangun segitiga arus.Jaringan RLC paralel dapat dianalisis menggunakan diagram vektor seperti halnya dengan rangkaian RLC seri. Namun, analisis rangkaian RLC paralel sedikit lebih sulit secara matematis daripada untuk rangkaian RLC seri ketika mengandung dua atau lebih cabang arus. Jadi rangkaian AC paralel dapat dengan mudah dianalisis menggunakan kebalikan dari impedansi yang disebut Admitansi.
Admitansi adalah kebalikan dari impedansi diberikan simbol, Y. Seperti halnya impedansi, itu adalah kuantitas kompleks yang terdiri dari bagian nyata dan bagian imajiner.
Bagian nyata adalah kebalikan dari resistansi dan disebut Konduktansi, simbol Y, sedangkan bagian imajiner adalah kebalikan dari reaktansi dan disebut Susceptance, simbol B dan dinyatakan dalam bentuk kompleks sebagai: Y = G + jB dengan dualitas antara dua kompleks impedansi didefinisikan sebagai:
Rangkaian Seri
|
Rangkaian Paralel
|
Tegangan (V)
|
Arus (I)
|
Resistansi (R)
|
Konduktansi (G)
|
Reaktansi (X)
|
Susceptansi (B)
|
Impedansi (Z)
|
Admitansi (Y)
|
Kita telah melihat sejauh ini bahwa rangkaian RLC seri dan paralel mengandung reaktansi kapasitif dan reaktansi induktif dalam rangkaian yang sama. Jika kita bervariasi frekuensi di rangkaian ini ada harus menjadi titik dimana nilai reaktansi kapasitif sama bahwa dari reaktansi induktif dan oleh karena itu, XL dan XC. Titik frekuensi di mana hal ini terjadi disebut resonansi dan dalam tutorial berikutnya kita akan melihat Resonansi Seri dan bagaimana kehadirannya mengubah karakteristik rangkaian.