Rangkaian RLC Seri
Rangkaian RLC seri terdiri dari resistansi, kapasitansi, dan induktansi yang dihubungkan secara seri pada supply bolak-balik Sejauh ini kita telah melihat bahwa tiga komponen dasar pasif: Resistor, Induktor, dan Kapasitor memiliki hubungan fasa yang sangat berbeda satu sama lain ketika terhubung ke supply AC (bolak-balik) sinusoidal.
Dalam resistor ohm murni bentuk gelombang tegangan "in-phase" dengan arus. Dalam induktansi murni bentuk gelombang tegangan “memimpin” arus sebesar 90°, memberikan kita ekspresi: ELI. Dalam kapasitansi murni bentuk gelombang tegangan “tertinggal” arus sebesar 90°, memberikan kita ekspresi: ICE.
Perbedaan Fasa ini, Φ tergantung pada nilai reaktif dari komponen yang digunakan dan mudah-mudahan sekarang kita tahu bahwa reaktansi, ( X ) adalah nol jika elemen rangkaian resistif, positif jika elemen rangkaian induktif dan negatif jika kapasitif dengan demikian memberikan impedansi yang dihasilkan sebagai:
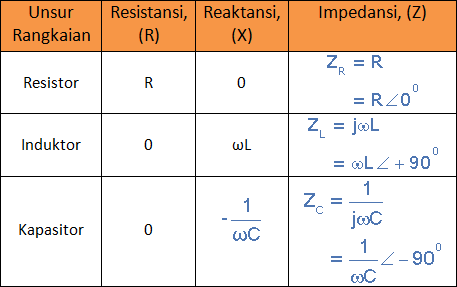
Alih-alih menganalisis setiap elemen pasif secara terpisah, kita dapat menggabungkan ketiganya menjadi rangkaian RLC seri.
Analisis dari RLC seri adalah sama dengan yang untuk ganda seri RL dan RC rangkaian kita melihat sebelumnya, kecuali kali ini kita perlu memperhitungkan besaran dari kedua XL dan XC untuk menemukan rangkaian keseluruhan reaktansi.
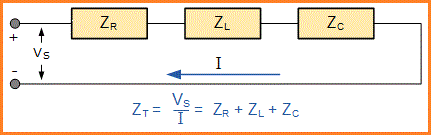
Rangkaian RLC seri digolongkan sebagai rangkaian orde-2 karena mengandung dua unsur penyimpanan energi, induktor L dan kapasitor C. Pertimbangkan rangkaian RLC di bawah ini.
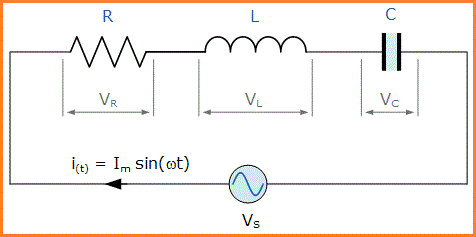
Rangkaian RLC seri di atas memiliki satu loop dengan arus sesaat yang mengalir melalui loop yang sama untuk setiap elemen sirkuit.
Karena reaktansi induktif dan kapasitif XL dan XC adalah fungsi dari frekuensi supply, maka respons sinusoidal dari rangkaian RLC seri akan bervariasi dengan frekuensi, ƒ. Kemudian masing-masing tegangan turun di setiap elemen rangkaian elemen R, L dan C akan "keluar fase" satu sama lain seperti yang didefinisikan berikut:
i(t) = Imaks (ωt)
Tegangan sesaat melintasi resistor murni, VR adalah “dalam-fase” dengan arus
Tegangan sesaat melintasi induktor murni, VL “memimpin” arus sebesar 90°
Tegangan sesaat di kapasitor murni, VC “tertinggal” arus sebesar 90°
Oleh karena itu, VL dan VC 180° “diluar-fasa” dan bertentangan satu sama lain.
Untuk rangkaian RLC seri di atas, ini dapat ditunjukkan sebagai:
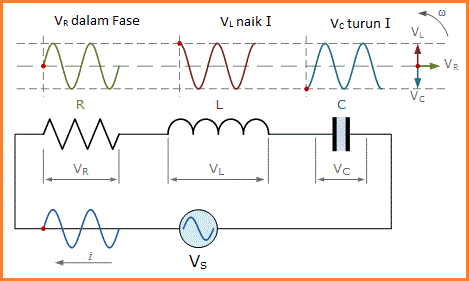
Amplitudo tegangan sumber di ketiga komponen dalam rangkaian RLC seri terdiri dari tiga tegangan komponen individu, VR, VL dan VC dengan arus yang sama untuk ketiga komponen. Diagram vektor karena itu akan memiliki vektor arus sebagai referensi mereka dengan tiga vektor tegangan yang diplot sehubungan dengan referensi ini seperti yang ditunjukkan di bawah ini.
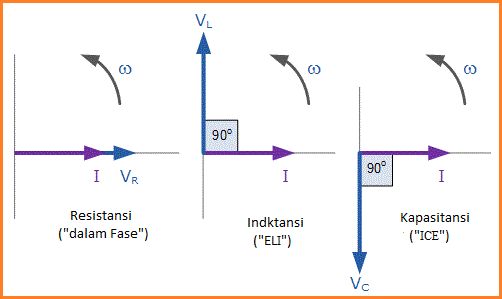
Ini berarti kemudian bahwa kita tidak bisa hanya menambahkan bersama-sama VR, VL dan VC untuk menemukan tegangan supply, VS di semua tiga komponen karena semua tiga vektor tegangan menunjuk dalam arah yang berbeda berkaitan dengan vektor arus. Oleh karena itu kita harus menemukan tegangan supply, VS sebagai jumlah fasor (Fasor Sum) dari tiga tegangan komponen digabungkan bersama-sama secara vektor.
Hukum Kirchoff 2 - Tegangan (KVL) untuk rangkaian loop dan nodal menyatakan bahwa di sekitar loop tertutup, jumlah tegangan turun di sekitar loop sama dengan jumlah GGL. Kemudian menerapkan hukum ini untuk tiga tegangan ini akan memberi kita amplitudo tegangan sumber, VS sebagai.
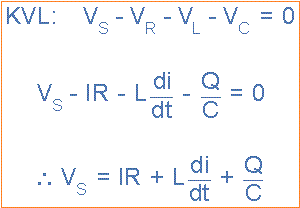
Diagram fasor untuk rangkaian RLC seri dihasilkan dengan menggabungkan bersama-sama tiga fasor individual di atas dan menambahkan tegangan ini secara vektor. Karena arus yang mengalir melalui rangkaian adalah umum untuk ketiga elemen rangkaian, kita dapat menggunakan ini sebagai vektor referensi dengan tiga vektor tegangan yang ditarik relatif terhadap ini pada sudut yang sesuai.
Yang dihasilkan vektor VS diperoleh dengan menambahkan bersama-sama dua vektor, VL dan V C dan kemudian menambahkan jumlah ini ke sisa vektor VR. Sudut yang dihasilkan diperoleh antara VS dan i akan menjadi sudut fase rangkaian seperti yang ditunjukkan di bawah ini.
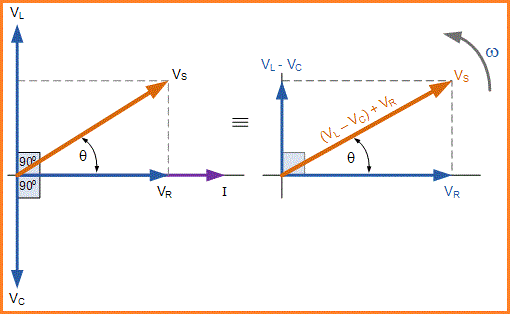
Kita dapat melihat dari diagram fasor di sisi kanan atas bahwa vektor tegangan menghasilkan segitiga persegi panjang, terdiri dari sisi miring VS, sumbu horizontal VR dan sumbu vertikal VL - VC.
Semoga Anda akan memahami kemudian, bahwa ini membentuk favorit lama kami Segitiga Tegangan dan karena itu kita dapat menggunakan teorema Pythagoras pada segitiga tegangan ini untuk secara matematis mendapatkan nilai VS seperti yang ditunjukkan.

Perlu diketahui bahwa bila menggunakan persamaan di atas, tegangan reaktif akhir harus selalu positif dalam nilai, yaitu tegangan terkecil harus selalu diambil dari tegangan terbesar kita tidak bisa memiliki tegangan negatif ditambahkan ke VR sehingga sangat tepat untuk memiliki VL -VC atau VC - VL. Nilai terkecil dari terbesar jika tidak, perhitungan VS akan salah.
Kita tahu dari atas bahwa arus memiliki amplitudo dan fasa yang sama di semua komponen rangkaian RLC seri. Kemudian tegangan di masing-masing komponen juga dapat dijelaskan secara matematis sesuai dengan arus yang mengalir, dan tegangan pada masing-masing elemen.
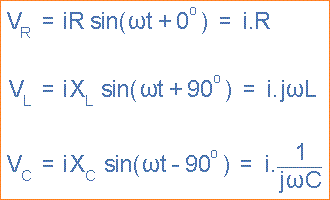
Dengan mengganti nilai-nilai ini ke dalam persamaan Pythagoras di atas untuk segitiga tegangan akan memberi kita:
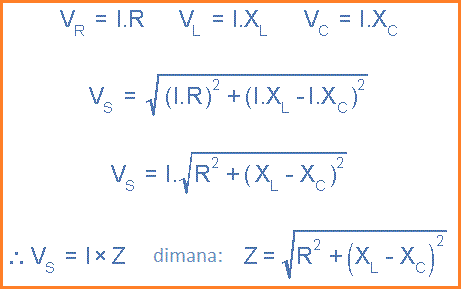
Jadi kita dapat melihat bahwa amplitudo tegangan sumber sebanding dengan amplitudo arus yang mengalir melalui rangkaian. Konstanta proporsionalitas ini disebut Impedansi rangkaian yang pada akhirnya tergantung pada resistansi dan reaktansi kapasitif dan induktif.
Kemudian dalam rangkaian RLC seri di atas, dapat dilihat bahwa perlawanan terhadap aliran arus terdiri dari tiga komponen, XL, XC dan R dengan reaktansi, XT dari rangkaian RLC seri apa pun yang didefinisikan sebagai: XT = XL - XC atau XT = XC - XL mana yang lebih besar. Jadi total impedansi dari rangkaian dianggap sebagai sumber tegangan yang diperlukan untuk menggerakkan arus melaluinya.
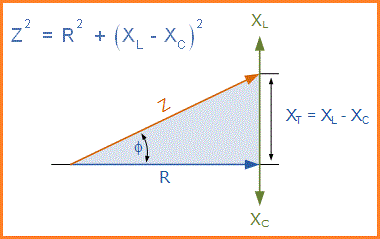
Impedansi Z dari rangkaian RLC seri tergantung pada frekuensi sudut, ω seperti halnya XL dan XC. Jika reaktansi kapasitif lebih besar dari reaktansi induktif, XC > XL maka reaktansi rangkaian keseluruhan kapasitif memberikan sudut fasa terkemuka. Demikian juga, jika reaktansi induktif lebih besar dari reaktansi kapasitif, XL > XC maka keseluruhan reaktansi rangkaian induktif memberikan rangkaian seri sudut fasa tertinggal.
Jika kedua reaktansinya sama dan XL = XC maka frekuensi sudut di mana ini terjadi disebut frekuensi resonansi dan menghasilkan efek resonansi yang akan kita lihat secara lebih rinci dalam tutorial lain waktu. Maka besarnya arus tergantung pada frekuensi yang diterapkan pada rangkaian RLC seri.
Ketika impedansi, Z adalah pada batas maksimum, arus adalah minimum dan demikian pula, ketika Z pada batas minimum, arus pada maksimum. Jadi persamaan di atas untuk impedansi dapat ditulis ulang sebagai:
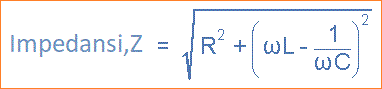
Sudut fasa, θ antara tegangan sumber, VS dan arus, i adalah sama dengan untuk sudut antara Z dan R dalam segitiga impedansi. Sudut fasa ini dapat bernilai positif atau negatif tergantung pada apakah tegangan sumber mengarah atau ketinggalan arus rangkaian dan dapat dihitung secara matematis dari nilai ohmik segitiga impedansi sebagai:
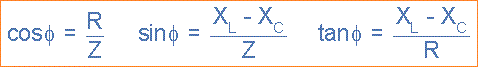
Reaktansi Induktif, XL.
XL = 2πfL = 2πx50x0.15 = 47.13Ω
Reaktansi Kapasitif, XC .
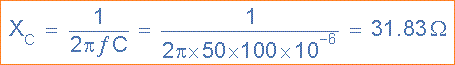
Rangkaian Impedansi, Z .
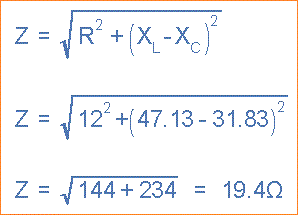
Rangkaian Arus, I.
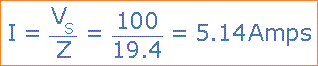
Tegangan melintasi Rangkaian RLC Seri, VR, VL, VC.
VR = I x R = 5.14 x 12 = 61.7 volt
VL = I x XL = 5.14 x 47.13 = 242.2 volt
VC = I x XC = 5.14 x 31.8 =163.5 volt
Rangkaian Faktor daya dan Fase Sudut, θ .
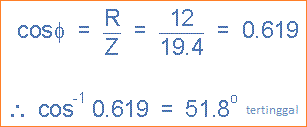
Diagram Fasor
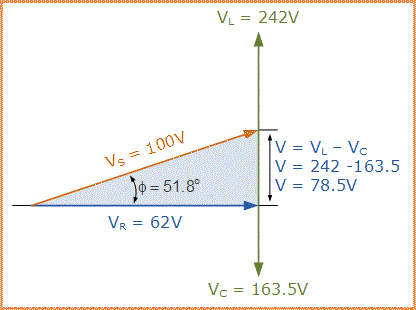
Karena sudut fasa θ dihitung sebagai nilai positif 51,8° keseluruhan reaktansi dari rangkaian harus induktif. Karena kita telah mengambil vektor arus sebagai vektor referensi kita dalam rangkaian RLC seri, maka arus “tertinggal” tegangan sumber sebesar 51,8° sehingga kita dapat mengatakan bahwa sudut fasa tertinggal sebagaimana dikonfirmasi oleh ekspresi mnemonik “ELI”.
Impedansi rangkaian adalah perlawanan total terhadap aliran arus. Untuk RLC seri, dan impedansi segitiga dapat ditarik dengan membagi setiap sisi segitiga tegangan dengan arus, I. Tegangan turun elemen resistif sama dengan I*R, tegangan di dua elemen reaktif adalah I*X = I*XL- I*XC sedangkan sumber tegangan sama dengan I*Z. Sudut antara VS dan I akan menjadi sudut fasa, θ.
Ketika bekerja dengan rangkaian RLC seri yang mengandung banyak resistansi, kapasitansi atau induktansi baik murni atau tidak murni, semuanya dapat ditambahkan bersama untuk membentuk satu komponen tunggal.
Misalnya semua resistansi ditambahkan bersama-sama, RT = (R1 + R2 + R3 )...dst. atau semua induktansi LT = (L1 + L2 + L3 )...dst. dengan cara ini rangkaian yang berisi banyak elemen dapat dengan mudah direduksi menjadi impedansi tunggal.
Dalam tutorial berikutnya tentang Rangkaian RLC Paralel, kita akan melihat hubungan tegangan-arus dari tiga komponen yang terhubung bersama kali ini dalam konfigurasi rangkaian paralel ketika bentuk gelombang AC sinusoidal kondisi mapan diterapkan bersama dengan representasi diagram fasor yang sesuai. Kami juga akan memperkenalkan konsep Penerimaan (Admitansi) untuk pertama kalinya.
Dalam resistor ohm murni bentuk gelombang tegangan "in-phase" dengan arus. Dalam induktansi murni bentuk gelombang tegangan “memimpin” arus sebesar 90°, memberikan kita ekspresi: ELI. Dalam kapasitansi murni bentuk gelombang tegangan “tertinggal” arus sebesar 90°, memberikan kita ekspresi: ICE.
Perbedaan Fasa ini, Φ tergantung pada nilai reaktif dari komponen yang digunakan dan mudah-mudahan sekarang kita tahu bahwa reaktansi, ( X ) adalah nol jika elemen rangkaian resistif, positif jika elemen rangkaian induktif dan negatif jika kapasitif dengan demikian memberikan impedansi yang dihasilkan sebagai:
Unsur/Elemen Impedansi

Alih-alih menganalisis setiap elemen pasif secara terpisah, kita dapat menggabungkan ketiganya menjadi rangkaian RLC seri.
Analisis dari RLC seri adalah sama dengan yang untuk ganda seri RL dan RC rangkaian kita melihat sebelumnya, kecuali kali ini kita perlu memperhitungkan besaran dari kedua XL dan XC untuk menemukan rangkaian keseluruhan reaktansi.
Rangkaian RLC seri digolongkan sebagai rangkaian orde-2 karena mengandung dua unsur penyimpanan energi, induktor L dan kapasitor C. Pertimbangkan rangkaian RLC di bawah ini.
Rangkaian RLC Seri

Rangkaian RLC seri di atas memiliki satu loop dengan arus sesaat yang mengalir melalui loop yang sama untuk setiap elemen sirkuit.
Karena reaktansi induktif dan kapasitif XL dan XC adalah fungsi dari frekuensi supply, maka respons sinusoidal dari rangkaian RLC seri akan bervariasi dengan frekuensi, ƒ. Kemudian masing-masing tegangan turun di setiap elemen rangkaian elemen R, L dan C akan "keluar fase" satu sama lain seperti yang didefinisikan berikut:
i(t) = Imaks (ωt)
Tegangan sesaat melintasi resistor murni, VR adalah “dalam-fase” dengan arus
Tegangan sesaat melintasi induktor murni, VL “memimpin” arus sebesar 90°
Tegangan sesaat di kapasitor murni, VC “tertinggal” arus sebesar 90°
Oleh karena itu, VL dan VC 180° “diluar-fasa” dan bertentangan satu sama lain.
Untuk rangkaian RLC seri di atas, ini dapat ditunjukkan sebagai:

Amplitudo tegangan sumber di ketiga komponen dalam rangkaian RLC seri terdiri dari tiga tegangan komponen individu, VR, VL dan VC dengan arus yang sama untuk ketiga komponen. Diagram vektor karena itu akan memiliki vektor arus sebagai referensi mereka dengan tiga vektor tegangan yang diplot sehubungan dengan referensi ini seperti yang ditunjukkan di bawah ini.
Vektor Tegangan Individu

Ini berarti kemudian bahwa kita tidak bisa hanya menambahkan bersama-sama VR, VL dan VC untuk menemukan tegangan supply, VS di semua tiga komponen karena semua tiga vektor tegangan menunjuk dalam arah yang berbeda berkaitan dengan vektor arus. Oleh karena itu kita harus menemukan tegangan supply, VS sebagai jumlah fasor (Fasor Sum) dari tiga tegangan komponen digabungkan bersama-sama secara vektor.
Hukum Kirchoff 2 - Tegangan (KVL) untuk rangkaian loop dan nodal menyatakan bahwa di sekitar loop tertutup, jumlah tegangan turun di sekitar loop sama dengan jumlah GGL. Kemudian menerapkan hukum ini untuk tiga tegangan ini akan memberi kita amplitudo tegangan sumber, VS sebagai.
Tegangan Seketika/Sesaat untuk Rangkaian RLC Seri
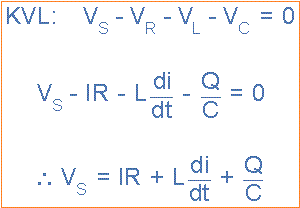
Diagram fasor untuk rangkaian RLC seri dihasilkan dengan menggabungkan bersama-sama tiga fasor individual di atas dan menambahkan tegangan ini secara vektor. Karena arus yang mengalir melalui rangkaian adalah umum untuk ketiga elemen rangkaian, kita dapat menggunakan ini sebagai vektor referensi dengan tiga vektor tegangan yang ditarik relatif terhadap ini pada sudut yang sesuai.
Yang dihasilkan vektor VS diperoleh dengan menambahkan bersama-sama dua vektor, VL dan V C dan kemudian menambahkan jumlah ini ke sisa vektor VR. Sudut yang dihasilkan diperoleh antara VS dan i akan menjadi sudut fase rangkaian seperti yang ditunjukkan di bawah ini.
Diagram Fasor untuk Rangkaian RLC Seri

Kita dapat melihat dari diagram fasor di sisi kanan atas bahwa vektor tegangan menghasilkan segitiga persegi panjang, terdiri dari sisi miring VS, sumbu horizontal VR dan sumbu vertikal VL - VC.
Semoga Anda akan memahami kemudian, bahwa ini membentuk favorit lama kami Segitiga Tegangan dan karena itu kita dapat menggunakan teorema Pythagoras pada segitiga tegangan ini untuk secara matematis mendapatkan nilai VS seperti yang ditunjukkan.
Segitiga Tegangan untuk Rangkaian RLC Seri

Perlu diketahui bahwa bila menggunakan persamaan di atas, tegangan reaktif akhir harus selalu positif dalam nilai, yaitu tegangan terkecil harus selalu diambil dari tegangan terbesar kita tidak bisa memiliki tegangan negatif ditambahkan ke VR sehingga sangat tepat untuk memiliki VL -VC atau VC - VL. Nilai terkecil dari terbesar jika tidak, perhitungan VS akan salah.
Kita tahu dari atas bahwa arus memiliki amplitudo dan fasa yang sama di semua komponen rangkaian RLC seri. Kemudian tegangan di masing-masing komponen juga dapat dijelaskan secara matematis sesuai dengan arus yang mengalir, dan tegangan pada masing-masing elemen.
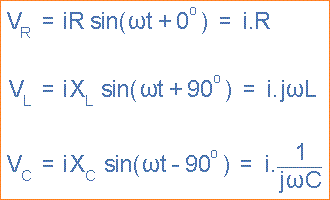
Dengan mengganti nilai-nilai ini ke dalam persamaan Pythagoras di atas untuk segitiga tegangan akan memberi kita:
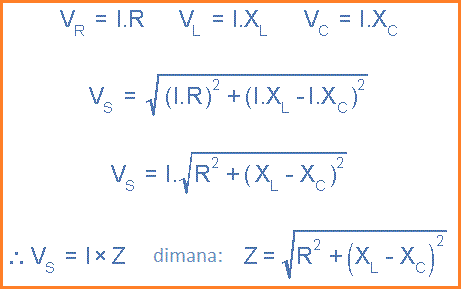
Jadi kita dapat melihat bahwa amplitudo tegangan sumber sebanding dengan amplitudo arus yang mengalir melalui rangkaian. Konstanta proporsionalitas ini disebut Impedansi rangkaian yang pada akhirnya tergantung pada resistansi dan reaktansi kapasitif dan induktif.
Kemudian dalam rangkaian RLC seri di atas, dapat dilihat bahwa perlawanan terhadap aliran arus terdiri dari tiga komponen, XL, XC dan R dengan reaktansi, XT dari rangkaian RLC seri apa pun yang didefinisikan sebagai: XT = XL - XC atau XT = XC - XL mana yang lebih besar. Jadi total impedansi dari rangkaian dianggap sebagai sumber tegangan yang diperlukan untuk menggerakkan arus melaluinya.
Impedansi Rangkaian RLC Seri
Karena ketiga tegangan vektor berada di luar fasa satu sama lain, XL, XC dan R juga harus “out-of-phase” satu sama lain dengan hubungan antara R , XL dan XC sebagai jumlah vektor dari tiga komponen ini. Ini akan memberi kita rangkaian RLC impedansi keseluruhan, Z. Impedansi rangkaian ini dapat ditarik dan diwakili oleh Segitiga Impedansi seperti yang ditunjukkan di bawah ini.Segitiga Impedansi untuk Rangkaian RLC Seri

Impedansi Z dari rangkaian RLC seri tergantung pada frekuensi sudut, ω seperti halnya XL dan XC. Jika reaktansi kapasitif lebih besar dari reaktansi induktif, XC > XL maka reaktansi rangkaian keseluruhan kapasitif memberikan sudut fasa terkemuka. Demikian juga, jika reaktansi induktif lebih besar dari reaktansi kapasitif, XL > XC maka keseluruhan reaktansi rangkaian induktif memberikan rangkaian seri sudut fasa tertinggal.
Jika kedua reaktansinya sama dan XL = XC maka frekuensi sudut di mana ini terjadi disebut frekuensi resonansi dan menghasilkan efek resonansi yang akan kita lihat secara lebih rinci dalam tutorial lain waktu. Maka besarnya arus tergantung pada frekuensi yang diterapkan pada rangkaian RLC seri.
Ketika impedansi, Z adalah pada batas maksimum, arus adalah minimum dan demikian pula, ketika Z pada batas minimum, arus pada maksimum. Jadi persamaan di atas untuk impedansi dapat ditulis ulang sebagai:
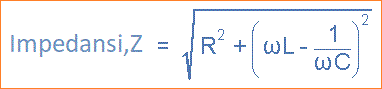
Sudut fasa, θ antara tegangan sumber, VS dan arus, i adalah sama dengan untuk sudut antara Z dan R dalam segitiga impedansi. Sudut fasa ini dapat bernilai positif atau negatif tergantung pada apakah tegangan sumber mengarah atau ketinggalan arus rangkaian dan dapat dihitung secara matematis dari nilai ohmik segitiga impedansi sebagai:
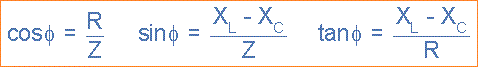
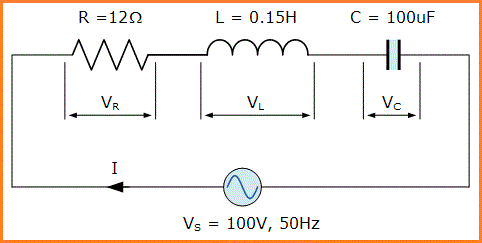
Contoh: Rangkaian RLC Seri No.1
Rangkaian RLC seri yang mengandung resistansi 12Ω, induktansi 0,15H dan kapasitor 100uF dihubungkan secara seri pada supply 100V, 50Hz. Hitung impedansi total rangkaian, arus rangkaian, faktor daya, dan gambar diagram fasor tegangan.
Reaktansi Induktif, XL.
XL = 2πfL = 2πx50x0.15 = 47.13Ω
Reaktansi Kapasitif, XC .
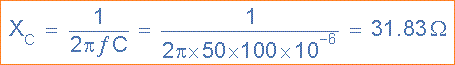
Rangkaian Impedansi, Z .
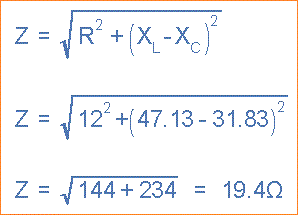
Rangkaian Arus, I.
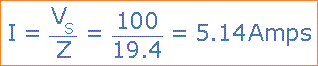
Tegangan melintasi Rangkaian RLC Seri, VR, VL, VC.
VR = I x R = 5.14 x 12 = 61.7 volt
VL = I x XL = 5.14 x 47.13 = 242.2 volt
VC = I x XC = 5.14 x 31.8 =163.5 volt
Rangkaian Faktor daya dan Fase Sudut, θ .
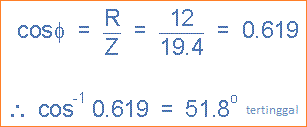
Diagram Fasor

Karena sudut fasa θ dihitung sebagai nilai positif 51,8° keseluruhan reaktansi dari rangkaian harus induktif. Karena kita telah mengambil vektor arus sebagai vektor referensi kita dalam rangkaian RLC seri, maka arus “tertinggal” tegangan sumber sebesar 51,8° sehingga kita dapat mengatakan bahwa sudut fasa tertinggal sebagaimana dikonfirmasi oleh ekspresi mnemonik “ELI”.
Ringkasan Rangkaian RLC Seri
Dalam rangkaian RLC seri yang mengandung resistor, induktor dan kapasitor, sumber tegangan VS adalah jumlah fasor yang terdiri dari tiga komponen, VR, VL dan VC dengan arus yang sama untuk ketiganya. Karena arus umum untuk ketiga komponen itu digunakan sebagai referensi horisontal ketika membangun segitiga tegangan.Impedansi rangkaian adalah perlawanan total terhadap aliran arus. Untuk RLC seri, dan impedansi segitiga dapat ditarik dengan membagi setiap sisi segitiga tegangan dengan arus, I. Tegangan turun elemen resistif sama dengan I*R, tegangan di dua elemen reaktif adalah I*X = I*XL- I*XC sedangkan sumber tegangan sama dengan I*Z. Sudut antara VS dan I akan menjadi sudut fasa, θ.
Ketika bekerja dengan rangkaian RLC seri yang mengandung banyak resistansi, kapasitansi atau induktansi baik murni atau tidak murni, semuanya dapat ditambahkan bersama untuk membentuk satu komponen tunggal.
Misalnya semua resistansi ditambahkan bersama-sama, RT = (R1 + R2 + R3 )...dst. atau semua induktansi LT = (L1 + L2 + L3 )...dst. dengan cara ini rangkaian yang berisi banyak elemen dapat dengan mudah direduksi menjadi impedansi tunggal.

Dalam tutorial berikutnya tentang Rangkaian RLC Paralel, kita akan melihat hubungan tegangan-arus dari tiga komponen yang terhubung bersama kali ini dalam konfigurasi rangkaian paralel ketika bentuk gelombang AC sinusoidal kondisi mapan diterapkan bersama dengan representasi diagram fasor yang sesuai. Kami juga akan memperkenalkan konsep Penerimaan (Admitansi) untuk pertama kalinya.