Hukum Kirchoff 1 - Arus (KCL)
Hukum Kirchoff 1 - Arus (KCL) adalah Hukum pertama Kirchoff yang berkaitan dengan konservasi muatan masuk dan keluar persimpangan/junction.
Untuk menentukan jumlah atau besarnya arus listrik yang mengalir di sekitar rangkaian listrik atau elektronik, kita perlu menggunakan Hukum atau aturan tertentu yang memungkinkan kita untuk menuliskan arus ini dalam bentuk persamaan.
Persamaan jaringan yang digunakan adalah yang menurut Hukum Kirchoff, dan saat kita berhadapan dengan arus rangkaian, kita akan melihat Hukum Kirchoff 1 - Arus, (KCL).
Hukum Kirchoff Arus Gustav adalah salah satu hukum dasar yang digunakan untuk analisis rangkaian. hukumnya Arus menyatakan bahwa untuk jalur paralel, arus total yang memasuki persimpangan rangkaian persis sama dengan arus total yang meninggalkan persimpangan yang sama. Ini karena tidak ada tempat lain untuk pergi karena tidak ada muatan yang hilang.
Dengan kata lain jumlah aljabar SEMUA arus yang masuk dan keluar persimpangan harus sama dengan nol sebagai: Σ IIN = Σ IOUT.
Gagasan oleh Kirchoff ini umumnya dikenal sebagai Konservasi Muatan, karena arus dilestarikan di sekitar persimpangan tanpa kehilangan arus. Mari kita lihat contoh sederhana Hukum Kirchoff 1 - Arus (KCL) ketika diterapkan pada persimpangan tunggal.
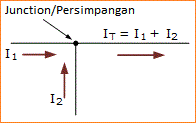
Di sini, dalam contoh persimpangan tunggal sederhana ini, Arus IT meninggalkan persimpangan adalah jumlah aljabar dari dua arus, I1 dan I2 memasuki persimpangan yang sama. Itu adalah IT = I1 + I2. Perhatikan bahwa kita juga bisa menulis ini dengan benar sebagai jumlah aljabar: IT - (I1 + I2) = 0.
Jadi jika I1 sama dengan 3 ampere dan I2 sama dengan 2 ampere, maka total arus, IT yang meninggalkan persimpangan akan menjadi 3 + 2 = 5 ampere, dan kita dapat menggunakan hukum dasar ini untuk sejumlah persimpangan atau simpul seperti jumlah arus yang masuk dan keluar akan sama.
Juga, jika kita membalikkan arah arus, persamaan yang dihasilkan masih berlaku untuk I1 atau I2. Karena I1 = IT - I2 = 5 - 2 = 3 amp, dan I2 = IT - I1 = 5 - 3 = 2 amp. Dengan demikian kita dapat menganggap arus yang memasuki persimpangan sebagai positif (+), sedangkan yang meninggalkan persimpangan sebagai negatif (-).
Kemudian kita dapat melihat bahwa jumlah matematis dari arus yang masuk atau meninggalkan persimpangan dan ke arah mana pun akan selalu sama dengan nol, dan ini membentuk dasar Peraturan Persimpangan Kirchoff, lebih dikenal sebagai Hukum Kirchoff 1 - Arus, atau (KCL).
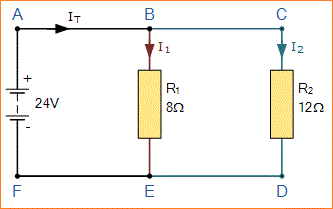
Dalam contoh resistor paralel sederhana ini ada dua persimpangan yang berbeda untuk arus. Persimpangan satu terjadi pada simpul B, dan persimpangan dua terjadi pada simpul E.
Dengan demikian kita dapat menggunakan Hukum Persimpangan Kirchoff untuk arus listrik pada kedua persimpangan yang berbeda ini, untuk arus yang memasuki persimpangan dan untuk arus yang mengalir meninggalkan persimpangan.
Untuk memulai, arus total, IT meninggalkan supply 24 volt dan tiba di titik A dan dari sana memasuki simpul B. Node B adalah persimpangan karena arus kini dapat dibagi menjadi dua arah yang berbeda, dengan beberapa arus mengalir ke bawah dan melalui resistor R1 dengan sisanya melanjutkan melalui resistor R2 melalui simpul C. Perhatikan bahwa arus yang mengalir masuk dan keluar dari titik simpul biasanya disebut arus cabang.
Kita dapat menggunakan Hukum Ohm untuk menentukan arus cabang individu melalui masing-masing Resistor sebagai: I = V/R, dengan demikian:
Untuk cabang Arus B ke E melalui resistor R1
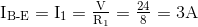
Untuk cabang Arus C ke D melalui resistor R2
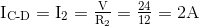
Dari atas kita tahu bahwa Hukum Kirchoff 1 - Arus menyatakan bahwa jumlah arus yang memasuki persimpangan harus sama dengan jumlah arus yang meninggalkan persimpangan, dan dalam contoh sederhana kami di atas, ada satu arus, IT pergi ke persimpangan di simpul B dan dua arus meninggalkan persimpangan, I1 dan I2.
Karena kita sekarang tahu dari perhitungan bahwa arus yang meninggalkan persimpangan pada simpul B adalah I1 sama dengan 3 amp dan I2 sama dengan 2 amp, jumlah arus yang memasuki persimpangan pada simpul B harus sama dengan 3 + 2 = 5 amp. Jadi ΣIN = IT = 5 ampere.
Dalam contoh kami, kami memiliki dua persimpangan berbeda pada simpul B dan simpul E, sehingga kami dapat mengonfirmasi nilai ini untuk IT ketika dua arus bergabung kembali di simpul E.
Jadi, agar aturan persimpangan Kirchoff tetap benar, jumlah arus ke titik F harus sama dengan jumlah arus yang mengalir keluar dari persimpangan di simpul E.
Karena dua arus yang memasuki persimpangan E adalah masing-masing 3 amp dan 2 amp, maka jumlah arus yang memasuki titik F adalah: 3 + 2 = 5 ampere. Jadi ΣIN = IT = 5 ampere dan karena itu Hukum Kirchoff 1 - Arus berlaku karena ini adalah nilai yang sama dengan titik berangkat Arus A.
Mudah-mudahan kita tahu sekarang bahwa jumlah aljabar semua arus pada sebuah simpul (titik persimpangan) sama dengan nol dan dengan pemikiran ini.
Ini adalah kasus sederhana untuk menentukan arus yang memasuki sebuah simpul dan yang meninggalkan simpul. Pertimbangkan rangkaian di bawah ini.
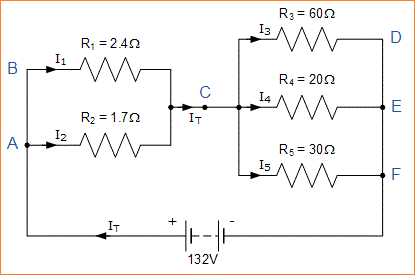
Dalam contoh ini ada empat persimpangan berbeda untuk arus untuk memisahkan atau menggabungkan bersama pada simpul A, C, E dan simpul F. Arus supply IT memisahkan pada simpul A yang mengalir melalui resistor R1 dan R2, menggabungkan kembali pada simpul C sebelum memisahkan lagi melalui resistor R3, R4 dan R5 dan akhirnya menggabungkan kembali sekali lagi pada simpul F.
Tapi sebelum kita dapat menghitung arus individu yang mengalir melalui setiap cabang resistor, pertama kita harus menghitung Total rangkaian Arus, IT. Hukum Ohm memberi tahu kita bahwa I = V/R dan seperti yang kita ketahui nilai V, 132 volt, kita perlu menghitung resistansi rangkaian sebagai berikut.
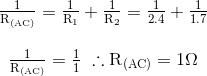
Dengan demikian resistansi rangkaian ekuivalen antara node A dan C dihitung sebagai 1 Ohm.
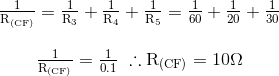
Dengan demikian resistansi rangkaian ekuivalen antara node C dan F dihitung sebagai 10 Ohm. Kemudian total arus rangkaian, IT diberikan sebagai:
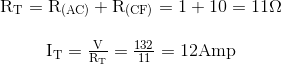
Memberi kita rangkaian ekuivalen/setara:
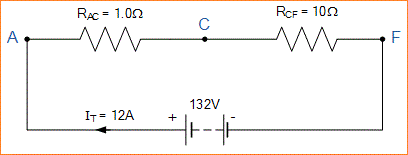
Oleh karena itu, V = 132V, RAC = 1Ω, RCF = 10Ω dan IT = 12A.
Setelah menetapkan resistansi paralel yang setara dan arus supply/pasokan, kita sekarang dapat menghitung arus cabang individu dan mengonfirmasi menggunakan aturan persimpangan Kirchoff sebagai berikut.
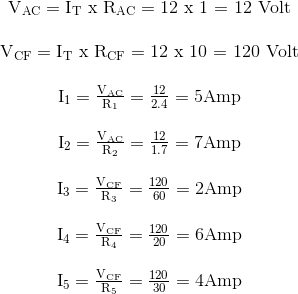
Kami dapat mengonfirmasi bahwa Hukum Kirchoff 1 - Arus berlaku di sekitar rangkaian dengan menggunakan simpul C sebagai titik referensi kami untuk menghitung arus yang masuk dan keluar dari persimpangan sebagai:
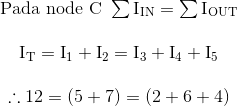
Kita juga dapat memeriksa ulang untuk melihat apakah Hukum Kirchoff 1 - Arus berlaku sebagai arus masuk persimpangan positif, sedangkan yang meninggalkan persimpangan negatif, dengan demikian jumlah aljabar adalah: I1 + I2 - I3 - I4 - I5 = 0 yang sama dengan 5 + 7 - 2 - 6 - 4 = 0.
Jadi kita dapat mengkonfirmasi dengan analisis bahwa Hukum Kirchoff 1 - Arus (KCL) yang menyatakan bahwa jumlah aljabar arus pada titik persimpangan dalam jaringan rangkaian selalu nol adalah benar dan benar dalam contoh ini.
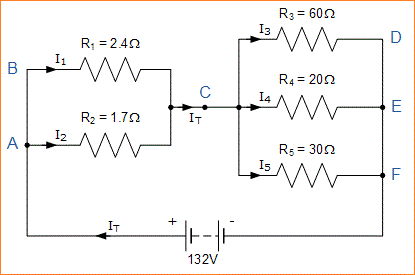
IT adalah total arus yang mengalir di sekitar rangkaian yang digerakkan oleh tegangan supply 12V. Pada titik A, I1 sama dengan IT, dengan demikian akan ada I1*R tegangan drop di resistor R1.
Rangkaian memiliki 2 cabang, 3 node (B, C dan D) dan 2 loop independen, sehingga tegangan I*R turun di sekitar dua loop adalah:
Loop ABC ⇒ 12 = 4I1 + 6I2
Loop ABD ⇒ 12 = 4I1 + 12I3
Karena Hukum Kirchoff 1 - Arus menyatakan bahwa pada simpul B, I1 = I2 + I3, oleh karena itu kita dapat mengganti I1 Arus dengan (I2 + I3) di kedua persamaan loop berikut dan kemudian menyederhanakan.
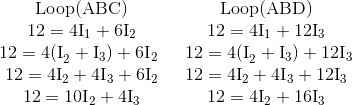
Kita sekarang memiliki dua persamaan simultan yang berhubungan dengan arus yang mengalir di sekitar rangkaian.
Pers. No 1: 12 = 10I2 + 4I3
Pers. No 2: 12 = 4I2 + 16I3
Dengan mengalikan persamaan pertama (Loop ABC) dengan 4 dan mengurangi Loop ABD dari Loop ABC, kita dapat mengurangi kedua persamaan untuk memberi kita nilai I2 dan I3
Pers. No 1: 12 = 10I2 + 4I3 (x4) ⇒ 48 = 40I2 + 16I3
Pers. No 2: 12 = 4I2 + 16I3 (x1) ⇒ 12 = 4I2 + 16I3
Pers. No 1 - Persamaan. No 2 ⇒ 36 = 36I2 + 0
Substitusi I2 dalam hal I3 memberi kita nilai I2 sebagai 1,0 Amps
Sekarang kita dapat melakukan prosedur yang sama untuk menemukan nilai I3 dengan mengalikan persamaan pertama (Loop ABC) dengan 4 dan persamaan kedua (Loop ABD) dengan 10. Sekali lagi dengan mengurangi Loop ABC dari Loop ABD, kita dapat mengurangi keduanya persamaan untuk memberi kita nilai I2 dan I3
Pers. No 1: 12 = 10I2 + 4I3 (x4) ⇒ 48 = 40I2 + 16I3
Pers. No 2: 12 = 4I2 + 16I3 (x10) ⇒ 120 = 40I2 + 160I3
Pers. No 2 - Persamaan. No 1 ⇒ 72 = 0 + 144I3
Jadi substitusi I3 dalam hal I2 memberi kita nilai I3 sebagai 0,5 Amps
Sebagai aturan persimpangan Kirchoff menyatakan bahwa: I1 = I2 + I3
Pasokan arus yang mengalir melalui resistor R1 diberikan sebagai: 1,0 + 0,5 = 1,5 Amps
Jadi I1 = IT = 1.5 Amps, I2 = 1.0 Amps dan I3 = 0.5 Amps dan dari informasi itu kita dapat menghitung penurunan tegangan I*R di seluruh perangkat dan di berbagai titik (node) di sekitar rangkaian.
Kita dapat memecahkan rangkaian contoh dua dengan sederhana dan mudah hanya menggunakan Hukum Ohm, tetapi kami telah menggunakan Hukum Kirchoff 1 - Arus di sini untuk menunjukkan bagaimana mungkin untuk menyelesaikan rangkaian yang lebih kompleks ketika kita tidak bisa begitu saja menerapkan Hukum Ohm.
Untuk menentukan jumlah atau besarnya arus listrik yang mengalir di sekitar rangkaian listrik atau elektronik, kita perlu menggunakan Hukum atau aturan tertentu yang memungkinkan kita untuk menuliskan arus ini dalam bentuk persamaan.
Persamaan jaringan yang digunakan adalah yang menurut Hukum Kirchoff, dan saat kita berhadapan dengan arus rangkaian, kita akan melihat Hukum Kirchoff 1 - Arus, (KCL).
Hukum Kirchoff Arus Gustav adalah salah satu hukum dasar yang digunakan untuk analisis rangkaian. hukumnya Arus menyatakan bahwa untuk jalur paralel, arus total yang memasuki persimpangan rangkaian persis sama dengan arus total yang meninggalkan persimpangan yang sama. Ini karena tidak ada tempat lain untuk pergi karena tidak ada muatan yang hilang.
Dengan kata lain jumlah aljabar SEMUA arus yang masuk dan keluar persimpangan harus sama dengan nol sebagai: Σ IIN = Σ IOUT.
Gagasan oleh Kirchoff ini umumnya dikenal sebagai Konservasi Muatan, karena arus dilestarikan di sekitar persimpangan tanpa kehilangan arus. Mari kita lihat contoh sederhana Hukum Kirchoff 1 - Arus (KCL) ketika diterapkan pada persimpangan tunggal.
Persimpangan Tunggal (single junction)

Jadi jika I1 sama dengan 3 ampere dan I2 sama dengan 2 ampere, maka total arus, IT yang meninggalkan persimpangan akan menjadi 3 + 2 = 5 ampere, dan kita dapat menggunakan hukum dasar ini untuk sejumlah persimpangan atau simpul seperti jumlah arus yang masuk dan keluar akan sama.
Juga, jika kita membalikkan arah arus, persamaan yang dihasilkan masih berlaku untuk I1 atau I2. Karena I1 = IT - I2 = 5 - 2 = 3 amp, dan I2 = IT - I1 = 5 - 3 = 2 amp. Dengan demikian kita dapat menganggap arus yang memasuki persimpangan sebagai positif (+), sedangkan yang meninggalkan persimpangan sebagai negatif (-).
Kemudian kita dapat melihat bahwa jumlah matematis dari arus yang masuk atau meninggalkan persimpangan dan ke arah mana pun akan selalu sama dengan nol, dan ini membentuk dasar Peraturan Persimpangan Kirchoff, lebih dikenal sebagai Hukum Kirchoff 1 - Arus, atau (KCL).
Resistor dalam Paralel
Mari kita lihat bagaimana kita bisa menerapkan Hukum Kirchoff 1 - Arus pada Resistor secara paralel, apakah resistansi hambatan di cabang-cabang itu sama atau tidak sama. Pertimbangkan diagram rangkaian berikut:
Dalam contoh resistor paralel sederhana ini ada dua persimpangan yang berbeda untuk arus. Persimpangan satu terjadi pada simpul B, dan persimpangan dua terjadi pada simpul E.
Dengan demikian kita dapat menggunakan Hukum Persimpangan Kirchoff untuk arus listrik pada kedua persimpangan yang berbeda ini, untuk arus yang memasuki persimpangan dan untuk arus yang mengalir meninggalkan persimpangan.
Untuk memulai, arus total, IT meninggalkan supply 24 volt dan tiba di titik A dan dari sana memasuki simpul B. Node B adalah persimpangan karena arus kini dapat dibagi menjadi dua arah yang berbeda, dengan beberapa arus mengalir ke bawah dan melalui resistor R1 dengan sisanya melanjutkan melalui resistor R2 melalui simpul C. Perhatikan bahwa arus yang mengalir masuk dan keluar dari titik simpul biasanya disebut arus cabang.
Kita dapat menggunakan Hukum Ohm untuk menentukan arus cabang individu melalui masing-masing Resistor sebagai: I = V/R, dengan demikian:
Untuk cabang Arus B ke E melalui resistor R1
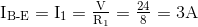
Untuk cabang Arus C ke D melalui resistor R2
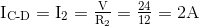
Dari atas kita tahu bahwa Hukum Kirchoff 1 - Arus menyatakan bahwa jumlah arus yang memasuki persimpangan harus sama dengan jumlah arus yang meninggalkan persimpangan, dan dalam contoh sederhana kami di atas, ada satu arus, IT pergi ke persimpangan di simpul B dan dua arus meninggalkan persimpangan, I1 dan I2.
Karena kita sekarang tahu dari perhitungan bahwa arus yang meninggalkan persimpangan pada simpul B adalah I1 sama dengan 3 amp dan I2 sama dengan 2 amp, jumlah arus yang memasuki persimpangan pada simpul B harus sama dengan 3 + 2 = 5 amp. Jadi ΣIN = IT = 5 ampere.
Dalam contoh kami, kami memiliki dua persimpangan berbeda pada simpul B dan simpul E, sehingga kami dapat mengonfirmasi nilai ini untuk IT ketika dua arus bergabung kembali di simpul E.
Jadi, agar aturan persimpangan Kirchoff tetap benar, jumlah arus ke titik F harus sama dengan jumlah arus yang mengalir keluar dari persimpangan di simpul E.
Karena dua arus yang memasuki persimpangan E adalah masing-masing 3 amp dan 2 amp, maka jumlah arus yang memasuki titik F adalah: 3 + 2 = 5 ampere. Jadi ΣIN = IT = 5 ampere dan karena itu Hukum Kirchoff 1 - Arus berlaku karena ini adalah nilai yang sama dengan titik berangkat Arus A.
Menerapkan Hukum Kirchoff 1 - Arus ke Rangkaian yang Lebih Kompleks
Kita dapat menggunakan Hukum Kirchoff 1 - Arus untuk menemukan arus yang mengalir di sekitar rangkaian yang lebih kompleks.Mudah-mudahan kita tahu sekarang bahwa jumlah aljabar semua arus pada sebuah simpul (titik persimpangan) sama dengan nol dan dengan pemikiran ini.
Ini adalah kasus sederhana untuk menentukan arus yang memasuki sebuah simpul dan yang meninggalkan simpul. Pertimbangkan rangkaian di bawah ini.
Contoh Hukum Kirchoff 1 - Arus No.1

Dalam contoh ini ada empat persimpangan berbeda untuk arus untuk memisahkan atau menggabungkan bersama pada simpul A, C, E dan simpul F. Arus supply IT memisahkan pada simpul A yang mengalir melalui resistor R1 dan R2, menggabungkan kembali pada simpul C sebelum memisahkan lagi melalui resistor R3, R4 dan R5 dan akhirnya menggabungkan kembali sekali lagi pada simpul F.
Tapi sebelum kita dapat menghitung arus individu yang mengalir melalui setiap cabang resistor, pertama kita harus menghitung Total rangkaian Arus, IT. Hukum Ohm memberi tahu kita bahwa I = V/R dan seperti yang kita ketahui nilai V, 132 volt, kita perlu menghitung resistansi rangkaian sebagai berikut.
Resistansi Rangkaian RAC
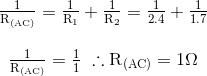
Dengan demikian resistansi rangkaian ekuivalen antara node A dan C dihitung sebagai 1 Ohm.
Resistansi Rangkaian RCF
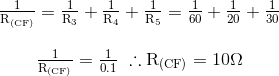
Dengan demikian resistansi rangkaian ekuivalen antara node C dan F dihitung sebagai 10 Ohm. Kemudian total arus rangkaian, IT diberikan sebagai:
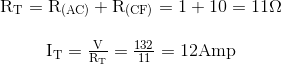
Memberi kita rangkaian ekuivalen/setara:
Rangkaian Ekuivalen/Setara Hukum Kirchoff 1 - Arus

Oleh karena itu, V = 132V, RAC = 1Ω, RCF = 10Ω dan IT = 12A.
Setelah menetapkan resistansi paralel yang setara dan arus supply/pasokan, kita sekarang dapat menghitung arus cabang individu dan mengonfirmasi menggunakan aturan persimpangan Kirchoff sebagai berikut.
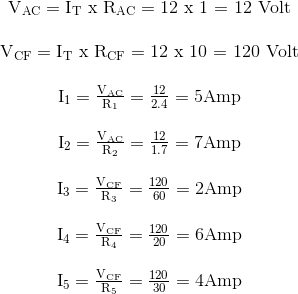
Jadi, I1 = 5A, I2 = 7A, I3 = 2A, I4 = 6A, dan I5 = 4A.
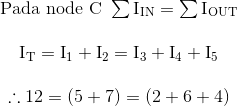
Kita juga dapat memeriksa ulang untuk melihat apakah Hukum Kirchoff 1 - Arus berlaku sebagai arus masuk persimpangan positif, sedangkan yang meninggalkan persimpangan negatif, dengan demikian jumlah aljabar adalah: I1 + I2 - I3 - I4 - I5 = 0 yang sama dengan 5 + 7 - 2 - 6 - 4 = 0.
Jadi kita dapat mengkonfirmasi dengan analisis bahwa Hukum Kirchoff 1 - Arus (KCL) yang menyatakan bahwa jumlah aljabar arus pada titik persimpangan dalam jaringan rangkaian selalu nol adalah benar dan benar dalam contoh ini.
Contoh Hukum Kirchoff 1 - Arus No.2
Temukan arus yang mengalir di sekitar rangkaian berikut hanya dengan menggunakan Hukum Kirchoff 1- Arus.
IT adalah total arus yang mengalir di sekitar rangkaian yang digerakkan oleh tegangan supply 12V. Pada titik A, I1 sama dengan IT, dengan demikian akan ada I1*R tegangan drop di resistor R1.
Rangkaian memiliki 2 cabang, 3 node (B, C dan D) dan 2 loop independen, sehingga tegangan I*R turun di sekitar dua loop adalah:
Loop ABC ⇒ 12 = 4I1 + 6I2
Loop ABD ⇒ 12 = 4I1 + 12I3
Karena Hukum Kirchoff 1 - Arus menyatakan bahwa pada simpul B, I1 = I2 + I3, oleh karena itu kita dapat mengganti I1 Arus dengan (I2 + I3) di kedua persamaan loop berikut dan kemudian menyederhanakan.
Persamaan Loop Kirchoff
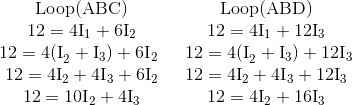
Kita sekarang memiliki dua persamaan simultan yang berhubungan dengan arus yang mengalir di sekitar rangkaian.
Pers. No 1: 12 = 10I2 + 4I3
Pers. No 2: 12 = 4I2 + 16I3
Dengan mengalikan persamaan pertama (Loop ABC) dengan 4 dan mengurangi Loop ABD dari Loop ABC, kita dapat mengurangi kedua persamaan untuk memberi kita nilai I2 dan I3
Pers. No 1: 12 = 10I2 + 4I3 (x4) ⇒ 48 = 40I2 + 16I3
Pers. No 2: 12 = 4I2 + 16I3 (x1) ⇒ 12 = 4I2 + 16I3
Pers. No 1 - Persamaan. No 2 ⇒ 36 = 36I2 + 0
Substitusi I2 dalam hal I3 memberi kita nilai I2 sebagai 1,0 Amps
Sekarang kita dapat melakukan prosedur yang sama untuk menemukan nilai I3 dengan mengalikan persamaan pertama (Loop ABC) dengan 4 dan persamaan kedua (Loop ABD) dengan 10. Sekali lagi dengan mengurangi Loop ABC dari Loop ABD, kita dapat mengurangi keduanya persamaan untuk memberi kita nilai I2 dan I3
Pers. No 1: 12 = 10I2 + 4I3 (x4) ⇒ 48 = 40I2 + 16I3
Pers. No 2: 12 = 4I2 + 16I3 (x10) ⇒ 120 = 40I2 + 160I3
Pers. No 2 - Persamaan. No 1 ⇒ 72 = 0 + 144I3
Jadi substitusi I3 dalam hal I2 memberi kita nilai I3 sebagai 0,5 Amps
Sebagai aturan persimpangan Kirchoff menyatakan bahwa: I1 = I2 + I3
Pasokan arus yang mengalir melalui resistor R1 diberikan sebagai: 1,0 + 0,5 = 1,5 Amps
Jadi I1 = IT = 1.5 Amps, I2 = 1.0 Amps dan I3 = 0.5 Amps dan dari informasi itu kita dapat menghitung penurunan tegangan I*R di seluruh perangkat dan di berbagai titik (node) di sekitar rangkaian.
Kita dapat memecahkan rangkaian contoh dua dengan sederhana dan mudah hanya menggunakan Hukum Ohm, tetapi kami telah menggunakan Hukum Kirchoff 1 - Arus di sini untuk menunjukkan bagaimana mungkin untuk menyelesaikan rangkaian yang lebih kompleks ketika kita tidak bisa begitu saja menerapkan Hukum Ohm.