Penjumlahan Bilangan Biner
Penjumlahan Bilangan Biner adalah rangkaian aritmatika dalam bentuk half-adders dan full-adders yang digunakan untuk menjumlahkan dua digit biner.
Rangkaian logika kombinasional umum dan sangat berguna lainnya yang dapat dibangun menggunakan hanya beberapa gerbang logika dasar yang memungkinkannya untuk menambahkan bersama dua atau lebih angka biner adalah Penjumlahan Bilangan Biner.
Sebuah rangkaian penjumlahan biner dasar dapat dibuat dari standar gerbang AND dan gerbang Ex-OR memungkinkan kita untuk “menambahkan” bersama-sama dua angka biner tunggal bit, A dan B.
Penjumlahan dua digit ini menghasilkan output yang disebut JUMLAH dari penjumlahan dan output kedua disebut bit CARRY atau Carry-out, (COUT) sesuai dengan aturan untuk penjumlahan biner.
Salah satu kegunaan utama untuk Penjumlahan Bilangan Biner adalah dalam rangkaian hitung dan penghitungan. Pertimbangkan penjumlahan sederhana dari dua nomor denary (base 10) di bawah ini.
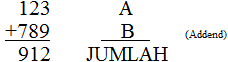
Dari pelajaran matematika kita di sekolah, kita belajar bahwa setiap kolom angka ditambahkan bersama-sama mulai dari sisi kanan dan bahwa setiap digit memiliki nilai tertimbang tergantung pada posisinya di dalam kolom.
Ketika setiap kolom ditambahkan bersama-sama, sebuah carry dihasilkan jika hasilnya lebih besar atau sama dengan 10, angka dasar. Carry ini kemudian ditambahkan ke hasil penjumlahan kolom berikutnya ke kiri dan seterusnya, penjumlahan matematika sekolah sederhana, tambahkan angka dan bawa.
Menambahkan bilangan biner adalah ide yang sama persis dengan penjumlahan bilangan desimal tetapi kali ini carry hanya dihasilkan ketika hasil di kolom mana pun lebih besar atau sama dengan "2", angka dasar dari biner. Dengan kata lain 1 + 1 menciptakan carry.
Jadi ketika menambahkan bilangan biner, suatu hasil dihasilkan ketika "JUMLAH" sama dengan atau lebih besar dari dua (1 +1) dan ini menjadi bit "CARRY" untuk setiap penjumlahan berikutnya yang diteruskan ke kolom berikutnya untuk penjumlahan dan seterusnya di. Pertimbangkan penjumlahan bit tunggal di bawah ini.
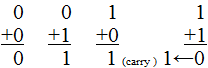
Ketika dua bit tunggal, A dan B ditambahkan bersama-sama, penjumlahan "0 + 0", "0 + 1" dan "1 + 0" menghasilkan "0" atau "1" hingga Anda mencapai Kolom terakhir "1 + 1" maka jumlahnya sama dengan "2". Tetapi nomor dua tidak ada dalam biner, 2 dalam biner sama dengan 10 , dengan kata lain nol untuk jumlah plus sedikit carry bit.
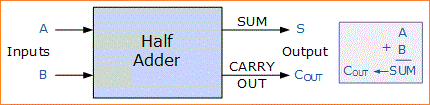
Maka pengoperasian penjumlahan sederhana memerlukan dua input data yang menghasilkan dua output, jumlah (S) dari persamaan dan bit Carry (C) seperti yang ditunjukkan.
Untuk masalah penjumlahan 1-bit sederhana di atas, carry bit yang dihasilkan dapat diabaikan tetapi Anda mungkin telah memperhatikan hal lain sehubungan dengan penjumlahan dua bit ini, jumlah penjumlahan binernya menyerupai Gerbang Exclusive-OR.
Jika kita memberi label dua bit sebagai A dan B maka tabel kebenaran yang dihasilkan adalah jumlah dari dua bit tetapi tanpa carry final.
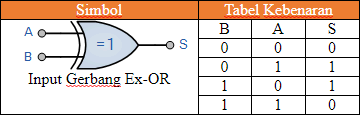
Kita dapat melihat dari tabel kebenaran di atas, bahwa gerbang Exclusive-OR hanya menghasilkan output "1" ketika salah satu input berada pada logika "1", tetapi tidak keduanya sama dengan penjumlahan biner dari dua bit sebelumnya.
Namun untuk melakukan penjumlahan dua angka, mikroprosesor dan kalkulator elektronik memerlukan bit carry tambahan untuk menghitung persamaan dengan benar sehingga kita perlu menulis ulang penjumlahan sebelumnya untuk memasukkan dua-bit data output seperti yang ditunjukkan di bawah ini.
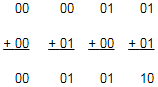
Dari persamaan di atas kita sekarang tahu bahwa gerbang Exclusive-OR hanya akan menghasilkan output "1" ketika input "ANTARA" berada pada logika "1", jadi kita membutuhkan output tambahan untuk menghasilkan bit carry ketika "KEDUA" input A dan B berada pada logika "1".
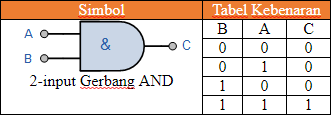
Satu gerbang digital yang pas dengan tagihan menghasilkan output "1" ketika kedua input A dan B adalah "1" (TINGGI) adalah standar Gerbang AND.
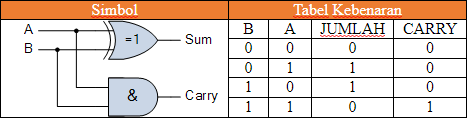
Dengan menggabungkan gerbang Exclusive-OR dengan gerbang AND menghasilkan rangkaian penjumlahan biner digital sederhana yang umumnya dikenal sebagai rangkaian setengah penjumlahan atau "Half Adder".
Dari tabel kebenaran setengah penjumlahan kita dapat melihat bahwa output JUMLAH ( S ) adalah hasil dari gerbang Exclusive-OR dan Carry-out ( Cout ) adalah hasil dari gerbang AND. Maka ekspresi Boolean untuk setengah penjumlahan adalah sebagai berikut.
Untuk bit JUMLAH :
Untuk bit CARRY:
Salah satu kelemahan utama dari rangkaian Half Adder ketika digunakan sebagai penjumlahan biner, adalah bahwa tidak ada ketentuan untuk "Carry-in" dari rangkaian sebelumnya ketika menambahkan bersama beberapa bit data.
Sebagai contoh, misalkan kita ingin menambahkan dua byte data 8-bit, bit carry apa pun yang dihasilkan harus dapat "beriak" atau bergerak melintasi pola bit mulai dari bit paling tidak signifikan (LSB).
Operasi yang paling rumit yang dapat dilakukan setengah penjumlahan adalah "1+1" tetapi karena setengah penjumlahan tidak memiliki input carry, nilai tambah yang dihasilkan akan salah. Salah satu cara sederhana untuk mengatasi masalah ini adalah dengan menggunakan rangkaian penjumlahan tipe biner Full Adder.
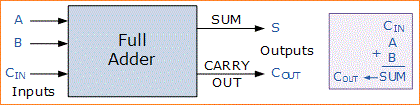
Kemudian penjumlahan penuh adalah rangkaian logika yang melakukan operasi tambahan pada tiga digit biner dan seperti penjumlahan setengah, itu juga menghasilkan melaksanakan ke kolom tambahan berikutnya.
Maka Carry-in adalah carry yang mungkin dari digit yang kurang signifikan, sementara Carry-out mewakili carry ke digit yang lebih signifikan.
Dalam banyak hal, penjumlahan penuh dapat dianggap sebagai dua penjumlahan setengah terhubung bersama-sama, dengan penjumlahan babak pertama meneruskan tugasnya ke penjumlahan babak kedua seperti yang ditunjukkan.
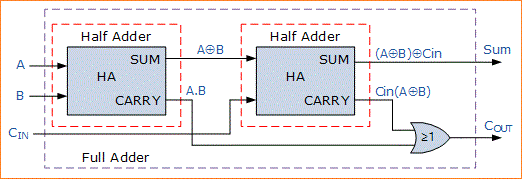
Karena rangkaian penjumlahan penuh di atas pada dasarnya adalah dua setengah pembahan yang terhubung bersama, tabel kebenaran untuk penjumlahan penuh mencakup kolom tambahan untuk memperhitungkan input Carry-in, CIN serta output yang dijumlahkan, S dan Carry-out , COUT bit.
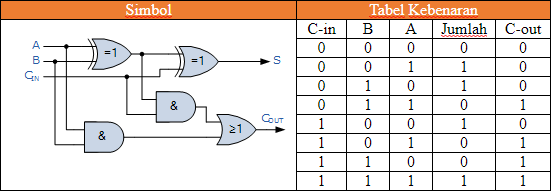
Maka ekspresi Boolean untuk penjumlahan penuh adalah sebagai berikut.
Untuk bit JUMLAH ( S ):
Untuk bit CARRY-OUT ( Cout ):
Ripple Carry Adder sebuah "n", full adder 1-bit yang di-cascade bersama dengan tiap full adder dan kemudian akan mewakili kolom tunggal tertimbang pada adder biner yang panjang.
Ini disebut adder ripple carry karena sinyal carry menghasilkan efek "ripple" melalui penjumlahan biner dari kanan ke kiri, (LSB ke MSB).
Sebagai contoh, misalkan kita ingin "menambahkan" bersama dua angka 4-bit, dua output dari penjumlahan penuh pertama akan memberikan jumlah digit tempat pertama ( S ) dari penjumlahan ditambah bit carry-out yang bertindak sebagai carry dalam digit penjumlahan biner berikutnya.
Penjumlahan biner kedua dalam rantai juga menghasilkan output yang dijumlahkan (bit ke-2) ditambah bit carry-out lainnya dan kita dapat terus menambahkan lebih banyak penjumlahan penuh pada kombinasi untuk menambahkan angka yang lebih besar, menghubungkan output bit carry dari penjumlahan biner penuh pertama ke penjumlahan penuh berikutnya, dan sebagainya.
Contoh dari penjumlahan 4-bit diberikan di bawah ini.
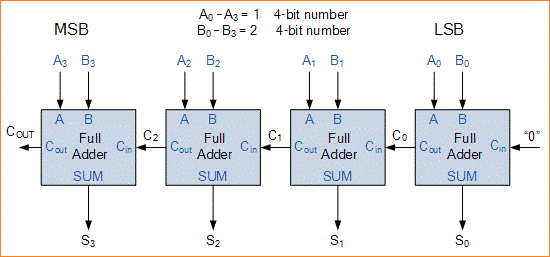
Salah satu kelemahan utama dari “cascading” bersama-sama 1-bit penjumlahan biner untuk menambah angka biner yang besar adalah bahwa jika input A dan B berubah, jumlah pada outputnya tidak akan valid sampai semua carry-input telah “rippled” melalui setiap penjumlahan penuh di rantai karena MSB (bit paling signifikan) dari jumlah harus menunggu perubahan dari input carry LSB (bit kurang signifikan).
Akibatnya, akan ada penundaan yang terbatas sebelum output dari penambah menanggapi setiap perubahan dalam inputnya yang menghasilkan penundaan akumulasi.
Ketika ukuran bit yang ditambahkan tidak terlalu besar misalnya, 4 atau 8 bit, atau kecepatan penjumlahan dari penambah tidak penting, penundaan ini mungkin tidak penting.
Namun, ketika ukuran bit lebih besar misalnya 32 atau 64 bit yang digunakan dalam penjumlahan multi-bit, atau penjumlahan diperlukan pada kecepatan clock yang sangat tinggi, keterlambatan ini dapat menjadi sangat besar dengan proses penjumlahan tidak diselesaikan dengan benar dalam satu siklus clock.
Waktu tunda yang tidak diinginkan ini disebut Propagasi Tunda. Juga masalah lain yang disebut "overflow" terjadi ketika penambah n-bit menambahkan dua angka paralel bersamaan yang jumlahnya lebih besar dari atau sama dengan 2n.
Salah satu solusinya adalah menghasilkan sinyal carry-input langsung dari input A dan B daripada menggunakan pengaturan riak di atas.
Ini kemudian menghasilkan jenis lain dari rangkaian penjumlahan biner yang disebut Carry Add Ahead Binary Adder di mana kecepatan penambah paralel dapat sangat ditingkatkan dengan menggunakan logika carry-look ahead.
Keuntungan dari carry look forward adders adalah bahwa lamanya waktu carry look forward adder perlu untuk menghasilkan JUMLAH yang benar tidak tergantung pada jumlah bit data yang digunakan dalam operasi, tidak seperti waktu siklus yang harus diselesaikan oleh penambah riak paralel. JUMLAH yang merupakan fungsi dari jumlah bit dalam addend.
Rangkaian penjumlahan penuh 4-bit dengan fitur look ahead atau lihat ke depan tersedia sebagai paket IC standar dalam bentuk penjumlahan biner TTL 4-bit 74LS83 atau 74LS283 dan CMOS 4008 yang dapat menambahkan dua nomor biner 4-bit dan menghasilkan JUMLAH dan output CARRY seperti yang ditunjukkan.
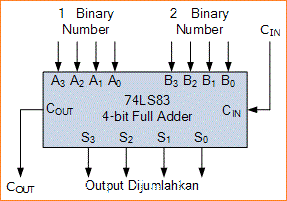
Dalam bentuknya yang paling dasar, penjumlahan dapat dibuat dari menghubungkan bersama gerbang Exclusive-OR dengan gerbang AND untuk menghasilkan rangkaian Penjumlahan Setengah (Half Adder). Dua setengah penjumlahan dapat digabungkan untuk menghasilkan Penjumlahan Penuh (Full Adder).
Ada sejumlah IC full-adder 4-bit yang tersedia seperti 74LS283 dan CD4008. yang akan menambahkan dua angka biner 4-bit dan memberikan bit carry input tambahan, serta bit carry output.
Sehingga Anda dapat mengalirkannya bersama-sama untuk menghasilkan 8-bit, 12-bit, 16-bit, penjumlahan tetapi propagasi carry keterlambatan bisa menjadi masalah utama dalam penjumlahan riak n-bit besar.
Rangkaian logika kombinasional umum dan sangat berguna lainnya yang dapat dibangun menggunakan hanya beberapa gerbang logika dasar yang memungkinkannya untuk menambahkan bersama dua atau lebih angka biner adalah Penjumlahan Bilangan Biner.
Sebuah rangkaian penjumlahan biner dasar dapat dibuat dari standar gerbang AND dan gerbang Ex-OR memungkinkan kita untuk “menambahkan” bersama-sama dua angka biner tunggal bit, A dan B.
Penjumlahan dua digit ini menghasilkan output yang disebut JUMLAH dari penjumlahan dan output kedua disebut bit CARRY atau Carry-out, (COUT) sesuai dengan aturan untuk penjumlahan biner.
Salah satu kegunaan utama untuk Penjumlahan Bilangan Biner adalah dalam rangkaian hitung dan penghitungan. Pertimbangkan penjumlahan sederhana dari dua nomor denary (base 10) di bawah ini.
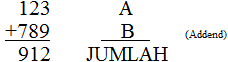
Dari pelajaran matematika kita di sekolah, kita belajar bahwa setiap kolom angka ditambahkan bersama-sama mulai dari sisi kanan dan bahwa setiap digit memiliki nilai tertimbang tergantung pada posisinya di dalam kolom.
Ketika setiap kolom ditambahkan bersama-sama, sebuah carry dihasilkan jika hasilnya lebih besar atau sama dengan 10, angka dasar. Carry ini kemudian ditambahkan ke hasil penjumlahan kolom berikutnya ke kiri dan seterusnya, penjumlahan matematika sekolah sederhana, tambahkan angka dan bawa.
Menambahkan bilangan biner adalah ide yang sama persis dengan penjumlahan bilangan desimal tetapi kali ini carry hanya dihasilkan ketika hasil di kolom mana pun lebih besar atau sama dengan "2", angka dasar dari biner. Dengan kata lain 1 + 1 menciptakan carry.
Penjumlahan Bilangan Biner
Penjumlahan Bilangan Biner mengikuti aturan dasar yang sama seperti untuk penjumlahan denary di atas kecuali dalam biner hanya ada dua digit dengan digit terbesar adalah "1".Jadi ketika menambahkan bilangan biner, suatu hasil dihasilkan ketika "JUMLAH" sama dengan atau lebih besar dari dua (1 +1) dan ini menjadi bit "CARRY" untuk setiap penjumlahan berikutnya yang diteruskan ke kolom berikutnya untuk penjumlahan dan seterusnya di. Pertimbangkan penjumlahan bit tunggal di bawah ini.
Penjumlahan Bilangan Biner dari Dua Bit
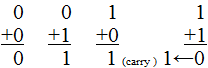
Ketika dua bit tunggal, A dan B ditambahkan bersama-sama, penjumlahan "0 + 0", "0 + 1" dan "1 + 0" menghasilkan "0" atau "1" hingga Anda mencapai Kolom terakhir "1 + 1" maka jumlahnya sama dengan "2". Tetapi nomor dua tidak ada dalam biner, 2 dalam biner sama dengan 10 , dengan kata lain nol untuk jumlah plus sedikit carry bit.
Maka pengoperasian penjumlahan sederhana memerlukan dua input data yang menghasilkan dua output, jumlah (S) dari persamaan dan bit Carry (C) seperti yang ditunjukkan.
Diagram Blok Penjumlahan Bilangan Biner

Untuk masalah penjumlahan 1-bit sederhana di atas, carry bit yang dihasilkan dapat diabaikan tetapi Anda mungkin telah memperhatikan hal lain sehubungan dengan penjumlahan dua bit ini, jumlah penjumlahan binernya menyerupai Gerbang Exclusive-OR.
Jika kita memberi label dua bit sebagai A dan B maka tabel kebenaran yang dihasilkan adalah jumlah dari dua bit tetapi tanpa carry final.
2-input Gerbang Exclusive-OR

Kita dapat melihat dari tabel kebenaran di atas, bahwa gerbang Exclusive-OR hanya menghasilkan output "1" ketika salah satu input berada pada logika "1", tetapi tidak keduanya sama dengan penjumlahan biner dari dua bit sebelumnya.
Namun untuk melakukan penjumlahan dua angka, mikroprosesor dan kalkulator elektronik memerlukan bit carry tambahan untuk menghitung persamaan dengan benar sehingga kita perlu menulis ulang penjumlahan sebelumnya untuk memasukkan dua-bit data output seperti yang ditunjukkan di bawah ini.
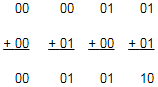
Dari persamaan di atas kita sekarang tahu bahwa gerbang Exclusive-OR hanya akan menghasilkan output "1" ketika input "ANTARA" berada pada logika "1", jadi kita membutuhkan output tambahan untuk menghasilkan bit carry ketika "KEDUA" input A dan B berada pada logika "1".
Satu gerbang digital yang pas dengan tagihan menghasilkan output "1" ketika kedua input A dan B adalah "1" (TINGGI) adalah standar Gerbang AND.
2-input Gerbang AND

Dengan menggabungkan gerbang Exclusive-OR dengan gerbang AND menghasilkan rangkaian penjumlahan biner digital sederhana yang umumnya dikenal sebagai rangkaian setengah penjumlahan atau "Half Adder".
Rangkaian Setengah Penjumlahan Bilangan Biner (half adder)
Setengah penjumlahan adalah rangkaian logika yang melakukan operasi tambahan pada dua digit biner. Setengah penjumlahan menghasilkan jumlah dan nilai tercatat yang keduanya merupakan digit biner.Tabel Kebenaran Setengah Penjumlahan dengan Carry-Out

Dari tabel kebenaran setengah penjumlahan kita dapat melihat bahwa output JUMLAH ( S ) adalah hasil dari gerbang Exclusive-OR dan Carry-out ( Cout ) adalah hasil dari gerbang AND. Maka ekspresi Boolean untuk setengah penjumlahan adalah sebagai berikut.
Untuk bit JUMLAH :
JUMLAH = A XOR B = A ⊕ B
Untuk bit CARRY:
CARRY = A AND B = AB
Salah satu kelemahan utama dari rangkaian Half Adder ketika digunakan sebagai penjumlahan biner, adalah bahwa tidak ada ketentuan untuk "Carry-in" dari rangkaian sebelumnya ketika menambahkan bersama beberapa bit data.
Sebagai contoh, misalkan kita ingin menambahkan dua byte data 8-bit, bit carry apa pun yang dihasilkan harus dapat "beriak" atau bergerak melintasi pola bit mulai dari bit paling tidak signifikan (LSB).
Operasi yang paling rumit yang dapat dilakukan setengah penjumlahan adalah "1+1" tetapi karena setengah penjumlahan tidak memiliki input carry, nilai tambah yang dihasilkan akan salah. Salah satu cara sederhana untuk mengatasi masalah ini adalah dengan menggunakan rangkaian penjumlahan tipe biner Full Adder.
Rangkaian Penjumlahan Penuh (full adder)
Perbedaan utama antara Full Adder dan Half Adder sebelumnya adalah bahwa full adder memiliki tiga input. Dua data bit tunggal yang sama input A dan B seperti sebelumnya ditambah input Carry-in ( C-in ) tambahan untuk menerima carry dari tahap sebelumnya seperti yang ditunjukkan di bawah ini.Diagram Blok Penjumlahan Penuh (full adder)

Kemudian penjumlahan penuh adalah rangkaian logika yang melakukan operasi tambahan pada tiga digit biner dan seperti penjumlahan setengah, itu juga menghasilkan melaksanakan ke kolom tambahan berikutnya.
Maka Carry-in adalah carry yang mungkin dari digit yang kurang signifikan, sementara Carry-out mewakili carry ke digit yang lebih signifikan.
Dalam banyak hal, penjumlahan penuh dapat dianggap sebagai dua penjumlahan setengah terhubung bersama-sama, dengan penjumlahan babak pertama meneruskan tugasnya ke penjumlahan babak kedua seperti yang ditunjukkan.
Diagram Logika Penjumlahan Bilangan Biner (full adder)

Karena rangkaian penjumlahan penuh di atas pada dasarnya adalah dua setengah pembahan yang terhubung bersama, tabel kebenaran untuk penjumlahan penuh mencakup kolom tambahan untuk memperhitungkan input Carry-in, CIN serta output yang dijumlahkan, S dan Carry-out , COUT bit.
Tabel Kebenaran Penjumlahan Bilangan Biner dengan Carry

Maka ekspresi Boolean untuk penjumlahan penuh adalah sebagai berikut.
Untuk bit JUMLAH ( S ):
JUMLAH = (A XOR B) AND XOR = (A ⊕ B) ⊕ Cin
Untuk bit CARRY-OUT ( Cout ):
CARRY-OUT = A AND B OR Cin (A XOR B) = AB + Cin (A ⊕ B)
Penjumlahan Bilangan Biner n-bit
Kita telah melihat di atas bahwa penjumlahan biner 1-bit tunggal dapat dibangun dari gerbang logika dasar. Tetapi bagaimana jika kita ingin menambahkan dua angka n-bit, maka n angka dari 1-bit Penjumlahan Penuh harus dihubungkan atau "cascaded" bersama untuk menghasilkan apa yang dikenal sebagai Ripple Carry Adder.Ripple Carry Adder sebuah "n", full adder 1-bit yang di-cascade bersama dengan tiap full adder dan kemudian akan mewakili kolom tunggal tertimbang pada adder biner yang panjang.
Ini disebut adder ripple carry karena sinyal carry menghasilkan efek "ripple" melalui penjumlahan biner dari kanan ke kiri, (LSB ke MSB).
Sebagai contoh, misalkan kita ingin "menambahkan" bersama dua angka 4-bit, dua output dari penjumlahan penuh pertama akan memberikan jumlah digit tempat pertama ( S ) dari penjumlahan ditambah bit carry-out yang bertindak sebagai carry dalam digit penjumlahan biner berikutnya.
Penjumlahan biner kedua dalam rantai juga menghasilkan output yang dijumlahkan (bit ke-2) ditambah bit carry-out lainnya dan kita dapat terus menambahkan lebih banyak penjumlahan penuh pada kombinasi untuk menambahkan angka yang lebih besar, menghubungkan output bit carry dari penjumlahan biner penuh pertama ke penjumlahan penuh berikutnya, dan sebagainya.
Contoh dari penjumlahan 4-bit diberikan di bawah ini.
4-bit Ripple Carry Adder

Salah satu kelemahan utama dari “cascading” bersama-sama 1-bit penjumlahan biner untuk menambah angka biner yang besar adalah bahwa jika input A dan B berubah, jumlah pada outputnya tidak akan valid sampai semua carry-input telah “rippled” melalui setiap penjumlahan penuh di rantai karena MSB (bit paling signifikan) dari jumlah harus menunggu perubahan dari input carry LSB (bit kurang signifikan).
Akibatnya, akan ada penundaan yang terbatas sebelum output dari penambah menanggapi setiap perubahan dalam inputnya yang menghasilkan penundaan akumulasi.
Ketika ukuran bit yang ditambahkan tidak terlalu besar misalnya, 4 atau 8 bit, atau kecepatan penjumlahan dari penambah tidak penting, penundaan ini mungkin tidak penting.
Namun, ketika ukuran bit lebih besar misalnya 32 atau 64 bit yang digunakan dalam penjumlahan multi-bit, atau penjumlahan diperlukan pada kecepatan clock yang sangat tinggi, keterlambatan ini dapat menjadi sangat besar dengan proses penjumlahan tidak diselesaikan dengan benar dalam satu siklus clock.
Waktu tunda yang tidak diinginkan ini disebut Propagasi Tunda. Juga masalah lain yang disebut "overflow" terjadi ketika penambah n-bit menambahkan dua angka paralel bersamaan yang jumlahnya lebih besar dari atau sama dengan 2n.
Salah satu solusinya adalah menghasilkan sinyal carry-input langsung dari input A dan B daripada menggunakan pengaturan riak di atas.
Ini kemudian menghasilkan jenis lain dari rangkaian penjumlahan biner yang disebut Carry Add Ahead Binary Adder di mana kecepatan penambah paralel dapat sangat ditingkatkan dengan menggunakan logika carry-look ahead.
Keuntungan dari carry look forward adders adalah bahwa lamanya waktu carry look forward adder perlu untuk menghasilkan JUMLAH yang benar tidak tergantung pada jumlah bit data yang digunakan dalam operasi, tidak seperti waktu siklus yang harus diselesaikan oleh penambah riak paralel. JUMLAH yang merupakan fungsi dari jumlah bit dalam addend.
Rangkaian penjumlahan penuh 4-bit dengan fitur look ahead atau lihat ke depan tersedia sebagai paket IC standar dalam bentuk penjumlahan biner TTL 4-bit 74LS83 atau 74LS283 dan CMOS 4008 yang dapat menambahkan dua nomor biner 4-bit dan menghasilkan JUMLAH dan output CARRY seperti yang ditunjukkan.
Simbol Logika 74LS83

Ringkasan Penjumlahan Bilangan Biner
Kita telah melihat dalam tutorial ini tentang Penjumlahan Bilangan Biner bahwa rangkaian penjumlahan dapat digunakan untuk "menambahkan" bersama dua angka biner yang menghasilkan "carry-out".Dalam bentuknya yang paling dasar, penjumlahan dapat dibuat dari menghubungkan bersama gerbang Exclusive-OR dengan gerbang AND untuk menghasilkan rangkaian Penjumlahan Setengah (Half Adder). Dua setengah penjumlahan dapat digabungkan untuk menghasilkan Penjumlahan Penuh (Full Adder).
Ada sejumlah IC full-adder 4-bit yang tersedia seperti 74LS283 dan CD4008. yang akan menambahkan dua angka biner 4-bit dan memberikan bit carry input tambahan, serta bit carry output.
Sehingga Anda dapat mengalirkannya bersama-sama untuk menghasilkan 8-bit, 12-bit, 16-bit, penjumlahan tetapi propagasi carry keterlambatan bisa menjadi masalah utama dalam penjumlahan riak n-bit besar.