Tegangan RMS
RMS atau nilai efektif dari bentuk gelombang sinusoidal memberikan efek pemanasan yang sama dari supply DC yang setara
Dalam tutorial kami tentang Gelombang AC kami melihat secara singkat nilai tegangan RMS dari bentuk gelombang sinusoidal dan mengatakan bahwa nilai RMS ini memberikan efek pemanasan yang sama dengan daya DC yang setara dan dalam tutorial ini kita akan memperluas teori ini sedikit lagi dengan melihat pada tegangan RMS dan arus lebih detail.
Istilah "RMS" adalah singkatan dari "Root-Mean-Squared". Sebagian besar buku mendefinisikan ini sebagai "jumlah daya AC yang menghasilkan efek pemanasan yang sama dengan daya DC yang setara", atau sesuatu yang serupa di sepanjang garis ini, tetapi nilai RMS lebih dari itu.
Nilai RMS adalah akar kuadrat dari nilai rata-rata (mean) dari fungsi kuadrat dari nilai instan. Simbol yang digunakan untuk mendefinisikan nilai RMS adalah VRMS atau IRMS. Nilai RMS, HANYA mengacu pada tegangan sinusoidal yang bervariasi waktu, arus atau bentuk gelombang yang kompleks adalah besarnya perubahan bentuk gelombang dari waktu ke waktu dan tidak digunakan dalam analisis atau perhitungan rangkaian DC karena besarnya selalu konstan.
Ketika digunakan untuk membandingkan nilai tegangan RMS yang setara dari gelombang sinusoidal bolak-balik yang memasok daya listrik yang sama ke beban yang diberikan sebagai rangkaian DC yang setara, nilai RMS disebut "nilai efektif" dan umumnya disajikan sebagai: Veff atau Ieff.
Dengan kata lain, nilai efektif adalah nilai DC ekuivalen yang memberi tahu Anda berapa volt atau ampli DC yang bentuk gelombang sinusoidal yang memvariasikan sama dengan waktu dalam hal kemampuannya menghasilkan daya yang sama.

Jadi bagaimana kita menghitung Tegangan RMS dari bentuk gelombang sinusoidal. Tegangan RMS dari bentuk gelombang sinusoidal atau kompleks dapat ditentukan dengan dua metode dasar.
Setengah positif dari gelombang dibagi menjadi sejumlah "n" bagian yang sama atau mid-ordinate dan semakin banyak mid-ordinate yang ditarik sepanjang gelombang, semakin akurat akan menjadi hasil akhir. Lebar setiap pertengahan ordinat akan menjadi n° derajat dan tinggi setiap pertengahan ordinat akan sama dengan nilai sesaat dari bentuk gelombang pada waktu itu sepanjang sumbu-x bentuk gelombang.

Setiap nilai tengah-ordinat dari suatu bentuk gelombang (bentuk gelombang tegangan dalam kasus ini) dikalikan dengan sendirinya (kuadrat) dan ditambahkan ke yang berikutnya. Metode ini memberi kita bagian "kuadrat" atau Kuadrat dari ekspresi tegangan RMS.
Berikutnya nilai kuadrat ini dibagi dengan jumlah mid-ordinate yang digunakan untuk memberi kita bagian Mean dari ekspresi tegangan RMS, dan dalam contoh sederhana kami di atas jumlah mid-ordinate yang digunakan adalah dua belas (12). Akhirnya, akar kuadrat dari hasil sebelumnya ditemukan memberi kita bagian Root dari tegangan RMS.
Kemudian kita bisa mendefinisikan istilah yang digunakan untuk menggambarkan tegangan rms ( VRMS ) sebagai “kuadrat akar dari rata-rata dari kuadrat dari pertengahan-koordinat dari bentuk gelombang tegangan” dan ini diberikan sebagai:

dan untuk contoh sederhana kami di atas, tegangan RMS akan dihitung sebagai:

Jadi mari kita asumsikan bahwa tegangan bolak-balik memiliki tegangan puncak ( Vpk ) 20 volt dan dengan mengambil 10 nilai pertengahan-ordinasi ditemukan bervariasi selama satu setengah siklus sebagai berikut:
Tegangan RMS karena itu dihitung sebagai:
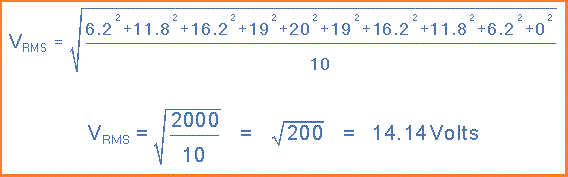
Kemudian nilai Tegangan RMS menggunakan metode grafis dihasilkan adalah: 14,14 Volt .
Namun, ketika berhadapan dengan bentuk gelombang sinusoidal murni kita dapat membuatnya sedikit lebih mudah bagi diri kita sendiri dengan menggunakan cara analitis atau matematis untuk menemukan nilai RMS.
Sebuah tegangan sinusoidal periodik adalah konstan dan dapat didefinisikan sebagai V(t) = Vmax*cos (ωt) dengan periode T. Kemudian kita dapat menghitung nilai root-mean-square (rms) dari tegangan sinusoidal ( V(t) ) sebagai:

Mengintegrasikan melalui batas yang diambil dari 0 hingga 360° atau "T", periode tersebut memberikan:
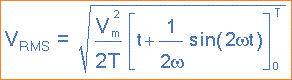
Di mana: Vm adalah nilai puncak atau maksimum dari bentuk gelombang. Dibagi lebih jauh dengan ω = 2π/T, persamaan kompleks di atas akhirnya berkurang juga:
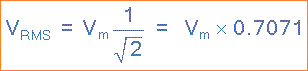
Kemudian tegangan RMS ( VRMS ) dari bentuk gelombang sinusoidal ditentukan dengan mengalikan nilai tegangan puncak dengan 0.7071, yang sama dengan yang dibagi dengan akar kuadrat dari dua ( 1/√2 ). Tegangan RMS, yang juga dapat disebut sebagai nilai efektif, tergantung pada besarnya bentuk gelombang dan bukan merupakan fungsi baik frekuensi bentuk gelombang maupun sudut fasa.
Dari contoh grafis di atas, tegangan puncak ( Vpk ) dari bentuk gelombang diberikan sebagai 20 Volt. Dengan menggunakan metode analitis yang baru saja ditentukan kita dapat menghitung tegangan RMS sebagai:
VRMS = Vpk * 0.7071 = 20 x 0.7071 = 14.14V
Perhatikan bahwa nilai 14.14 volt ini adalah nilai yang sama dengan metode grafis sebelumnya. Kemudian kita dapat menggunakan metode grafis mid-ordinate, atau metode perhitungan analitik untuk menemukan tegangan RMS atau nilai arus dari bentuk gelombang sinusoidal.
Perhatikan bahwa mengalikan nilai puncak atau maksimum dengan konstanta 0.7071, HANYA berlaku untuk bentuk gelombang sinusoidal. Untuk bentuk gelombang non-sinusoidal, metode grafis harus digunakan. Tetapi selain menggunakan nilai puncak atau maksimum dari sinusoidal, kita juga dapat menggunakan nilai puncak-ke-puncak ( VP-P ) atau nilai rata-rata ( VAVG ) untuk menemukan nilai kuadrat rata-rata setara akar sinusoidal seperti yang ditunjukkan:

Salah satu cara mudah adalah dengan menggunakan nilai puncak untuk bentuk gelombang. Metode umum lainnya adalah dengan menggunakan nilai efektif yang juga dikenal dengan ekspresi yang lebih umum dari Root Mean Square atau hanya nilai RMS.
Akar rata-rata kuadrat, nilai RMS sinusoidal tidak sama dengan rata-rata semua nilai sesaat. Rasio nilai RMS tegangan terhadap nilai maksimum tegangan sama dengan rasio nilai RMS arus terhadap nilai maksimum arus.
Kebanyakan alat ukur listrik multimeter, baik voltmeter atau amperemeter, mengukur nilai RMS dengan asumsi bentuk gelombang sinusoidal murni. Untuk menemukan nilai RMS dari gelombang non-sinusoidal diperlukan "True RMS Multimeter".
Nilai RMS dari gelombang sinusoidal memberikan efek pemanasan yang sama dengan arus DC dengan nilai yang sama. Itu adalah jika arus searah, I melewati resistansi R ohm, daya DC yang dikonsumsi oleh resistor karena panas akan menjadi I2R watt. Kemudian jika arus bolak-balik, i = Imax*sinθ mengalir melalui resistansi yang sama, daya AC yang dikonversi menjadi panas adalah: I2rms*R watt.
Kemudian ketika berhadapan dengan tegangan dan arus bolak-balik, arus harus diperlakukan sebagai nilai RMS kecuali dinyatakan lain. Oleh karena itu arus bolak-balik 10 ampere akan memiliki efek pemanasan yang sama dengan arus searah 10 ampere dan nilai maksimum 14,14 ampere.
Setelah sekarang menentukan nilai RMS dari tegangan gelombang bolak-balik (atau arus), dalam tutorial berikutnya kita akan melihat perhitungan Tegangan Rata-rata, VAVG dari tegangan bolak-balik dan kemudian membandingkan keduanya.
Dalam tutorial kami tentang Gelombang AC kami melihat secara singkat nilai tegangan RMS dari bentuk gelombang sinusoidal dan mengatakan bahwa nilai RMS ini memberikan efek pemanasan yang sama dengan daya DC yang setara dan dalam tutorial ini kita akan memperluas teori ini sedikit lagi dengan melihat pada tegangan RMS dan arus lebih detail.
Istilah "RMS" adalah singkatan dari "Root-Mean-Squared". Sebagian besar buku mendefinisikan ini sebagai "jumlah daya AC yang menghasilkan efek pemanasan yang sama dengan daya DC yang setara", atau sesuatu yang serupa di sepanjang garis ini, tetapi nilai RMS lebih dari itu.
Nilai RMS adalah akar kuadrat dari nilai rata-rata (mean) dari fungsi kuadrat dari nilai instan. Simbol yang digunakan untuk mendefinisikan nilai RMS adalah VRMS atau IRMS. Nilai RMS, HANYA mengacu pada tegangan sinusoidal yang bervariasi waktu, arus atau bentuk gelombang yang kompleks adalah besarnya perubahan bentuk gelombang dari waktu ke waktu dan tidak digunakan dalam analisis atau perhitungan rangkaian DC karena besarnya selalu konstan.
Ketika digunakan untuk membandingkan nilai tegangan RMS yang setara dari gelombang sinusoidal bolak-balik yang memasok daya listrik yang sama ke beban yang diberikan sebagai rangkaian DC yang setara, nilai RMS disebut "nilai efektif" dan umumnya disajikan sebagai: Veff atau Ieff.
Dengan kata lain, nilai efektif adalah nilai DC ekuivalen yang memberi tahu Anda berapa volt atau ampli DC yang bentuk gelombang sinusoidal yang memvariasikan sama dengan waktu dalam hal kemampuannya menghasilkan daya yang sama.
Tegangan RMS Ekuivalen (setara)

Jadi bagaimana kita menghitung Tegangan RMS dari bentuk gelombang sinusoidal. Tegangan RMS dari bentuk gelombang sinusoidal atau kompleks dapat ditentukan dengan dua metode dasar.
- Metode Grafis - yang dapat digunakan untuk menemukan nilai RMS dari setiap bentuk gelombang waktu non-sinusoidal dengan menggambar sejumlah mid-ordinate ke dalam bentuk gelombang.
- Metode Analitik - adalah prosedur matematika untuk menemukan nilai efektif atau RMS dari setiap tegangan atau arus periodik menggunakan kalkulus.
Metode Grafis Tegangan RMS
Sementara metode perhitungannya sama untuk kedua bagian bentuk gelombang AC, untuk contoh ini kita hanya akan mempertimbangkan setengah siklus positif. Nilai efektif atau rms dari suatu gelombang dapat ditemukan dengan jumlah akurasi yang masuk akal dengan mengambil nilai instan spasi yang sama di sepanjang bentuk gelombang.Setengah positif dari gelombang dibagi menjadi sejumlah "n" bagian yang sama atau mid-ordinate dan semakin banyak mid-ordinate yang ditarik sepanjang gelombang, semakin akurat akan menjadi hasil akhir. Lebar setiap pertengahan ordinat akan menjadi n° derajat dan tinggi setiap pertengahan ordinat akan sama dengan nilai sesaat dari bentuk gelombang pada waktu itu sepanjang sumbu-x bentuk gelombang.
Metode Grafis

Setiap nilai tengah-ordinat dari suatu bentuk gelombang (bentuk gelombang tegangan dalam kasus ini) dikalikan dengan sendirinya (kuadrat) dan ditambahkan ke yang berikutnya. Metode ini memberi kita bagian "kuadrat" atau Kuadrat dari ekspresi tegangan RMS.
Berikutnya nilai kuadrat ini dibagi dengan jumlah mid-ordinate yang digunakan untuk memberi kita bagian Mean dari ekspresi tegangan RMS, dan dalam contoh sederhana kami di atas jumlah mid-ordinate yang digunakan adalah dua belas (12). Akhirnya, akar kuadrat dari hasil sebelumnya ditemukan memberi kita bagian Root dari tegangan RMS.
Kemudian kita bisa mendefinisikan istilah yang digunakan untuk menggambarkan tegangan rms ( VRMS ) sebagai “kuadrat akar dari rata-rata dari kuadrat dari pertengahan-koordinat dari bentuk gelombang tegangan” dan ini diberikan sebagai:

dan untuk contoh sederhana kami di atas, tegangan RMS akan dihitung sebagai:

Jadi mari kita asumsikan bahwa tegangan bolak-balik memiliki tegangan puncak ( Vpk ) 20 volt dan dengan mengambil 10 nilai pertengahan-ordinasi ditemukan bervariasi selama satu setengah siklus sebagai berikut:
Tegangan
|
6.2V
|
11.8V
|
16.2V
|
19.0V
|
20.0V
|
19.0V
|
16.2V
|
11.8V
|
6.2V
|
0V
|
Sudut
|
18°
|
36°
|
54°
|
72°
|
90°
|
108°
|
126°
|
144°
|
162°
|
180°
|
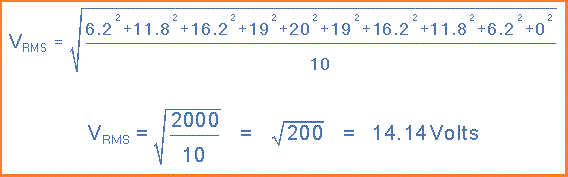
Kemudian nilai Tegangan RMS menggunakan metode grafis dihasilkan adalah: 14,14 Volt .
Metode Analitik Tegangan RMS
Metode grafis di atas adalah cara yang sangat baik untuk menemukan tegangan (atau arus) efektif atau RMS, dari bentuk gelombang bolak-balik yang tidak simetris atau sinusoidal. Dengan kata lain bentuk gelombang menyerupai bentuk gelombang yang kompleks.Namun, ketika berhadapan dengan bentuk gelombang sinusoidal murni kita dapat membuatnya sedikit lebih mudah bagi diri kita sendiri dengan menggunakan cara analitis atau matematis untuk menemukan nilai RMS.
Sebuah tegangan sinusoidal periodik adalah konstan dan dapat didefinisikan sebagai V(t) = Vmax*cos (ωt) dengan periode T. Kemudian kita dapat menghitung nilai root-mean-square (rms) dari tegangan sinusoidal ( V(t) ) sebagai:

Mengintegrasikan melalui batas yang diambil dari 0 hingga 360° atau "T", periode tersebut memberikan:
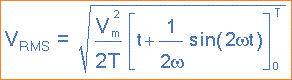
Di mana: Vm adalah nilai puncak atau maksimum dari bentuk gelombang. Dibagi lebih jauh dengan ω = 2π/T, persamaan kompleks di atas akhirnya berkurang juga:
Persamaan Tegangan RMS
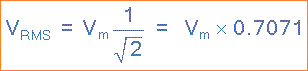
Kemudian tegangan RMS ( VRMS ) dari bentuk gelombang sinusoidal ditentukan dengan mengalikan nilai tegangan puncak dengan 0.7071, yang sama dengan yang dibagi dengan akar kuadrat dari dua ( 1/√2 ). Tegangan RMS, yang juga dapat disebut sebagai nilai efektif, tergantung pada besarnya bentuk gelombang dan bukan merupakan fungsi baik frekuensi bentuk gelombang maupun sudut fasa.
Dari contoh grafis di atas, tegangan puncak ( Vpk ) dari bentuk gelombang diberikan sebagai 20 Volt. Dengan menggunakan metode analitis yang baru saja ditentukan kita dapat menghitung tegangan RMS sebagai:
VRMS = Vpk * 0.7071 = 20 x 0.7071 = 14.14V
Perhatikan bahwa nilai 14.14 volt ini adalah nilai yang sama dengan metode grafis sebelumnya. Kemudian kita dapat menggunakan metode grafis mid-ordinate, atau metode perhitungan analitik untuk menemukan tegangan RMS atau nilai arus dari bentuk gelombang sinusoidal.
Perhatikan bahwa mengalikan nilai puncak atau maksimum dengan konstanta 0.7071, HANYA berlaku untuk bentuk gelombang sinusoidal. Untuk bentuk gelombang non-sinusoidal, metode grafis harus digunakan. Tetapi selain menggunakan nilai puncak atau maksimum dari sinusoidal, kita juga dapat menggunakan nilai puncak-ke-puncak ( VP-P ) atau nilai rata-rata ( VAVG ) untuk menemukan nilai kuadrat rata-rata setara akar sinusoidal seperti yang ditunjukkan:
Nilai RMS Sinusoidal

Ringkasan Tegangan RMS
Kemudian untuk meringkas. Ketika berhadapan dengan tegangan (atau arus) bolak-balik kita dihadapkan dengan masalah bagaimana kita merepresentasikan tegangan atau besarnya sinyal.Salah satu cara mudah adalah dengan menggunakan nilai puncak untuk bentuk gelombang. Metode umum lainnya adalah dengan menggunakan nilai efektif yang juga dikenal dengan ekspresi yang lebih umum dari Root Mean Square atau hanya nilai RMS.
Akar rata-rata kuadrat, nilai RMS sinusoidal tidak sama dengan rata-rata semua nilai sesaat. Rasio nilai RMS tegangan terhadap nilai maksimum tegangan sama dengan rasio nilai RMS arus terhadap nilai maksimum arus.
Kebanyakan alat ukur listrik multimeter, baik voltmeter atau amperemeter, mengukur nilai RMS dengan asumsi bentuk gelombang sinusoidal murni. Untuk menemukan nilai RMS dari gelombang non-sinusoidal diperlukan "True RMS Multimeter".
Nilai RMS dari gelombang sinusoidal memberikan efek pemanasan yang sama dengan arus DC dengan nilai yang sama. Itu adalah jika arus searah, I melewati resistansi R ohm, daya DC yang dikonsumsi oleh resistor karena panas akan menjadi I2R watt. Kemudian jika arus bolak-balik, i = Imax*sinθ mengalir melalui resistansi yang sama, daya AC yang dikonversi menjadi panas adalah: I2rms*R watt.
Kemudian ketika berhadapan dengan tegangan dan arus bolak-balik, arus harus diperlakukan sebagai nilai RMS kecuali dinyatakan lain. Oleh karena itu arus bolak-balik 10 ampere akan memiliki efek pemanasan yang sama dengan arus searah 10 ampere dan nilai maksimum 14,14 ampere.
Setelah sekarang menentukan nilai RMS dari tegangan gelombang bolak-balik (atau arus), dalam tutorial berikutnya kita akan melihat perhitungan Tegangan Rata-rata, VAVG dari tegangan bolak-balik dan kemudian membandingkan keduanya.