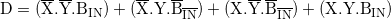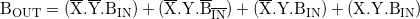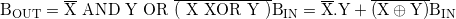Pengurangan Bilangan Biner
Pengurangan Bilangan Biner adalah jenis lain dari rangkaian aritmatika kombinasional yang menghasilkan output yang merupakan pengurangan dari dua bilangan biner.
Seperti namanya, Pengurangan Bilangan Biner adalah rangkaian pengambilan keputusan yang mengurangi dua angka biner dari satu sama lain, misalnya, X - Y untuk menemukan perbedaan yang dihasilkan antara kedua angka.
Berbeda dengan Penjumlahan Bilangan Biner yang menghasilkan JUMLAH dan CARRY bit ketika dua angka biner ditambahkan bersamaan, pengurangan bilangan biner menghasilkan PERBEDAAN, D dengan menggunakan bit BORROW, B dari kolom sebelumnya. Maka jelas, operasi pengurangan adalah kebalikan dari penjumlahan.
Kita belajar dari pelajaran matematika di sekolah bahwa tanda minus, “ - ” digunakan untuk perhitungan pengurangan, dan ketika satu angka dikurangkan dari yang lain, pinjaman diperlukan jika pengurang (substrahend) lebih besar dari yang dikurangi (minuend). Pertimbangkan pengurangan sederhana dari dua angka denary (base 10) di bawah ini.
Kita tidak bisa langsung mengurangi 8 dari 3 di kolom pertama karena 8 lebih besar dari 3, jadi kita harus meminjam 10, angka dasar, dari kolom berikutnya dan menambahkannya ke minuend untuk menghasilkan 13 dikurangi 8.
Ini “dipinjam ”10 kemudian kembali ke subtrahend kolom berikutnya setelah perbedaan ditemukan. Matematika sekolah sederhana, pinjam 10 jika perlu, temukan perbedaannya dan kembalikan pinjaman.
Pengurangan satu nomor biner dari yang lain adalah ide yang persis sama dengan yang untuk mengurangi dua angka desimal tetapi karena sistem angka biner adalah sistem penomoran Base-2 yang menggunakan 0 dan 1 sebagai dua digit independennya, biner yang besar angka-angka yang harus dikurangkan dari satu sama yang lain oleh karena itu diwakili dalam hal "0" dan "1".
Mengurangkan "1" dari "1" menghasilkan "0", tetapi mengurangi "1" dari "0" membutuhkan pinjaman. Dengan kata lain 0 - 1 membutuhkan pinjaman.
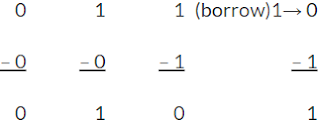
Untuk masalah pengurangan 1-bit sederhana di atas, jika bit pinjaman diabaikan, hasil pengurangan bilangan binernya menyerupai Gerbang Exclusive-OR. Untuk mencegah kebingungan dalam tutorial ini antara input pengurangan bilangan biner berlabel, B dan output bit pinjaman yang dihasilkan dari pengurangan bilangan biner juga diberi label, B.
Kami akan memberi label dua bit input sebagai X untuk minuend dan Y untuk subtrahend. Kemudian tabel kebenaran yang dihasilkan adalah perbedaan antara dua bit input dari pengurang biner tunggal diberikan sebagai:
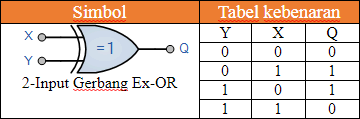
Seperti dengan Penjumlahan Bilangan Biner, perbedaan antara dua digit hanya "1" ketika dua input ini tidak sama dengan yang diberikan oleh ekspresi Gerbang Exclusive-OR (Ex-OR).
Namun, kami membutuhkan output tambahan untuk menghasilkan bit pinjaman ketika input X = 0 dan Y = 1. Sayangnya tidak ada gerbang logika standar yang akan menghasilkan output untuk kombinasi input X dan Y ini.
Tetapi kita tahu bahwa Gerbang AND menghasilkan output “1” ketika kedua input X dan Y keduanya “1” (HIGH) jadi jika kita menggunakan inverter atau Gerbang NOT untuk melengkapi input X sebelum diumpankan ke gerbang AND, kita dapat menghasilkan output pinjaman yang diperlukan ketika X = 0 dan Y = 1 seperti yang ditunjukkan di bawah ini.
Kemudian dengan menggabungkan gerbang Exclusive-OR dengan kombinasi NOT-AND menghasilkan rangkaian pengurangan bilangan biner digital sederhana yang umumnya dikenal sebagai Pengurangan Setengah (Half Subtractor) seperti yang ditunjukkan.
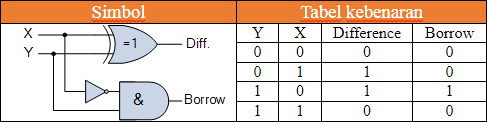
Dari tabel kebenaran setengah pengurangan kita dapat melihat bahwa output PERBEDAAN ( D ) adalah hasil dari gerbang Exclusive-OR dan Peminjam-out ( Bout ) adalah hasil dari kombinasi NOT-AND. Maka ekspresi Boolean untuk setengah pengurangan adalah sebagai berikut.
Untuk bit PERBEDAAN (Diff):
Untuk bit Peminjam (BORROW)
Jika kita membandingkan ekspresi Boolean dari setengah pengurang dengan setengah penambah, kita dapat melihat bahwa dua ekspresi untuk JUMLAH (penambah) dan PERBEDAAN (pengurang) persis sama dan karena itu seharusnya karena fungsi gerbang Exclusive-OR.
Dua ekspresi Boolean untuk pengurangan bilangan biner PEMINJAM juga sangat mirip dengan yang untuk CARRY adders. Kemudian semua yang diperlukan untuk mengkonversi setengah penambah untuk setengah pengurang adalah inversi dari input minuend X.
Salah satu kelemahan utama dari rangkaian Setengah Pengurangan ketika digunakan sebagai pengurangan bilangan biner, adalah bahwa tidak ada ketentuan untuk "Peminjam-in" dari rangkaian sebelumnya ketika mengurangi beberapa bit data dari satu sama lain.
Maka kita perlu menghasilkan apa yang disebut rangkaian "pengurang biner penuh" untuk memperhitungkan input pinjaman ini dari rangkaian sebelumnya.
Dua data bit tunggal input X (minuend) dan Y (subtrahend) sama seperti sebelumnya ditambah input peminjam atau Borrow-in ( B-in ) tambahan untuk menerima pinjaman yang dihasilkan oleh proses pengurangan dari tahap sebelumnya seperti yang ditunjukkan di bawah ini.
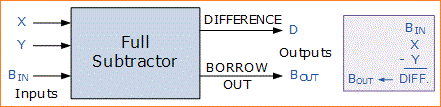
Kemudian rangkaian kombinasional dari "pengurangan penuh" melakukan operasi pengurangan pada tiga bit biner yang menghasilkan output untuk perbedaan D dan meminjam B-out.
Sama seperti rangkaian penjumlahan bilangan biner, pengurang penuh juga dapat dianggap sebagai dua pengurang setengah terhubung bersama-sama, dengan pengurang paruh pertama meneruskan pinjamannya ke pengurang paruh kedua sebagai berikut.
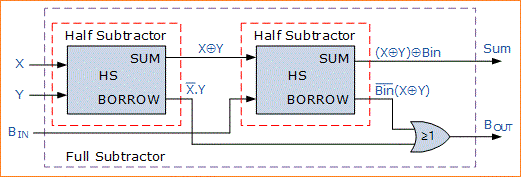
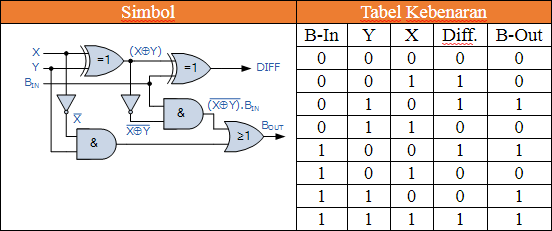
Sebagai rangkaian pengurang penuh atas merupakan dua Setengah Pengurangan mengalir bersama-sama, tabel kebenaran untuk pengurangan penuh akan memiliki delapan kombinasi input yang berbeda karena ada tiga variabel input, data bit dan Borrow-in, BIN input. Juga termasuk perbedaan output, D dan bit Borrow-out, BOUT.
Maka ekspresi Boolean untuk pengurangan penuh adalah sebagai berikut.
Untuk bit PERBEDAAN ( D ):
yang dapat disederhanakan juga:
Untuk bit BORROW OUT ( BOUT ):
yang juga akan menyederhanakan:
Misalnya dua angka biner 4-bit. Kami katakan sebelumnya bahwa satu-satunya perbedaan antara penambah penuh dan pengurang penuh adalah inversi dari salah satu input.
Jadi dengan menggunakan penjumlahan n-bit dan n jumlah inverter ( Gerbang NOT ), proses pengurangan menjadi tambahan karena kita dapat menggunakan notasi komplemen dua pada semua bit dalam subtrahend dan mengatur input carry dari bit yang paling tidak signifikan untuk logika "1" (TINGGI).
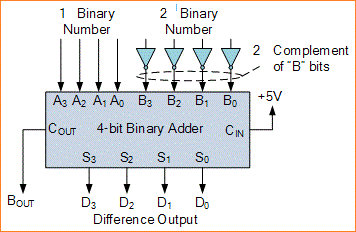
Kemudian kita dapat menggunakan IC full-adder 4-bit seperti 74LS283 dan CD4008 untuk melakukan pengurangan hanya dengan menggunakan komplemen dua pada subtrahend, input B sebagai X - Y sama dengan mengatakan, X + (-Y) yang sama dengan X ditambah komplemen Y untuk keduanya.
Jika kita ingin menggunakan penjumlahan 4-bit sebagai tambahan sekali lagi, yang perlu kita lakukan hanyalah mengatur carry-in ( CIN ) input RENDAH pada logika "0".
Karena kita dapat menggunakan IC penjumlah 4-bit seperti 74LS83 atau 74LS283 sebagai penjumlahan-penuh atau Pengurangan-penuh, mereka tersedia sebagai rangkaian penambah/pengurang tunggal dengan input kontrol tunggal untuk memilih antara dua operasi.
Seperti namanya, Pengurangan Bilangan Biner adalah rangkaian pengambilan keputusan yang mengurangi dua angka biner dari satu sama lain, misalnya, X - Y untuk menemukan perbedaan yang dihasilkan antara kedua angka.
Berbeda dengan Penjumlahan Bilangan Biner yang menghasilkan JUMLAH dan CARRY bit ketika dua angka biner ditambahkan bersamaan, pengurangan bilangan biner menghasilkan PERBEDAAN, D dengan menggunakan bit BORROW, B dari kolom sebelumnya. Maka jelas, operasi pengurangan adalah kebalikan dari penjumlahan.
Kita belajar dari pelajaran matematika di sekolah bahwa tanda minus, “ - ” digunakan untuk perhitungan pengurangan, dan ketika satu angka dikurangkan dari yang lain, pinjaman diperlukan jika pengurang (substrahend) lebih besar dari yang dikurangi (minuend). Pertimbangkan pengurangan sederhana dari dua angka denary (base 10) di bawah ini.
Kita tidak bisa langsung mengurangi 8 dari 3 di kolom pertama karena 8 lebih besar dari 3, jadi kita harus meminjam 10, angka dasar, dari kolom berikutnya dan menambahkannya ke minuend untuk menghasilkan 13 dikurangi 8.
Ini “dipinjam ”10 kemudian kembali ke subtrahend kolom berikutnya setelah perbedaan ditemukan. Matematika sekolah sederhana, pinjam 10 jika perlu, temukan perbedaannya dan kembalikan pinjaman.
Pengurangan satu nomor biner dari yang lain adalah ide yang persis sama dengan yang untuk mengurangi dua angka desimal tetapi karena sistem angka biner adalah sistem penomoran Base-2 yang menggunakan 0 dan 1 sebagai dua digit independennya, biner yang besar angka-angka yang harus dikurangkan dari satu sama yang lain oleh karena itu diwakili dalam hal "0" dan "1".
Pengurangan Bilangan Biner
Pengurangan Bilangan Biner dapat mengambil banyak bentuk tetapi aturan untuk pengurangan adalah sama dengan proses apa pun yang Anda gunakan. Karena notasi biner hanya memiliki dua digit, mengurangkan "0" dari "0" atau "1" membuat hasilnya tidak berubah seperti 0-0 = 0 dan 1-0 = 1.Mengurangkan "1" dari "1" menghasilkan "0", tetapi mengurangi "1" dari "0" membutuhkan pinjaman. Dengan kata lain 0 - 1 membutuhkan pinjaman.
Pengurangan Bilangan Biner dari 2-Bit
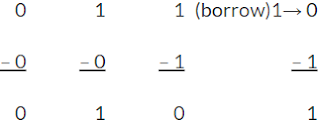
Untuk masalah pengurangan 1-bit sederhana di atas, jika bit pinjaman diabaikan, hasil pengurangan bilangan binernya menyerupai Gerbang Exclusive-OR. Untuk mencegah kebingungan dalam tutorial ini antara input pengurangan bilangan biner berlabel, B dan output bit pinjaman yang dihasilkan dari pengurangan bilangan biner juga diberi label, B.
Kami akan memberi label dua bit input sebagai X untuk minuend dan Y untuk subtrahend. Kemudian tabel kebenaran yang dihasilkan adalah perbedaan antara dua bit input dari pengurang biner tunggal diberikan sebagai:
2-input Gerbang Exclusive-OR
Seperti dengan Penjumlahan Bilangan Biner, perbedaan antara dua digit hanya "1" ketika dua input ini tidak sama dengan yang diberikan oleh ekspresi Gerbang Exclusive-OR (Ex-OR).
Namun, kami membutuhkan output tambahan untuk menghasilkan bit pinjaman ketika input X = 0 dan Y = 1. Sayangnya tidak ada gerbang logika standar yang akan menghasilkan output untuk kombinasi input X dan Y ini.
Tetapi kita tahu bahwa Gerbang AND menghasilkan output “1” ketika kedua input X dan Y keduanya “1” (HIGH) jadi jika kita menggunakan inverter atau Gerbang NOT untuk melengkapi input X sebelum diumpankan ke gerbang AND, kita dapat menghasilkan output pinjaman yang diperlukan ketika X = 0 dan Y = 1 seperti yang ditunjukkan di bawah ini.
Kemudian dengan menggabungkan gerbang Exclusive-OR dengan kombinasi NOT-AND menghasilkan rangkaian pengurangan bilangan biner digital sederhana yang umumnya dikenal sebagai Pengurangan Setengah (Half Subtractor) seperti yang ditunjukkan.
Rangkaian Setengah Pengurang (Half Subtractor)
Setengah pengurang adalah rangkaian logika yang melakukan operasi pengurangan pada dua digit biner. Pengurang setengah menghasilkan jumlah dan bit pinjaman untuk tahap berikutnya.Setengah Pengurang dengan Peminjaman
Dari tabel kebenaran setengah pengurangan kita dapat melihat bahwa output PERBEDAAN ( D ) adalah hasil dari gerbang Exclusive-OR dan Peminjam-out ( Bout ) adalah hasil dari kombinasi NOT-AND. Maka ekspresi Boolean untuk setengah pengurangan adalah sebagai berikut.
Untuk bit PERBEDAAN (Diff):
D = X XOR Y = X ⊕ Y
Untuk bit Peminjam (BORROW)
B = not-X DAN Y = 
.Y
.YJika kita membandingkan ekspresi Boolean dari setengah pengurang dengan setengah penambah, kita dapat melihat bahwa dua ekspresi untuk JUMLAH (penambah) dan PERBEDAAN (pengurang) persis sama dan karena itu seharusnya karena fungsi gerbang Exclusive-OR.
Dua ekspresi Boolean untuk pengurangan bilangan biner PEMINJAM juga sangat mirip dengan yang untuk CARRY adders. Kemudian semua yang diperlukan untuk mengkonversi setengah penambah untuk setengah pengurang adalah inversi dari input minuend X.
Salah satu kelemahan utama dari rangkaian Setengah Pengurangan ketika digunakan sebagai pengurangan bilangan biner, adalah bahwa tidak ada ketentuan untuk "Peminjam-in" dari rangkaian sebelumnya ketika mengurangi beberapa bit data dari satu sama lain.
Maka kita perlu menghasilkan apa yang disebut rangkaian "pengurang biner penuh" untuk memperhitungkan input pinjaman ini dari rangkaian sebelumnya.
Rangkaian Pengurang Biner Penuh
Perbedaan utama antara rangkaian Pengurang Penuh dan Pengurang Setengah sebelumnya adalah bahwa pengurang penuh memiliki tiga input.Dua data bit tunggal input X (minuend) dan Y (subtrahend) sama seperti sebelumnya ditambah input peminjam atau Borrow-in ( B-in ) tambahan untuk menerima pinjaman yang dihasilkan oleh proses pengurangan dari tahap sebelumnya seperti yang ditunjukkan di bawah ini.
Diagram Blok Pengurang Penuh
Kemudian rangkaian kombinasional dari "pengurangan penuh" melakukan operasi pengurangan pada tiga bit biner yang menghasilkan output untuk perbedaan D dan meminjam B-out.
Sama seperti rangkaian penjumlahan bilangan biner, pengurang penuh juga dapat dianggap sebagai dua pengurang setengah terhubung bersama-sama, dengan pengurang paruh pertama meneruskan pinjamannya ke pengurang paruh kedua sebagai berikut.
Diagram Logika Pengurang Penuh
Sebagai rangkaian pengurang penuh atas merupakan dua Setengah Pengurangan mengalir bersama-sama, tabel kebenaran untuk pengurangan penuh akan memiliki delapan kombinasi input yang berbeda karena ada tiga variabel input, data bit dan Borrow-in, BIN input. Juga termasuk perbedaan output, D dan bit Borrow-out, BOUT.
Tabel Kebenaran Pengurang Penuh
Maka ekspresi Boolean untuk pengurangan penuh adalah sebagai berikut.
Untuk bit PERBEDAAN ( D ):
yang dapat disederhanakan juga:
D = (X XOR Y) XOR BIN = (X ⊕ Y) ⊕ BIN
Untuk bit BORROW OUT ( BOUT ):
yang juga akan menyederhanakan:
Pengurangan Bilangan Biner n-bit
Seperti halnya penjumlahan bilangan biner, kita juga dapat memiliki n angka 1 bit pengurang biner penuh yang terhubung atau "mengalir" bersamaan untuk mengurangi dua angka n-bit paralel satu sama lain.Misalnya dua angka biner 4-bit. Kami katakan sebelumnya bahwa satu-satunya perbedaan antara penambah penuh dan pengurang penuh adalah inversi dari salah satu input.
Jadi dengan menggunakan penjumlahan n-bit dan n jumlah inverter ( Gerbang NOT ), proses pengurangan menjadi tambahan karena kita dapat menggunakan notasi komplemen dua pada semua bit dalam subtrahend dan mengatur input carry dari bit yang paling tidak signifikan untuk logika "1" (TINGGI).
Pengurangan Bilangan Biner menggunakan 2 Komplemen
Kemudian kita dapat menggunakan IC full-adder 4-bit seperti 74LS283 dan CD4008 untuk melakukan pengurangan hanya dengan menggunakan komplemen dua pada subtrahend, input B sebagai X - Y sama dengan mengatakan, X + (-Y) yang sama dengan X ditambah komplemen Y untuk keduanya.
Jika kita ingin menggunakan penjumlahan 4-bit sebagai tambahan sekali lagi, yang perlu kita lakukan hanyalah mengatur carry-in ( CIN ) input RENDAH pada logika "0".
Karena kita dapat menggunakan IC penjumlah 4-bit seperti 74LS83 atau 74LS283 sebagai penjumlahan-penuh atau Pengurangan-penuh, mereka tersedia sebagai rangkaian penambah/pengurang tunggal dengan input kontrol tunggal untuk memilih antara dua operasi.