Filter Aktif Variabel - Filter Low, High, Band Pass
Filter Variable adalah jenis multi-feedback rangkaian filter yang dapat menghasilkan ketiga respon filter, Low Pass Filter, High Pass Filter dan Band Pass Filter secara bersamaan dari desain filter aktif tunggal sama.
Filter variable menggunakan tiga (atau lebih) rangkaian Penguat Operasional Op-amp (elemen aktif) yang digabungkan bersama untuk menghasilkan output filter individual tetapi jika diperlukan penguat penjumlahan tambahan juga dapat ditambahkan untuk menghasilkan respon output Notch filter keempat juga.
Filter variabel adalah filter aktif RC orde-2 kedua yang terdiri dari dua Integrator Op-amp yang identik dengan masing-masing bertindak sebagai low pass filter orde-1 pertama, single-pole, penguat penjumlah di sekitar mana kita dapat mengatur gain filter dan feedback (umpan balik) redamannya jaringan.
Sinyal-sinyal output dari ketiga tahap Op-amp dimasukkan kembali ke input yang memungkinkan kita untuk menentukan keadaan rangkaian. Salah satu kelebihan utama dari desain filter variabel adalah bahwa ketiga parameter utama filter, Gain ( A ), frekuensi sudut, ƒC dan filter Q dapat disesuaikan atau diatur secara independen tanpa mempengaruhi kinerja filter.
Sebenarnya jika dirancang dengan benar, frekuensi sudut -3dB, ( ƒc ) untuk respon amplitudo low pass dan respon amplitudo high pass harus identik dengan titik frekuensi tengah dari tahap band pass. Yaitu ƒLP(-3dB) sama dengan ƒHP(-3dB) yang sama dengan ƒBP(tengah). Juga faktor redaman, ( ζ ) untuk respon band pass filter harus sama dengan 1/Q karena Q akan ditetapkan pada -3dB, (0.7071).
Meskipun filter menyediakan output Low Pass Filter (LPF), High Pass Filter (HPF) dan Band Pass Filter (BPF), aplikasi utama dari rangkaian filter jenis ini adalah sebagai desain band pass filter keadaan variabel dengan frekuensi tengah yang ditetapkan oleh dua bilangan bulat RC.
Sementara kita telah melihat sebelumnya bahwa karakteristik band pass filter dapat diperoleh dengan hanya mengalirkan low pass filter dengan high pass filter, filter keadaan band pass variabel memiliki keunggulan yang dapat disesuaikan dengan penawaran yang sangat selektif (Q tinggi) gain tinggi di titik frekuensi pusat/tengah.
Ada beberapa desain filter variabel yang tersedia semua berdasarkan pada desain filter standar dengan variasi inverting dan non-inverting tersedia. Namun, desain filter dasar akan sama untuk kedua variasi seperti yang ditunjukkan pada representasi diagram blok berikut.
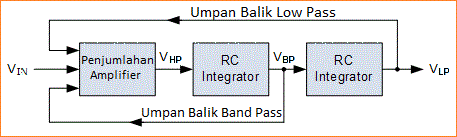
Kemudian kita dapat melihat dari diagram blok dasar di atas bahwa filter variabel memiliki tiga kemungkinan output, VHP, VBP dan VLP dengan masing-masing dari tiga Op-amp. respon notch filter juga dapat diwujudkan dengan penambahan Op-amp keempat.
Dengan tegangan input yang konstan, VIN output dari penguat penjumlah menghasilkan respon high pass yang juga menjadi input dari Integrator RC pertama. Output dari integrator ini menghasilkan respon band pass yang menjadi input dari Integrator RC kedua yang menghasilkan respon low pass pada output-nya. Akibatnya, fungsi transfer yang terpisah untuk masing-masing output sehubungan dengan tegangan input dapat ditemukan.
Karenanya, desain filter variabel non-inverting dasar diberikan sebagai:
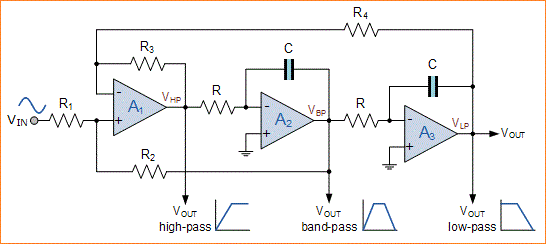
dan respon amplitudo dari tiga output dari filter variabel akan terlihat seperti:

Salah satu elemen desain utama dari filter variabel adalah penggunaan dua integrator Op-amp. Seperti yang kita lihat dalam tutorial Op-amp Integrator, integrator Op-amp menggunakan impedansi tergantung frekuensi dalam bentuk kapasitor dalam loop umpan balik mereka. Sebagai kapasitor digunakan tegangan output sebanding dengan integral dari tegangan input seperti yang ditunjukkan.
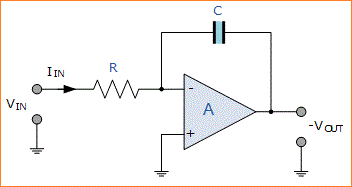
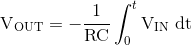
Untuk menyederhanakan matematika, ini juga dapat ditulis ulang dalam domain frekuensi sebagai:

Tegangan output, Vout adalah konstanta 1/RC kali integral dari tegangan input Vin sehubungan dengan waktu. Integrator menghasilkan lag fasa dengan tanda minus ( - ) yang mengindikasikan pergeseran fasa 180° karena sinyal input terhubung langsung ke terminal input inverting/pembalik Op-amp.
Dalam kasus Op-amp A2 di atas, sinyal inputnya terhubung ke output Op-amp yang melanjutkan, A1 sehingga inputnya diberikan sebagai VHP dan outputnya sebagai VBP. Kemudian dari atas, ekspresi untuk Op-amp, A2 dapat ditulis sebagai:
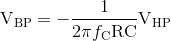
Kemudian dengan mengatur ulang rumus ini kita dapat menemukan fungsi transfer integrator inverting, A2

Asumsi yang sama persis dapat dibuat seperti di atas untuk menemukan fungsi transfer untuk integrator Op-amp lainnya, A3
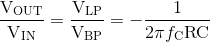
Jadi dua integrator Op-amp, A2 dan A3 terhubung bersama dalam gabungan, sehingga output dari yang pertama ( VBP ) menjadi input yang kedua. Jadi kita dapat melihat bahwa respon band pass dibuat dengan mengintegrasikan respon high pass dan respon low pass dibuat dengan mengintegrasikan respon band pass. Oleh karena itu fungsi transfer antara VHP dan VLP diberikan sebagai:
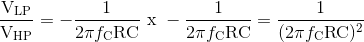
Perhatikan bahwa setiap tahap integrator memberikan output inverting tetapi output yang dijumlahkan akan positif karena mereka membalikkan integrator.
Jika persis nilai yang sama untuk R dan C yang digunakan sehingga dua rangkaian punya waktu integrator yang sama terus-menerus, dua rangkaian penguat dapat dianggap dengan satu rangkaian integrator tunggal yang memiliki frekuensi sudut, ƒC.
Seperti halnya dua rangkaian integrator, filter ini juga memiliki penguat penjumlah diferensial yang memberikan penjumlahan dari inputnya.
Keuntungan atau kelebihannya di sini adalah bahwa input ke penguat penjumlah, A1 menggabungkan umpan balik osilasi, redaman dan sinyal input ke filter karena ketiga output diumpankan kembali ke input penjumlahan.

Penguat operasional Op-amp, A1 terhubung sebagai rangkaian penambahan-pengurangan. Itu adalah jumlah sinyal input, VIN dengan output VBP dari Op-amp A2 dan mengurangi dari itu output VLP dari Op-amp A3, dengan demikian:
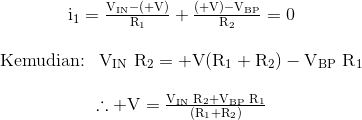
dan
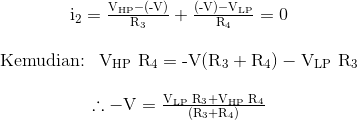
Karena input diferensial, +V dan -V dari penguat operasional Op-amp adalah sama, yaitu: +V - -V, kita dapat mengatur ulang dua ekspresi di atas untuk menemukan fungsi transfer untuk output A1, output high pass.
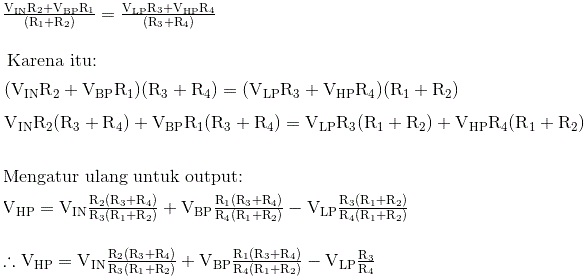
Kita tahu dari atas, bahwa VBP dan VLP adalah output dari dua integrator, A2 dan A3 masing-masing. Dengan mengganti persamaan integrator untuk A2 dan A3 ke dalam persamaan di atas, kita mendapatkan fungsi transfer filter variabel menjadi:

Kami mengatakan sebelumnya bahwa Filter Aktif keadaan Variabel menghasilkan tiga respon filter, Low Pass filter, High Pass filter dan Band Pass filter dan bahwa respon band pass adalah dari filter Q tinggi yang sangat sempit dan ini terbukti dalam fungsi transfer SVF di atas karena menyerupai dari respon orde-2 kedua standar.


Jika kita membuat resistor feedback (umpan balik) R3 dan R4 dengan nilai yang sama, maka frekuensi sudut setiap output dari filter aktif variabel keadaan menjadi:
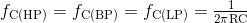
Kemudian tuning variabel keadaan frekuensi sudut dicapai hanya dengan memvariasikan baik tuning Resistor, R atau Kapasitor, C.
Filter variabel keadaan tidak hanya dicirikan oleh respon output individualnya, tetapi juga oleh filter “Q”, Faktor kualitas. Q berkaitan dengan "ketajaman" dari band pass filter kurva respon amplitudo dan semakin tinggi Q, semakin tinggi atau lebih tajam respon output sehingga menghasilkan filter yang sangat selektif.
Untuk band pass filter, Q didefinisikan sebagai frekuensi tengah dibagi dengan filter -3dB bandwidth, yaitu Q = ƒc/BW. Tetapi Q juga dapat ditemukan dari penyebut dari fungsi transfer di atas karena merupakan kebalikan dari faktor redaman ( ζ ). Kemudian Q diberikan sebagai:
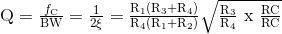
Sekali lagi, jika resistor R3 dan R4 sama dan kedua komponen integrator R dan C sama, maka ekspresi akar kuadrat akhir akan berkurang menjadi: √1 atau hanya 1 karena pembilang dan penyebut membatalkan satu sama lain.
Kami mengatakan di atas bahwa jika resistor, R dan kapasitor umpan balik, C dari dua rangkaian integrator adalah nilai yang sama, yaitu R = R dan C = C, titik frekuensi cut-off atau sudut untuk filter diberikan secara sederhana. sebagai:
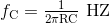
Kita dapat memilih nilai untuk resistor, atau kapasitor untuk menemukan nilai yang lain. Jika kita mengasumsikan nilai 10nF untuk kapasitor yang sesuai maka nilai resistornya adalah:

Memberikan C = 10nF dan R = 15.9kΩ, atau 16kΩ ke nilai pilihan terdekat.
Nilai Q diberikan sebagai 10. Ini berkaitan dengan koefisien redaman filter sebagai:
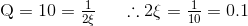
Dalam fungsi transfer variabel di atas, bagian 2ζ diganti oleh kombinasi resistor yang menghasilkan:

Kita tahu dari atas bahwa R = 16kΩ dan C = 10nF, tetapi jika kita mengasumsikan bahwa dua resistor umpan balik, R3 dan R4 adalah sama dan sama dengan 10kΩ, maka persamaan di atas berkurang hingga:

Dengan asumsi nilai yang sesuai untuk resistor input, R1 dari katakan 1kΩ, maka kita dapat menemukan nilai R2 sebagai berikut:
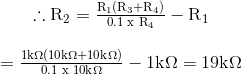
Dari fungsi transfer dinormalisasi di atas, gain band pass DC didefinisikan sebagai Ao dan dari fungsi transfer filter aktif variabel setara ini sama dengan:

Oleh karena itu tegangan gain DC filter dihitung pada 1.9, yang pada dasarnya sama dengan R2/R3. Gain maksimum filter pada ƒC dapat dihitung sebagai: Ao x Q sebagai berikut.
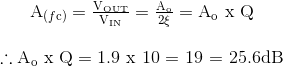
Kita sekarang dapat memplot kurva respon output individu untuk rangkaian filter aktif variabel keadaan pada rentang frekuensi dari 1Hz hingga 1MHz ke Bode Plot seperti yang ditunjukkan.

Kemudian kita dapat melihat dari kurva filter respon atas, bahwa gain DC dari rangkaian filter di 5.57dB yang setara dengan gain tegangan loop terbuka, Ao atau 1.9 yang dihitung di atas.
Respon juga menunjukkan bahwa kurva output puncak pada gain tegangan maksimum 25.6dB pada frekuensi sudut karena nilai Q. Karena Q juga menghubungkan frekuensi pusat band pass filter dengan bandwidthnya, maka bandwidth filter tersebut adalah: ƒo/10 = 100Hz.
Kita telah melihat dalam tutorial filter aktif variabel ini bahwa alih-alih filter aktif yang menghasilkan satu jenis respon frekuensi, kita dapat menggunakan teknik umpan balik berganda untuk menghasilkan ketiga respon filter, Low Pass filter, High Pass filter, dan Pass Band filter secara bersamaan dari satu aktif yang sama desain filter.
Tetapi seperti halnya tiga respon filter dasar, kita dapat menambahkan rangkaian Op-amp tambahan ke desain filter variabel dasar di atas untuk menghasilkan respon output keempat yang menyerupai Notch Filter standar.
Untuk mendapatkan respon notch filter dari desain filter aktif variabel dasar, kita harus menjumlahkan respon output high pass filter dan low pass filter menggunakan penguat penjumlah Op-amp lain, A4 seperti yang ditunjukkan.

Di sini untuk menjaga hal-hal sederhana, kita mengasumsikan bahwa dua resistor input, R5 dan R6 serta resistor umpan balik, R7 semuanya memiliki nilai 10kΩ yang sama dengan R3 dan R4. Oleh karena itu ini menghasilkan filter notch kenaikan 1, unity.
Respon output dari notch filter dan band pass filter terkait dengan frekuensi tengah dari respon band pass sama dengan titik nol respon dari notch filter, dan dalam contoh ini adalah 1kHz.
Bandwidth juga dari notch ditentukan oleh rangkaian Q, persis sama dengan untuk respon band pass. Puncak ke bawah karena itu sama dengan frekuensi pusat dibagi dengan bandwidth -3dB, yaitu perbedaan frekuensi antara titik -3dB di kedua sisi notch. Perhatikan bahwa faktor kualitas Q tidak ada hubungannya dengan kedalaman notch yang sebenarnya.
Desain notch filter dasar ini (stop-band) hanya memiliki dua input yang diterapkan pada penguat penjumlahannya, output low pass, VLP dan output high pass, VHP. Namun, ada dua sinyal lagi yang tersedia untuk kita gunakan dari rangkaian filter variabel dasar, output jalur pita, VBP dan sinyal input itu sendiri, VIN.
Jika salah satu dari dua sinyal ini juga digunakan sebagai input ke penguat penjumlah notch filter beserta sinyal low pass filter dan high pass filter, maka kedalaman notch dapat dikontrol. Bergantung pada bagaimana Anda ingin mengontrol output dari bagian notch filter akan bergantung pada salah satu dari dua sinyal yang tersedia yang akan Anda gunakan.
Jika disyaratkan bahwa notch output berubah dari respon negatif ke respon positif pada frekuensi alami yang tidak teredam ƒo maka sinyal band pass output VBP akan digunakan. Demikian juga, jika diperlukan bahwa notch output hanya bervariasi pada kedalaman negatif ke bawah, maka sinyal input, VIN akan digunakan.
Jika salah satu dari dua sinyal tambahan ini terhubung ke Op-amp penjumlah (Summing) melalui resistor variabel, maka kedalaman dan arah notch dapat dikontrol sepenuhnya. Pertimbangkan rangkaian notch filter yang dimodifikasi di bawah ini.
Keuntungan/kelebihan dari filter variabel dibandingkan desain filter dasar lainnya adalah bahwa tiga parameter filter utama, Gain, Q dan ƒc dapat disesuaikan secara independen.
Kami juga telah melihat di sini bahwa filter juga mudah disetel karena frekuensi sudut, ƒc dapat diatur dan disesuaikan dengan memvariasikan baik R atau C tanpa mempengaruhi faktor redaman filter.
Namun, pada frekuensi sudut yang lebih tinggi dan faktor redaman yang lebih besar, filter dapat menjadi tidak stabil sehingga paling baik digunakan dengan Q rendah, kurang dari 10, dan pada frekuensi sudut rendah.
Desain filter aktif variabel dasar menggunakan tiga bagian Op-amp untuk menghasilkan outputnya, tetapi kita juga telah melihat bahwa dengan penambahan bagian Op-amp keempat yang merangkum bagian low pass dan high pass secara bersamaan, notch (band-stop) respon output filter juga dapat dicapai pada frekuensi pusat yang diinginkan.
Filter variable menggunakan tiga (atau lebih) rangkaian Penguat Operasional Op-amp (elemen aktif) yang digabungkan bersama untuk menghasilkan output filter individual tetapi jika diperlukan penguat penjumlahan tambahan juga dapat ditambahkan untuk menghasilkan respon output Notch filter keempat juga.
Filter variabel adalah filter aktif RC orde-2 kedua yang terdiri dari dua Integrator Op-amp yang identik dengan masing-masing bertindak sebagai low pass filter orde-1 pertama, single-pole, penguat penjumlah di sekitar mana kita dapat mengatur gain filter dan feedback (umpan balik) redamannya jaringan.
Sinyal-sinyal output dari ketiga tahap Op-amp dimasukkan kembali ke input yang memungkinkan kita untuk menentukan keadaan rangkaian. Salah satu kelebihan utama dari desain filter variabel adalah bahwa ketiga parameter utama filter, Gain ( A ), frekuensi sudut, ƒC dan filter Q dapat disesuaikan atau diatur secara independen tanpa mempengaruhi kinerja filter.
Sebenarnya jika dirancang dengan benar, frekuensi sudut -3dB, ( ƒc ) untuk respon amplitudo low pass dan respon amplitudo high pass harus identik dengan titik frekuensi tengah dari tahap band pass. Yaitu ƒLP(-3dB) sama dengan ƒHP(-3dB) yang sama dengan ƒBP(tengah). Juga faktor redaman, ( ζ ) untuk respon band pass filter harus sama dengan 1/Q karena Q akan ditetapkan pada -3dB, (0.7071).
Meskipun filter menyediakan output Low Pass Filter (LPF), High Pass Filter (HPF) dan Band Pass Filter (BPF), aplikasi utama dari rangkaian filter jenis ini adalah sebagai desain band pass filter keadaan variabel dengan frekuensi tengah yang ditetapkan oleh dua bilangan bulat RC.
Sementara kita telah melihat sebelumnya bahwa karakteristik band pass filter dapat diperoleh dengan hanya mengalirkan low pass filter dengan high pass filter, filter keadaan band pass variabel memiliki keunggulan yang dapat disesuaikan dengan penawaran yang sangat selektif (Q tinggi) gain tinggi di titik frekuensi pusat/tengah.
Ada beberapa desain filter variabel yang tersedia semua berdasarkan pada desain filter standar dengan variasi inverting dan non-inverting tersedia. Namun, desain filter dasar akan sama untuk kedua variasi seperti yang ditunjukkan pada representasi diagram blok berikut.
Diagram Blok Filter Keadaan Variabel

Kemudian kita dapat melihat dari diagram blok dasar di atas bahwa filter variabel memiliki tiga kemungkinan output, VHP, VBP dan VLP dengan masing-masing dari tiga Op-amp. respon notch filter juga dapat diwujudkan dengan penambahan Op-amp keempat.
Dengan tegangan input yang konstan, VIN output dari penguat penjumlah menghasilkan respon high pass yang juga menjadi input dari Integrator RC pertama. Output dari integrator ini menghasilkan respon band pass yang menjadi input dari Integrator RC kedua yang menghasilkan respon low pass pada output-nya. Akibatnya, fungsi transfer yang terpisah untuk masing-masing output sehubungan dengan tegangan input dapat ditemukan.
Karenanya, desain filter variabel non-inverting dasar diberikan sebagai:
Rangkaian Filter Aktif Keadaan Variabel

dan respon amplitudo dari tiga output dari filter variabel akan terlihat seperti:
Respon Normalisasi dari Filter Aktif Keadaan Variabel

Salah satu elemen desain utama dari filter variabel adalah penggunaan dua integrator Op-amp. Seperti yang kita lihat dalam tutorial Op-amp Integrator, integrator Op-amp menggunakan impedansi tergantung frekuensi dalam bentuk kapasitor dalam loop umpan balik mereka. Sebagai kapasitor digunakan tegangan output sebanding dengan integral dari tegangan input seperti yang ditunjukkan.
Rangkaian Integrator Op-amp

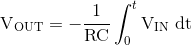
Untuk menyederhanakan matematika, ini juga dapat ditulis ulang dalam domain frekuensi sebagai:

Tegangan output, Vout adalah konstanta 1/RC kali integral dari tegangan input Vin sehubungan dengan waktu. Integrator menghasilkan lag fasa dengan tanda minus ( - ) yang mengindikasikan pergeseran fasa 180° karena sinyal input terhubung langsung ke terminal input inverting/pembalik Op-amp.
Dalam kasus Op-amp A2 di atas, sinyal inputnya terhubung ke output Op-amp yang melanjutkan, A1 sehingga inputnya diberikan sebagai VHP dan outputnya sebagai VBP. Kemudian dari atas, ekspresi untuk Op-amp, A2 dapat ditulis sebagai:
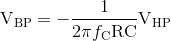
Kemudian dengan mengatur ulang rumus ini kita dapat menemukan fungsi transfer integrator inverting, A2
Fungsi Transfer Op-amp A2

Asumsi yang sama persis dapat dibuat seperti di atas untuk menemukan fungsi transfer untuk integrator Op-amp lainnya, A3
Fungsi Transfer Op-amp A3
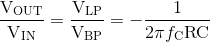
Jadi dua integrator Op-amp, A2 dan A3 terhubung bersama dalam gabungan, sehingga output dari yang pertama ( VBP ) menjadi input yang kedua. Jadi kita dapat melihat bahwa respon band pass dibuat dengan mengintegrasikan respon high pass dan respon low pass dibuat dengan mengintegrasikan respon band pass. Oleh karena itu fungsi transfer antara VHP dan VLP diberikan sebagai:
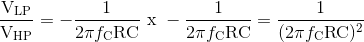
Perhatikan bahwa setiap tahap integrator memberikan output inverting tetapi output yang dijumlahkan akan positif karena mereka membalikkan integrator.
Jika persis nilai yang sama untuk R dan C yang digunakan sehingga dua rangkaian punya waktu integrator yang sama terus-menerus, dua rangkaian penguat dapat dianggap dengan satu rangkaian integrator tunggal yang memiliki frekuensi sudut, ƒC.
Seperti halnya dua rangkaian integrator, filter ini juga memiliki penguat penjumlah diferensial yang memberikan penjumlahan dari inputnya.
Keuntungan atau kelebihannya di sini adalah bahwa input ke penguat penjumlah, A1 menggabungkan umpan balik osilasi, redaman dan sinyal input ke filter karena ketiga output diumpankan kembali ke input penjumlahan.
Rangkaian Penjumlahan Penguat Operasional Op-amp

Penguat operasional Op-amp, A1 terhubung sebagai rangkaian penambahan-pengurangan. Itu adalah jumlah sinyal input, VIN dengan output VBP dari Op-amp A2 dan mengurangi dari itu output VLP dari Op-amp A3, dengan demikian:
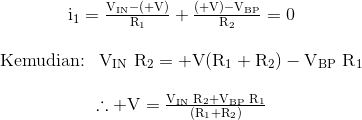
dan
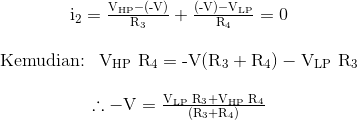
Karena input diferensial, +V dan -V dari penguat operasional Op-amp adalah sama, yaitu: +V - -V, kita dapat mengatur ulang dua ekspresi di atas untuk menemukan fungsi transfer untuk output A1, output high pass.
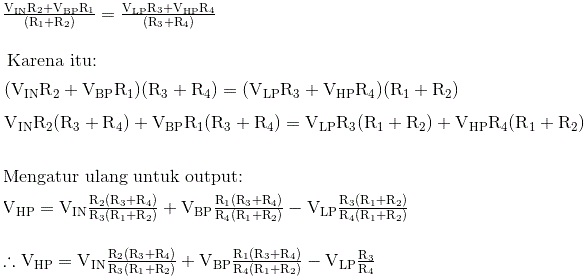
Kita tahu dari atas, bahwa VBP dan VLP adalah output dari dua integrator, A2 dan A3 masing-masing. Dengan mengganti persamaan integrator untuk A2 dan A3 ke dalam persamaan di atas, kita mendapatkan fungsi transfer filter variabel menjadi:
Fungsi Transfer Filter Aktif Variabel

Kami mengatakan sebelumnya bahwa Filter Aktif keadaan Variabel menghasilkan tiga respon filter, Low Pass filter, High Pass filter dan Band Pass filter dan bahwa respon band pass adalah dari filter Q tinggi yang sangat sempit dan ini terbukti dalam fungsi transfer SVF di atas karena menyerupai dari respon orde-2 kedua standar.
Fungsi Transfer Orde-2 kedua yang Di-Normalisasi

Frekuensi Sudut Filter, ƒC
Jika kita membuat resistor input integrator dan kapasitor umpan balik sama, maka frekuensi sudut filter variabel dapat dengan mudah disetel tanpa mempengaruhi keseluruhan Q -nya. Demikian juga, nilai Q dapat bervariasi tanpa mengubah frekuensi sudut. Kemudian frekuensi sudut diberikan sebagai:Frekuensi Filter Aktif Variabel

Jika kita membuat resistor feedback (umpan balik) R3 dan R4 dengan nilai yang sama, maka frekuensi sudut setiap output dari filter aktif variabel keadaan menjadi:
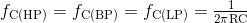
Kemudian tuning variabel keadaan frekuensi sudut dicapai hanya dengan memvariasikan baik tuning Resistor, R atau Kapasitor, C.
Filter variabel keadaan tidak hanya dicirikan oleh respon output individualnya, tetapi juga oleh filter “Q”, Faktor kualitas. Q berkaitan dengan "ketajaman" dari band pass filter kurva respon amplitudo dan semakin tinggi Q, semakin tinggi atau lebih tajam respon output sehingga menghasilkan filter yang sangat selektif.
Untuk band pass filter, Q didefinisikan sebagai frekuensi tengah dibagi dengan filter -3dB bandwidth, yaitu Q = ƒc/BW. Tetapi Q juga dapat ditemukan dari penyebut dari fungsi transfer di atas karena merupakan kebalikan dari faktor redaman ( ζ ). Kemudian Q diberikan sebagai:
Faktor Q dari Filter Aktif keadaan Variabel
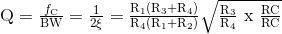
Sekali lagi, jika resistor R3 dan R4 sama dan kedua komponen integrator R dan C sama, maka ekspresi akar kuadrat akhir akan berkurang menjadi: √1 atau hanya 1 karena pembilang dan penyebut membatalkan satu sama lain.
Contoh: Filter Aktif Variabel No.1
Rancang Filter Aktif keadaan Variabel yang memiliki frekuensi sudut (tidak terbebani alami), ƒC dari 1kHz dan faktor kualitas, Q dari 10. Asumsikan resistor dan kapasitor penentu frekuensi sama. Tentukan filter gain DC dan gambar rangkaian yang dihasilkan dan Bode plot.Kami mengatakan di atas bahwa jika resistor, R dan kapasitor umpan balik, C dari dua rangkaian integrator adalah nilai yang sama, yaitu R = R dan C = C, titik frekuensi cut-off atau sudut untuk filter diberikan secara sederhana. sebagai:
Frekuensi Sudut Filter
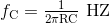
Kita dapat memilih nilai untuk resistor, atau kapasitor untuk menemukan nilai yang lain. Jika kita mengasumsikan nilai 10nF untuk kapasitor yang sesuai maka nilai resistornya adalah:

Memberikan C = 10nF dan R = 15.9kΩ, atau 16kΩ ke nilai pilihan terdekat.
Nilai Q diberikan sebagai 10. Ini berkaitan dengan koefisien redaman filter sebagai:
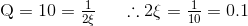
Dalam fungsi transfer variabel di atas, bagian 2ζ diganti oleh kombinasi resistor yang menghasilkan:

Kita tahu dari atas bahwa R = 16kΩ dan C = 10nF, tetapi jika kita mengasumsikan bahwa dua resistor umpan balik, R3 dan R4 adalah sama dan sama dengan 10kΩ, maka persamaan di atas berkurang hingga:

Dengan asumsi nilai yang sesuai untuk resistor input, R1 dari katakan 1kΩ, maka kita dapat menemukan nilai R2 sebagai berikut:
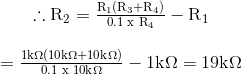
Dari fungsi transfer dinormalisasi di atas, gain band pass DC didefinisikan sebagai Ao dan dari fungsi transfer filter aktif variabel setara ini sama dengan:
Filter Aktif Variabel Band Pass Gain DC

Oleh karena itu tegangan gain DC filter dihitung pada 1.9, yang pada dasarnya sama dengan R2/R3. Gain maksimum filter pada ƒC dapat dihitung sebagai: Ao x Q sebagai berikut.
Filter Aktif Variabel Gain Maksimum
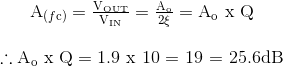
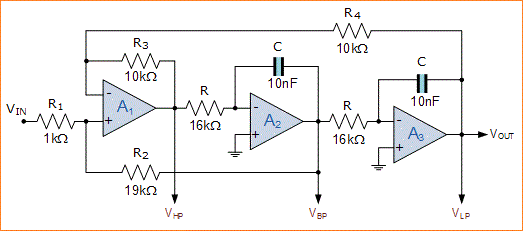
Rangkaian Filter Aktif Variabel keadaan
Maka desain rangkaian filter variabel akan menjadi: R = 16kΩ, C = 10nF, R1 = 1kΩ, R2 = 19kΩ dan R3 = R4 = 10kΩ seperti yang ditunjukkan.Desain Rangkaian Filter Aktif Variabel keadaan

Kita sekarang dapat memplot kurva respon output individu untuk rangkaian filter aktif variabel keadaan pada rentang frekuensi dari 1Hz hingga 1MHz ke Bode Plot seperti yang ditunjukkan.
Bode Plot Filter Aktif Variabel

Kemudian kita dapat melihat dari kurva filter respon atas, bahwa gain DC dari rangkaian filter di 5.57dB yang setara dengan gain tegangan loop terbuka, Ao atau 1.9 yang dihitung di atas.
Respon juga menunjukkan bahwa kurva output puncak pada gain tegangan maksimum 25.6dB pada frekuensi sudut karena nilai Q. Karena Q juga menghubungkan frekuensi pusat band pass filter dengan bandwidthnya, maka bandwidth filter tersebut adalah: ƒo/10 = 100Hz.
Kita telah melihat dalam tutorial filter aktif variabel ini bahwa alih-alih filter aktif yang menghasilkan satu jenis respon frekuensi, kita dapat menggunakan teknik umpan balik berganda untuk menghasilkan ketiga respon filter, Low Pass filter, High Pass filter, dan Pass Band filter secara bersamaan dari satu aktif yang sama desain filter.
Tetapi seperti halnya tiga respon filter dasar, kita dapat menambahkan rangkaian Op-amp tambahan ke desain filter variabel dasar di atas untuk menghasilkan respon output keempat yang menyerupai Notch Filter standar.
Desain Notch Filter
Sebuah penyaring Notch Filter pada dasarnya adalah kebalikan dari band pass filter, dalam hal ini menolak atau berhenti pada frekuensi band tertentu. Kemudian filter notch juga dikenal sebagai "Band Stop Filter".Untuk mendapatkan respon notch filter dari desain filter aktif variabel dasar, kita harus menjumlahkan respon output high pass filter dan low pass filter menggunakan penguat penjumlah Op-amp lain, A4 seperti yang ditunjukkan.
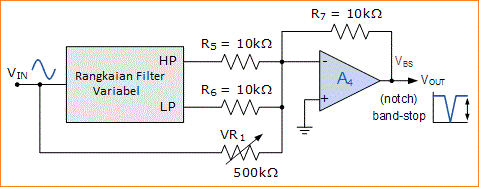
Rangkaian Notch Filter

Di sini untuk menjaga hal-hal sederhana, kita mengasumsikan bahwa dua resistor input, R5 dan R6 serta resistor umpan balik, R7 semuanya memiliki nilai 10kΩ yang sama dengan R3 dan R4. Oleh karena itu ini menghasilkan filter notch kenaikan 1, unity.
Respon output dari notch filter dan band pass filter terkait dengan frekuensi tengah dari respon band pass sama dengan titik nol respon dari notch filter, dan dalam contoh ini adalah 1kHz.
Bandwidth juga dari notch ditentukan oleh rangkaian Q, persis sama dengan untuk respon band pass. Puncak ke bawah karena itu sama dengan frekuensi pusat dibagi dengan bandwidth -3dB, yaitu perbedaan frekuensi antara titik -3dB di kedua sisi notch. Perhatikan bahwa faktor kualitas Q tidak ada hubungannya dengan kedalaman notch yang sebenarnya.
Desain notch filter dasar ini (stop-band) hanya memiliki dua input yang diterapkan pada penguat penjumlahannya, output low pass, VLP dan output high pass, VHP. Namun, ada dua sinyal lagi yang tersedia untuk kita gunakan dari rangkaian filter variabel dasar, output jalur pita, VBP dan sinyal input itu sendiri, VIN.
Jika salah satu dari dua sinyal ini juga digunakan sebagai input ke penguat penjumlah notch filter beserta sinyal low pass filter dan high pass filter, maka kedalaman notch dapat dikontrol. Bergantung pada bagaimana Anda ingin mengontrol output dari bagian notch filter akan bergantung pada salah satu dari dua sinyal yang tersedia yang akan Anda gunakan.
Jika disyaratkan bahwa notch output berubah dari respon negatif ke respon positif pada frekuensi alami yang tidak teredam ƒo maka sinyal band pass output VBP akan digunakan. Demikian juga, jika diperlukan bahwa notch output hanya bervariasi pada kedalaman negatif ke bawah, maka sinyal input, VIN akan digunakan.
Jika salah satu dari dua sinyal tambahan ini terhubung ke Op-amp penjumlah (Summing) melalui resistor variabel, maka kedalaman dan arah notch dapat dikontrol sepenuhnya. Pertimbangkan rangkaian notch filter yang dimodifikasi di bawah ini.
Kedalaman Notch Filter Variabel

Ringkasan Filter Aktif KeadaanVariabel
Rangkaian State Variable Filter, ( SVF ) adalah desain filter RC aktif orde-2 kedua yang menggunakan beberapa teknik umpan balik (feedback) untuk menghasilkan tiga output respon frekuensi yang berbeda, yaitu: Low Pass, High Pass, dan Band Pass dari filter tunggal yang sama.Keuntungan/kelebihan dari filter variabel dibandingkan desain filter dasar lainnya adalah bahwa tiga parameter filter utama, Gain, Q dan ƒc dapat disesuaikan secara independen.
Kami juga telah melihat di sini bahwa filter juga mudah disetel karena frekuensi sudut, ƒc dapat diatur dan disesuaikan dengan memvariasikan baik R atau C tanpa mempengaruhi faktor redaman filter.
Namun, pada frekuensi sudut yang lebih tinggi dan faktor redaman yang lebih besar, filter dapat menjadi tidak stabil sehingga paling baik digunakan dengan Q rendah, kurang dari 10, dan pada frekuensi sudut rendah.
Desain filter aktif variabel dasar menggunakan tiga bagian Op-amp untuk menghasilkan outputnya, tetapi kita juga telah melihat bahwa dengan penambahan bagian Op-amp keempat yang merangkum bagian low pass dan high pass secara bersamaan, notch (band-stop) respon output filter juga dapat dicapai pada frekuensi pusat yang diinginkan.