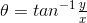Bilangan Kompleks dan Fasor

Matematika yang digunakan dalam Teknik Elektro untuk menghitung resistansi, arus, atau tegangan DC menggunakan apa yang disebut "bilangan real" yang digunakan sebagai bilangan bulat atau sebagai pecahan. Tetapi bilangan real bukan satu-satunya jenis angka yang perlu kita gunakan terutama ketika berhadapan dengan sumber dan vektor sinusoidal yang bergantung pada frekuensi.

Selain menggunakan bilangan real atau nyata, Bilangan Kompleks diperkenalkan untuk memungkinkan persamaan kompleks diselesaikan dengan bilangan yang merupakan akar kuadrat dari bilangan negatif, √-1.

Dalam teknik kelistrikan, jenis angka ini disebut "angka imajiner" dan untuk membedakan angka imajiner dari angka asli, huruf "j" yang biasa dikenal dalam teknik listrik sebagai operator-j, digunakan. Dengan demikian huruf "j" ditempatkan di depan bilangan real untuk menandakan operasi bilangan imajinernya.

Contoh bilangan imajiner adalah: j3, j12, j100 dll. Kemudian bilangan kompleks terdiri dari dua bagian yang berbeda tetapi sangat terkait, "Bilangan Nyata" ditambah "Bilangan Imajiner".

Bilangan Kompleks mewakili titik dalam kompleks dua dimensi atau bidang-s yang dirujuk ke dua sumbu berbeda. Sumbu horizontal disebut "sumbu nyata" sedangkan sumbu vertikal disebut "sumbu imajiner". Bagian nyata dan imajiner dari bilangan kompleks disingkat masing-masing sebagai Re(z) dan Im(z).

Bilangan kompleks yang terdiri dari bilangan real (komponen aktif) dan imajiner (komponen reaktif) dapat ditambahkan, dikurangi dan digunakan dengan cara yang persis sama seperti aljabar dasar digunakan untuk menganalisis Rangkaian DC.

Aturan dan hukum yang digunakan dalam matematika untuk penambahan atau pengurangan bilangan imajiner sama dengan bilangan real, j2 + j4 = j6 dll. Satu-satunya perbedaan adalah dalam penggandaan karena dua bilangan imajiner dikalikan bersama menjadi bilangan real negatif. Bilangan real juga dapat dianggap sebagai bilangan kompleks tetapi dengan bagian imajiner nol berlabel j0.

j-operator memiliki nilai persis sama dengan √-1, perkalian sehingga berturut-turut “ j “, (j x j) akan menghasilkan j memiliki nilai-nilai berikut, -1, j dan 1. Sebagai j-operator yang umumnya digunakan untuk menunjukkan rotasi berlawanan arah jarum jam dari vektor, masing-masing perkalian berturut-turut atau kekuatan “ j “, j², j³ dll, akan memaksa vektor untuk memutar melalui sudut tetap 90° dalam berlawanan arah jarum jam arah seperti yang ditunjukkan di bawah ini.

Demikian juga, jika perkalian vektor menghasilkan -j operator maka pergeseran fasa akan -90°, yaitu rotasi searah jarum jam.

Rotasi Vektor Operator-j

Jadi dengan mengalikan angka imajiner dengan j² akan memutar vektor sebesar 180° berlawanan arah jarum jam, mengalikannya dengan j³ memutarnya 270° dan dengan j⁴ memutarnya 360° atau kembali ke posisi semula. Perkalian dengan j¹⁰ atau j³⁰ akan menyebabkan vektor berputar berlawanan arah jarum jam dengan jumlah yang sesuai. Di setiap rotasi berturut-turut, besarnya vektor selalu tetap sama.

Dalam Teknik Elektro ada beberapa cara berbeda untuk merepresentasikan bilangan kompleks baik secara grafis maupun matematis. Salah satu cara yang menggunakan aturan cosinus dan sinus disebut Cartesian atau Rectangular.

Bilangan Kompleks menggunakan Bentuk Rectangular

Dalam tutorial terakhir tentang Fasor, kami melihat bahwa bilangan kompleks diwakili oleh bagian nyata dan bagian imajiner yang mengambil bentuk umum dari: Z = x +jy

Dimana:
  Z   - adalah Nomor Kompleks yang mewakili Vektor
  x   - adalah bagian Nyata atau komponen Aktif
  y   - adalah bagian Imajiner atau komponen Reaktif
  j   - didefinisikan oleh √-1

Dalam bentuk persegi panjang (rectangular), bilangan kompleks dapat direpresentasikan sebagai titik pada bidang dua dimensi yang disebut kompleks atau bidang-s (s-plane). Jadi misalnya, Z = 6 + j4 mewakili satu titik yang koordinatnya mewakili 6 pada sumbu real horisontal dan 4 pada sumbu imajiner vertikal seperti yang ditunjukkan.

Bilangan Kompleks menggunakan Kompleks atau s-plane

Tetapi karena bagian nyata dan imajiner dari bilangan kompleks dalam bentuk persegi panjang dapat berupa bilangan positif atau bilangan negatif, maka sumbu nyata dan imajiner juga harus diperluas dalam arah positif dan negatif. Ini kemudian menghasilkan bidang kompleks dengan empat kuadran yang disebut Diagram Argand seperti yang ditunjukkan di bawah ini.

Diagram Argand Empat Kuadran

Pada diagram Argand, sumbu horizontal mewakili semua bilangan real positif di sebelah kanan sumbu imajiner vertikal dan semua bilangan real negatif di sebelah kiri sumbu imajiner vertikal.

Semua bilangan imajiner positif diwakili di atas sumbu horizontal sementara semua angka imajiner negatif berada di bawah sumbu nyata horisontal. Ini kemudian menghasilkan bidang kompleks dua dimensi dengan empat kuadran yang berlabel, QI, QII, QIII, dan QIV.

Diagram Argand di atas juga dapat digunakan untuk mewakili fasor berputar sebagai titik di bidang kompleks yang jari-jarinya diberikan oleh besarnya fasor akan menggambar lingkaran penuh di sekitarnya untuk setiap 2π/ω detik. Kemudian kita dapat memperpanjang rumus ini lebih lanjut untuk menunjukkan definisi dari sejumlah kompleks dalam kedua bentuk polar dan segi empat untuk rotasi 90°.

0° = ±360° = +1 = 1∠0° = 1+j0
+90° = +√-1 = +j = 1∠+90° = 0+j1
-90° = -√-1 = -j = 1∠-90° = 0-j1
±180° = (√-1)² = -1 = 1∠±180° = -1+j0

Bilangan Kompleks juga dapat memiliki bagian "nol" nyata atau imajiner seperti: Z = 6 + j0 atau Z = 0 + j4. Dalam hal ini titik diplot langsung ke sumbu nyata atau imajiner.

Juga, sudut bilangan kompleks dapat dihitung menggunakan trigonometri sederhana untuk menghitung sudut segitiga siku-siku, atau diukur berlawanan arah jarum jam di sekitar diagram Argand mulai dari sumbu nyata positif.

Maka sudut antara 0 dan 90° akan berada di kuadran pertama (I), sudut (θ) antara 90 dan 180° di kuadran kedua (II). Kuadran ketiga (III) termasuk sudut antara 180 dan 270° sedangkan kuadran keempat dan terakhir (IV) yang melengkapi lingkaran penuh, termasuk sudut antara 270 dan 360° dan seterusnya. Di keempat kuadran sudut yang relevan dapat ditemukan dari:

tan^-1(komponen imajiner ÷ komponen nyata)

Penambahan dan Pengurangan Bilangan Kompleks

Penambahan atau pengurangan bilangan kompleks dapat dilakukan baik secara matematis atau grafis dalam bentuk persegi panjang. Sebagai tambahan, bagian nyata pertama-tama ditambahkan bersama-sama untuk membentuk bagian nyata dari jumlah, dan kemudian bagian imajiner untuk membentuk bagian imajiner dari jumlah dan proses ini adalah sebagai berikut menggunakan dua bilangan kompleks A dan B sebagai contoh.

Penambahan dan Pengurangan Kompleks

A = x+jy   B = w + jz
A + B = (x + w) + j(y + z)
A - B = (x - w) + j(y - z)

Contoh: Bilangan Kompleks No.1

Dua vektor didefinisikan sebagai, A = 4 + j1 dan B = 2 + j3 masing-masing. Tentukan jumlah dan perbedaan dari kedua vektor dalam bentuk persegi panjang (a + jb) dan secara grafis sebagai Diagram Argand.

Penambahan dan Pengurangan bentuk Matematika

Penambahan vektor
A + B = (4+j1) + (2+j3)
A + B = (4+2) + j(1+3) = 6+j4

Pengurangan vektor

A - B = (4+j1) - (2+j3)
A + B = (4-2) + j(1-3) = 2-j2

Penambahan dan Pengurangan bentuk Grafik

Perkalian dan Pembagian Angka Kompleks

Penggandaan bilangan kompleks dalam bentuk persegi panjang mengikuti kurang lebih aturan yang sama seperti untuk aljabar normal bersama dengan beberapa aturan tambahan untuk perkalian berturut-turut dari operator-j di mana: j² = -1. Jadi misalnya, mengalikan dua vektor kita dari atas A = 4 + j1 dan B = 2 + j3 akan memberi kita hasil berikut.

A x B = (4+j1) (2+j3)

  =8 + j12 + j2 + j²3

Akan tetapi,
j² = -1,
  = 8 + j14 - 3
A x B = 5  + j14

Secara matematis, pembagian bilangan kompleks dalam bentuk persegi panjang sedikit lebih sulit untuk dilakukan karena memerlukan penggunaan fungsi konjugasi penyebut untuk mengubah penyebut persamaan menjadi bilangan real. Ini disebut "rasionalisasi". Kemudian pembagian bilangan kompleks paling baik dilakukan dengan menggunakan "Bentuk Kutub", yang akan kita lihat nanti. Namun, sebagai contoh dalam bentuk persegi panjang memungkinkan menemukan nilai vektor A dibagi dengan vektor B .

Konjugasi Kompleks

Konjugasi kompleks, atau hanya Conjugate dari bilangan kompleks ditemukan oleh membalikkan tanda aljabar bilangan kompleks angka imajiner hanya sambil menjaga tanda aljabar dari jumlah sebenarnya yang sama dan untuk mengidentifikasi konjugat kompleks z simbol 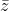 digunakan.

Sebagai contoh, konjugat z = 6 + j4 adalah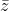  = 6 - j4 , demikian juga konjugat z = 6 - j4 adalah  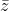= 6 + j4.

Titik-titik pada diagram Argand untuk konjugat kompleks memiliki posisi horizontal yang sama pada sumbu nyata dengan bilangan kompleks asli, tetapi berlawanan posisi vertikal. Dengan demikian, konjugat kompleks dapat dianggap sebagai cerminan bilangan kompleks. Contoh berikut menunjukkan bilangan kompleks, 6 + j4 dan konjugatnya dalam bidang kompleks.

Konjugasi Bilangan Kompleks

Jumlah bilangan kompleks dan konjugat kompleksnya akan selalu menjadi bilangan real seperti yang telah kita lihat di atas. Kemudian penambahan bilangan kompleks dan konjugatnya memberikan hasil sebagai bilangan real atau komponen aktif saja, sedangkan pengurangannya memberikan bilangan imajiner atau komponen reaktif saja. Konjugasi bilangan kompleks adalah elemen penting yang digunakan dalam Teknik Elektro untuk menentukan daya nyata dari rangkaian AC menggunakan bentuk persegi panjang.

Bilangan Kompleks menggunakan Bentuk Kutub (polar)

Tidak seperti bentuk persegi panjang yang memplot poin dalam bidang kompleks, Bentuk Polar dari bilangan kompleks ditulis dalam hal besarnya dan sudutnya.

Dengan demikian, vektor bentuk polar disajikan sebagai: Z = A ∠ ± θ,

di mana:
Z adalah bilangan kompleks dalam bentuk polar,
A adalah besarnya atau modulo vektor dan
θ adalah sudut atau argumen A yang dapat berupa positif atau negatif.

Besar dan sudut titik masih tetap sama dengan untuk bentuk persegi panjang di atas, kali ini dalam bentuk kutub lokasi titik diwakili dalam "bentuk segitiga" seperti yang ditunjukkan di bawah ini.

Representasi Bentuk Kutub dari bilangan Kompleks

Karena representasi kutub dari suatu titik didasarkan pada bentuk segitiga, kita dapat menggunakan geometri sederhana dari segitiga dan khususnya trigonometri dan Teorema Pythagoras pada segitiga untuk menemukan besarnya dan sudut bilangan kompleks. Seperti yang kita ingat dari sekolah, trigonometri membahas hubungan antara sisi dan sudut segitiga sehingga kita dapat menggambarkan hubungan antara sisi sebagai:

Dengan menggunakan trigonometri lagi, sudut θ dari A diberikan sebagai berikut.

Kemudian dalam bentuk Kutub panjang A dan sudutnya mewakili bilangan kompleks, bukan titik. Juga dalam bentuk kutub, konjugat dari bilangan kompleks memiliki besaran atau modulus yang sama dengan tanda sudut yang berubah, jadi misalnya konjugat 6 ∠30° akan menjadi 6 ∠–30°.

Konversi antara Bentuk Persegi Panjang dan Bentuk Kutub

Dalam bentuk persegi panjang kita dapat mengekspresikan vektor dalam hal koordinat persegi panjangnya, dengan sumbu horizontal menjadi sumbu nyata dan sumbu vertikal menjadi sumbu imajiner atau komponen-j. Dalam bentuk kutub, sumbu nyata dan imajiner ini hanya diwakili oleh " A ∠θ ". Kemudian menggunakan contoh kami di atas, hubungan antara bentuk persegi panjang dan bentuk kutub dapat didefinisikan sebagai.

Mengubah Bentuk Kutub menjadi Bentuk Persegi Panjang, (P → R)

6 ∠30° = x+jy

Namun,
x = A.cosθ   y=A.sinθ

Oleh karena itu,
6 ∠30° = (6 cosθ) + j(6sinθ)
= (6 cos30°) + j(6sin30°)
= (6x0.866) + j(6x0.5)
= 5.2 + j3

Kami juga dapat mengkonversi kembali dari bentuk persegi panjang ke bentuk kutub sebagai berikut.

Mengubah Bentuk Persegi Panjang menjadi Bentuk Kutub, (R → P)

Perkalian dan Pembagian Bentuk Kutub (polar)

Bentuk persegi panjang adalah yang terbaik untuk menambah dan mengurangi bilangan kompleks seperti yang kita lihat di atas, tetapi bentuk kutub seringkali lebih baik untuk mengalikan dan membagi. Untuk mengalikan dua vektor dalam bentuk polar, pertama-tama kita harus mengalikan dua modulus atau besaran dan kemudian menambahkan sudut-sudutnya.

Perkalian dalam Bentuk Kutub

Z₁ x Z₂ = A₁ x A₂ ∠θ₁ + θ₂

Mengalikan bersama-sama menjadi 6 ∠30° dan 8 ∠- 45° dalam bentuk kutub.

Z₁ x Z₂ = 6 x 8 ∠30° + (-45°) = 48 ∠-15°

Pembagian dalam Bentuk Kutub

Demikian juga, untuk membagi dua vektor dalam bentuk kutub, kita harus membagi dua modulus dan kemudian kurangi sudutnya seperti yang ditunjukkan.

Untungnya kalkulator ilmiah modern saat ini telah membangun fungsi matematika (periksa buku Anda) yang memungkinkan konversi yang mudah dari bentuk persegi panjang ke bentuk kutub, (R → P) dan kembali dari bentuk kutub ke bentuk persegi panjang, (R → P).

Bilangan Kompleks dengan Rumus Eksponensial

Sejauh ini kita telah mempelajari bilangan kompleks dalam Rumus Rectangular, (a + jb) dan Rumus Polar, (A ∠ ± θ). Tetapi ada juga metode ketiga untuk mewakili bilangan kompleks yang mirip dengan bentuk kutub yang sesuai dengan panjang (besarnya) dan sudut fasa sinusoidal tetapi menggunakan dasar logaritma asli, e = 2,718 281. untuk menemukan nilai bilangan kompleks. Metode ketiga ini disebut rumus Eksponensial .

Rumus eksponensial menggunakan fungsi trigonometri dari kedua sinus (sin) dan cosinus (cos) nilai-nilai dari segitiga siku kanan untuk menentukan eksponensial kompleks sebagai titik berputar di kompleks pesawat. Rumus eksponensial untuk menemukan posisi titik didasarkan pada rumus Euler's, dinamai sesuai matematikawan Swiss, Leonhard Euler dan diberikan sebagai:

Rumus Eksponensial
Z = Ae^jΦ
Z = A(cos Φ + jsinΦ) 

Kemudian Rumus Euler dapat diwakili oleh diagram fasor berputar berikut pada bidang kompleks.

Kita dapat melihat bahwa Rumus Euler sangat mirip dengan rumus kutub di atas dan itu menunjukkan kepada kita bahwa bilangan seperti Ae^jθ yang memiliki besaran 1 juga bilangan kompleks.

Kita tidak hanya dapat mengkonversi bilangan kompleks yang berada dalam bentuk eksponensial dengan mudah menjadi bentuk kutub seperti: 2e^j30 = 2∠30, 10e^j120 = 10∠120 atau -6e^j90 = -6∠90, tetapi rumus Euler juga memberikan kita cara mengubah bilangan kompleks dari bentuk eksponensial menjadi bentuk persegi panjangnya. Kemudian hubungan antara, bentuk eksponensial, kutub dan persegi panjang dalam mendefinisikan bilangan kompleks diberikan sebagai.

Rumus Bilangan Kompleks

Z = x + jy = A∠θ = A(cosΦ + jsinΦ)

Notasi Fasor

Sejauh ini kita telah melihat berbagai cara untuk merepresentasikan vektor berputar atau vektor stasioner menggunakan bilangan kompleks untuk menentukan titik pada bidang kompleks.

Notasi phasor adalah proses membangun bilangan kompleks tunggal yang memiliki amplitudo dan sudut fasa dari bentuk gelombang sinusoidal yang diberikan. Kemudian notasi fasor atau transformasi fasor seperti yang kadang-kadang disebut, mentransfer bagian nyata dari fungsi sinusoidal: A_(t) = A_m cos (ωt ± Φ) dari domain waktu ke domain bilangan kompleks yang juga disebut domain frekuensi. Sebagai contoh:

Harap dicatat bahwa √2 mengubah amplitudo maksimum menjadi nilai efektif atau RMS dengan sudut fasa yang diberikan dalam radian, (ω).

Ringkasan Bilangan Kompleks

Kemudian untuk meringkas tutorial ini tentang Bilangan Kompleks dan penggunaan bilangan kompleks dalam teknik listrik.

• Bilangan Kompleks terdiri dari dua bilangan berbeda, bilangan real plus bilangan imajiner.
• Bilangan imajiner dibedakan dari bilangan real dengan menggunakan operator-j.
• Nomor dengan huruf " j " di depannya mengidentifikasinya sebagai nomor imajiner di bidang kompleks.
• Menurut definisi, j-operator j ≡ √-1
• Bilangan imajiner dapat ditambahkan, dikurangi, dikalikan dan dibagi sama dengan bilangan real.
• Pengkalian " j " dengan " j " menghasilkan j² = -1
• Dalam Bentuk/rumus Persegi Panjang bilangan kompleks diwakili oleh titik di ruang pada bidang kompleks.
• Dalam Bentuk/rumus Kutub bilangan kompleks diwakili oleh garis yang panjangnya adalah amplitudo dan oleh sudut fasa.
• Dalam Bentuk/rumus Eksponensial bilangan kompleks diwakili oleh garis dan sudut yang sesuai yang menggunakan dasar logaritma natural.
• Bilangan kompleks dapat direpresentasikan dalam satu dari tiga cara:

Z = x + jy  » Bentuk Rectangular
Z = A ∠Φ  » Bentuk Polar
Z = A e^jΦ  » Bentuk eksponensial

• Rumus Euler dapat digunakan untuk mengubah Bilangan Kompleks dari bentuk eksponensial menjadi bentuk persegi panjang.

Dalam tutorial sebelumnya termasuk yang ini kita telah melihat bahwa kita dapat menggunakan fasor untuk mewakili bentuk gelombang sinusoidal dan bahwa amplitudo dan sudut fasa dapat ditulis dalam bentuk bilangan kompleks.

Kita juga telah melihat bahwa Bilangan Kompleks dapat disajikan dalam bentuk persegi panjang, kutub atau eksponensial dengan konversi antara setiap bentuk aljabar bilangan kompleks termasuk penambahan, pengurangan, perkalian dan pembagian.

Dalam beberapa tutorial berikutnya yang berkaitan dengan hubungan fasor dalam Rangkaian AC Seri, kita akan melihat impedansi dari beberapa komponen rangkaian pasif umum dan menggambar diagram fasor untuk arus yang mengalir melalui komponen dan tegangan yang diterapkan di mulai dengan Resistansi AC.

Berbagi :