Diagram Fasor dan Aljabar Fasor
Diagram Fasor adalah cara grafis untuk mewakili besarnya dan hubungan terarah antara dua atau lebih kuantitas bolak-balik. Bentuk gelombang sinusoidal dengan frekuensi yang sama dapat memiliki Perbedaan Fasa di antara mereka yang mewakili perbedaan sudut dari dua bentuk gelombang sinusoidal.
Juga istilah "lead/memimpin" dan "lag/tertinggal" serta "in-phase/dalam-fasa" dan "out-of-phase/diluar-fasa" umumnya digunakan untuk menunjukkan hubungan satu gelombang dengan yang lain dengan ekspresi sinusoidal umum yang diberikan sebagai: A(t) = Am sin(ωt ± Φ) mewakili sinusoidal dalam bentuk domain waktu.
Tetapi ketika disajikan secara matematis dengan cara ini kadang-kadang sulit untuk memvisualisasikan perbedaan sudut atau fasor ini antara dua atau lebih bentuk gelombang sinusoidal. Salah satu cara untuk mengatasi masalah ini adalah dengan merepresentasikan sinusoidal secara grafis dalam bentuk spasial atau domain-fasor dengan menggunakan Diagram Fasor, dan ini dicapai dengan metode vektor berputar/rotasi.
Pada dasarnya vektor yang berputar, hanya disebut " Fasor" adalah garis berskala yang panjangnya mewakili kuantitas AC yang memiliki besaran ("amplitudo puncak") dan arah ("fasa") yang "beku" pada suatu titik waktu. Sebuah fasor adalah vektor yang memiliki kepala panah di satu ujung yang menandakan sebagian nilai maksimum kuantitas vektor (V atau I) dan sebagian ujung vektor yang berputar.
Secara umum, vektor diasumsikan berporos pada salah satu ujung di sekitar titik nol tetap yang dikenal sebagai "titik asal" sedangkan ujung panah menunjukkan kuantitas, berputar bebas dalam arah berlawanan arah jarum jam pada kecepatan sudut, ( ω ) dari satu penuh revolusi untuk setiap siklus.
Rotasi berlawanan arah jarum jam dari vektor ini dianggap sebagai rotasi positif. Demikian juga, rotasi searah jarum jam dianggap sebagai rotasi negatif.
Walaupun kedua istilah vektor dan fasor dipakai untuk menggambarkan garis berputar yang mempunyai besaran nilai dan juga arah, perbedaan yang utama diantara keduanya yaitu pada besarnya vektor adalah "nilai puncak" dari sinusoidal sedangkan besarnya fasor adalah " nilai rms ”dari sinusoidal. Dalam kedua kasus, sudut fasa dan arah tetap sama.
Fasa kuantitas bergantian setiap saat dapat diwakili oleh diagram fasor, sehingga diagram fasor dapat dianggap sebagai "fungsi waktu". Gelombang sinusoidal lengkap dapat dibangun oleh vektor tunggal yang berputar pada kecepatan sudut ω = 2πƒ , di mana ƒ adalah frekuensi bentuk gelombang. Maka Fasor adalah kuantitas yang memiliki "Magnitude" dan "Direction".
Secara umum, ketika membuat diagram fasor, kecepatan sudut dari gelombang sinusoidal selalu diasumsikan sebagai: ω dalam rad/detik. Perhatikan diagram fasor di bawah ini.
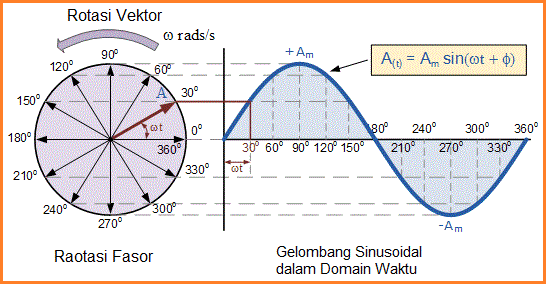
Ketika vektor tunggal berputar dalam arah berlawanan arah jarum jam, ujungnya pada titik A akan memutar satu putaran penuh 360° atau 2π yang mewakili satu siklus lengkap. Jika panjang ujung bergeraknya ditransfer pada interval sudut yang berbeda dalam waktu ke grafik seperti yang ditunjukkan di atas, bentuk gelombang sinusoidal akan ditarik mulai dari kiri dengan nol waktu.
Setiap posisi sepanjang sumbu horizontal menunjukkan waktu yang telah berlalu sejak nol waktu, t = 0. Ketika vektor horisontal, ujung vektor mewakili sudut 0°, 180° dan 360°. Demikian juga, ketika ujung vektor vertikal itu mewakili nilai puncak positif, (+Am) pada 90° atau π/2 dan nilai puncak negatif, (-Am) pada 270° atau 3π/2.
Kemudian sumbu waktu dari bentuk gelombang mewakili sudut baik dalam derajat atau radian di mana fasor telah bergerak. Jadi kita dapat mengatakan bahwa fasor mewakili tegangan skala atau nilai arus dari vektor yang berputar yang “beku” di beberapa titik waktu, ( t ) dan dalam contoh kita di atas, ini berada pada sudut 30°.
Kadang-kadang ketika kita menganalisis bentuk gelombang bolak-balik, kita mungkin perlu mengetahui posisi fasor, mewakili Kuantitas Bergantian pada waktu tertentu, terutama ketika kita ingin membandingkan dua bentuk gelombang berbeda pada sumbu yang sama. Misalnya, tegangan dan arus. Kami mengasumsikan dalam bentuk gelombang di atas bahwa bentuk gelombang dimulai pada waktu t = 0 dengan sudut fasa yang sesuai dalam derajat atau radian.
Tetapi jika bentuk gelombang kedua mulai ke kiri atau ke kanan dari titik nol ini atau kami ingin mewakili dalam notasi fasor hubungan antara dua bentuk gelombang maka kita perlu memperhitungkan perbedaan fasa ini, Φ dari bentuk gelombang.
Pertimbangkan diagram di bawah ini dari tutorial Perbedaan Fasa sebelumnya .
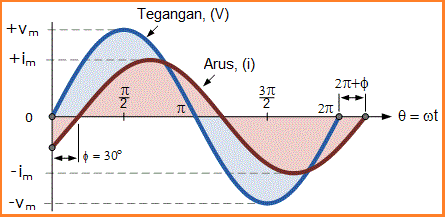
Ekspresi matematika umum untuk menentukan dua kuantitas sinusoidal ini akan ditulis sebagai:
v(t) = Vm sin (ωt)
i(t) = Im sin (ωt-Φ)
Arus, i tertinggal oleh tegangan, v dari sudut Φ dan dalam contoh kita di atas ini adalah 30°. Jadi perbedaan antara dua fasor yang mewakili dua kuantitas sinusoidal adalah sudut Φ dan diagram fasor yang dihasilkan akan.
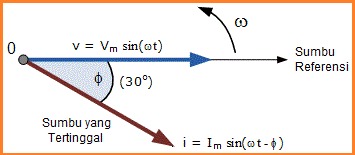
Diagram fasor digambar sesuai dengan waktu nol ( t = 0 ) pada sumbu horizontal. Panjang fasor sebanding dengan nilai voltase, (V) dan arus, (I) pada saat waktu diagram diagram fasor dibuat. Fasor arus tertinggal fasor tegangan dengan sudut, Φ , ketika dua fasor berputar dalam arah berlawanan arah jarum jam seperti yang dinyatakan sebelumnya, oleh karena itu sudut, Φ juga diukur dalam arah berlawanan arah jarum jam yang sama.
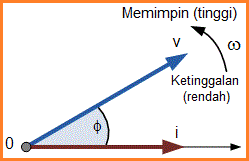
Namun jika bentuk gelombang dibekukan pada waktu, t = 30°, diagram fasor yang sesuai akan terlihat seperti yang ditunjukkan di sebelah kanan. Sekali lagi fasor arus tertinggal di belakang fasor tegangan karena dua bentuk gelombang memiliki frekuensi yang sama.
Namun, saat gelombang arus melintasi garis sumbu nol horizontal pada arus, kita dapat menggunakan fasor arus sebagai referensi baru dan dengan benar mengatakan bahwa fasor tegangan “memimpin” fasor arus dengan sudut, Φ. Bagaimanapun juga, satu fasor ditetapkan sebagai fasor referensi dan semua fasor lainnya akan memimpin atau tertinggal sehubungan dengan referensi ini.

Dengan menggambar dua fasor untuk skala ke kertas grafik, jumlah fasornya V1 + V2 dapat dengan mudah ditemukan dengan mengukur panjang garis diagonal, yang dikenal sebagai "resultan r-vektor", dari titik nol ke persimpangan dari garis konstruksi 0-A .
Kelemahan dari metode grafis ini adalah bahwa hal itu memakan waktu ketika menggambar skala untuk mengukur. Selain itu, walaupun metode grafis ini memberikan jawaban yang cukup akurat untuk sebagian besar tujuan, metode ini dapat menghasilkan kesalahan jika tidak ditarik dengan akurat atau dengan benar ke skala.
Maka salah satu cara untuk memastikan bahwa jawaban yang benar selalu diperoleh adalah dengan metode analitik. Secara matematis kita dapat menambahkan dua tegangan bersama-sama dengan terlebih dahulu mencari mereka “vertikal” dan “horizontal” arah, dan dari ini kita dapat menghitung baik “vertikal” dan “horizontal” komponen untuk resultan “vektor r”, VT.
Metode analitik ini yang menggunakan aturan cosinus dan sinus untuk menemukan nilai resultan ini biasa disebut Rumus Rectangular . Dalam bentuk persegi panjang, fasor dibagi menjadi bagian nyata, x dan bagian imajiner, y membentuk ekspresi umum Z = x ± jy. (kami akan membahas ini secara lebih rinci di tutorial berikutnya). Ini kemudian memberi kita ekspresi matematis yang mewakili besarnya dan fasa tegangan sinusoidal sebagai:
Tegangan yang dihasilkan, VT ditemukan dengan menambahkan bersama-sama komponen horisontal dan vertikal sebagai berikut.
Sekarang kedua nilai-nilai nyata dan imajiner telah ditemukan besarnya tegangan, VT ditentukan dengan hanya menggunakan Pythagoras Teorema untuk 90° segitiga sebagai berikut.



Kali ini alih-alih "menambahkan" bersama-sama komponen horisontal dan vertikal yang kita ambil, kurangi.
Seperti halnya fasa-fasa tunggal di atas, fasor-fasor yang mewakili sistem tiga fasa juga berputar dalam arah berlawanan jarum jam di sekitar titik pusat seperti yang ditunjukkan oleh panah bertanda ω dalam rad/s. Fasor untuk sistem seimbang star tiga fasa atau terhubung delta ditunjukkan di bawah ini.

Tegangan fasa semua sama besarnya tetapi hanya berbeda dalam sudut fasa mereka. Tiga belitan kumparan dihubungkan bersama pada titik-titik, a1, b1 dan c1 untuk menghasilkan hubungan netral umum untuk tiga fasa individu. Kemudian jika fasa merah diambil sebagai fasa referensi masing-masing tegangan fasa individu dapat didefinisikan sehubungan dengan netral sebagai.
Juga istilah "lead/memimpin" dan "lag/tertinggal" serta "in-phase/dalam-fasa" dan "out-of-phase/diluar-fasa" umumnya digunakan untuk menunjukkan hubungan satu gelombang dengan yang lain dengan ekspresi sinusoidal umum yang diberikan sebagai: A(t) = Am sin(ωt ± Φ) mewakili sinusoidal dalam bentuk domain waktu.
Tetapi ketika disajikan secara matematis dengan cara ini kadang-kadang sulit untuk memvisualisasikan perbedaan sudut atau fasor ini antara dua atau lebih bentuk gelombang sinusoidal. Salah satu cara untuk mengatasi masalah ini adalah dengan merepresentasikan sinusoidal secara grafis dalam bentuk spasial atau domain-fasor dengan menggunakan Diagram Fasor, dan ini dicapai dengan metode vektor berputar/rotasi.
Pada dasarnya vektor yang berputar, hanya disebut " Fasor" adalah garis berskala yang panjangnya mewakili kuantitas AC yang memiliki besaran ("amplitudo puncak") dan arah ("fasa") yang "beku" pada suatu titik waktu. Sebuah fasor adalah vektor yang memiliki kepala panah di satu ujung yang menandakan sebagian nilai maksimum kuantitas vektor (V atau I) dan sebagian ujung vektor yang berputar.
Secara umum, vektor diasumsikan berporos pada salah satu ujung di sekitar titik nol tetap yang dikenal sebagai "titik asal" sedangkan ujung panah menunjukkan kuantitas, berputar bebas dalam arah berlawanan arah jarum jam pada kecepatan sudut, ( ω ) dari satu penuh revolusi untuk setiap siklus.
Rotasi berlawanan arah jarum jam dari vektor ini dianggap sebagai rotasi positif. Demikian juga, rotasi searah jarum jam dianggap sebagai rotasi negatif.
Walaupun kedua istilah vektor dan fasor dipakai untuk menggambarkan garis berputar yang mempunyai besaran nilai dan juga arah, perbedaan yang utama diantara keduanya yaitu pada besarnya vektor adalah "nilai puncak" dari sinusoidal sedangkan besarnya fasor adalah " nilai rms ”dari sinusoidal. Dalam kedua kasus, sudut fasa dan arah tetap sama.
Fasa kuantitas bergantian setiap saat dapat diwakili oleh diagram fasor, sehingga diagram fasor dapat dianggap sebagai "fungsi waktu". Gelombang sinusoidal lengkap dapat dibangun oleh vektor tunggal yang berputar pada kecepatan sudut ω = 2πƒ , di mana ƒ adalah frekuensi bentuk gelombang. Maka Fasor adalah kuantitas yang memiliki "Magnitude" dan "Direction".
Secara umum, ketika membuat diagram fasor, kecepatan sudut dari gelombang sinusoidal selalu diasumsikan sebagai: ω dalam rad/detik. Perhatikan diagram fasor di bawah ini.
Diagram Fasor dari Gelombang Sinusoidal

Ketika vektor tunggal berputar dalam arah berlawanan arah jarum jam, ujungnya pada titik A akan memutar satu putaran penuh 360° atau 2π yang mewakili satu siklus lengkap. Jika panjang ujung bergeraknya ditransfer pada interval sudut yang berbeda dalam waktu ke grafik seperti yang ditunjukkan di atas, bentuk gelombang sinusoidal akan ditarik mulai dari kiri dengan nol waktu.
Setiap posisi sepanjang sumbu horizontal menunjukkan waktu yang telah berlalu sejak nol waktu, t = 0. Ketika vektor horisontal, ujung vektor mewakili sudut 0°, 180° dan 360°. Demikian juga, ketika ujung vektor vertikal itu mewakili nilai puncak positif, (+Am) pada 90° atau π/2 dan nilai puncak negatif, (-Am) pada 270° atau 3π/2.
Kemudian sumbu waktu dari bentuk gelombang mewakili sudut baik dalam derajat atau radian di mana fasor telah bergerak. Jadi kita dapat mengatakan bahwa fasor mewakili tegangan skala atau nilai arus dari vektor yang berputar yang “beku” di beberapa titik waktu, ( t ) dan dalam contoh kita di atas, ini berada pada sudut 30°.
Kadang-kadang ketika kita menganalisis bentuk gelombang bolak-balik, kita mungkin perlu mengetahui posisi fasor, mewakili Kuantitas Bergantian pada waktu tertentu, terutama ketika kita ingin membandingkan dua bentuk gelombang berbeda pada sumbu yang sama. Misalnya, tegangan dan arus. Kami mengasumsikan dalam bentuk gelombang di atas bahwa bentuk gelombang dimulai pada waktu t = 0 dengan sudut fasa yang sesuai dalam derajat atau radian.
Tetapi jika bentuk gelombang kedua mulai ke kiri atau ke kanan dari titik nol ini atau kami ingin mewakili dalam notasi fasor hubungan antara dua bentuk gelombang maka kita perlu memperhitungkan perbedaan fasa ini, Φ dari bentuk gelombang.
Pertimbangkan diagram di bawah ini dari tutorial Perbedaan Fasa sebelumnya .
Beda Fasa Bentuk Gelombang Sinusoidal

Ekspresi matematika umum untuk menentukan dua kuantitas sinusoidal ini akan ditulis sebagai:
v(t) = Vm sin (ωt)
i(t) = Im sin (ωt-Φ)
Arus, i tertinggal oleh tegangan, v dari sudut Φ dan dalam contoh kita di atas ini adalah 30°. Jadi perbedaan antara dua fasor yang mewakili dua kuantitas sinusoidal adalah sudut Φ dan diagram fasor yang dihasilkan akan.
Diagram Fasor dari Gelombang Sinusoidal

Diagram fasor digambar sesuai dengan waktu nol ( t = 0 ) pada sumbu horizontal. Panjang fasor sebanding dengan nilai voltase, (V) dan arus, (I) pada saat waktu diagram diagram fasor dibuat. Fasor arus tertinggal fasor tegangan dengan sudut, Φ , ketika dua fasor berputar dalam arah berlawanan arah jarum jam seperti yang dinyatakan sebelumnya, oleh karena itu sudut, Φ juga diukur dalam arah berlawanan arah jarum jam yang sama.

Namun jika bentuk gelombang dibekukan pada waktu, t = 30°, diagram fasor yang sesuai akan terlihat seperti yang ditunjukkan di sebelah kanan. Sekali lagi fasor arus tertinggal di belakang fasor tegangan karena dua bentuk gelombang memiliki frekuensi yang sama.
Namun, saat gelombang arus melintasi garis sumbu nol horizontal pada arus, kita dapat menggunakan fasor arus sebagai referensi baru dan dengan benar mengatakan bahwa fasor tegangan “memimpin” fasor arus dengan sudut, Φ. Bagaimanapun juga, satu fasor ditetapkan sebagai fasor referensi dan semua fasor lainnya akan memimpin atau tertinggal sehubungan dengan referensi ini.
Penambahan Fasor
Kadang-kadang perlu ketika mempelajari sinusoidal untuk menambahkan bersama dua bentuk gelombang bolak-balik, misalnya dalam rangkaian seri AC, yang tidak dalam fasa satu sama lain. Jika mereka berada dalam fasa yaitu, tidak ada pergeseran fasa maka mereka dapat ditambahkan bersama dengan cara yang sama seperti nilai DC untuk menemukan jumlah aljabar dari dua vektor.
Sebagai contoh, jika dua tegangan katakanlah 50 volt dan 25 volt masing-masing bersama-sama "dalam-fasa", mereka akan menambah atau menjumlahkan bersama-sama untuk membentuk satu tegangan 75 volt (50 + 25).
Sebagai contoh, jika dua tegangan katakanlah 50 volt dan 25 volt masing-masing bersama-sama "dalam-fasa", mereka akan menambah atau menjumlahkan bersama-sama untuk membentuk satu tegangan 75 volt (50 + 25).
Namun, jika mereka tidak berada dalam fasa yaitu, mereka tidak memiliki arah atau titik awal yang sama maka sudut fasa di antara mereka perlu diperhitungkan sehingga mereka ditambahkan bersama-sama menggunakan diagram fasor untuk menentukan Fasor atau Vektor Hasil resultan mereka dengan menggunakan hukum jajaran genjang .
Pertimbangkan dua tegangan AC, V1 memiliki tegangan puncak 20 volt, dan V2 memiliki tegangan puncak 30 volt di mana V1 mengarah V2 sebesar 60°.
Tegangan total, VT dari dua tegangan dapat ditemukan dengan terlebih dahulu menggambar diagram fasor yang mewakili dua vektor dan kemudian membangun genjang di mana dua dari sisi adalah tegangan, V1 dan V2 seperti yang ditunjukkan di bawah ini.
Tegangan total, VT dari dua tegangan dapat ditemukan dengan terlebih dahulu menggambar diagram fasor yang mewakili dua vektor dan kemudian membangun genjang di mana dua dari sisi adalah tegangan, V1 dan V2 seperti yang ditunjukkan di bawah ini.
Penambahan Fasor dari dua Fasor

Dengan menggambar dua fasor untuk skala ke kertas grafik, jumlah fasornya V1 + V2 dapat dengan mudah ditemukan dengan mengukur panjang garis diagonal, yang dikenal sebagai "resultan r-vektor", dari titik nol ke persimpangan dari garis konstruksi 0-A .
Kelemahan dari metode grafis ini adalah bahwa hal itu memakan waktu ketika menggambar skala untuk mengukur. Selain itu, walaupun metode grafis ini memberikan jawaban yang cukup akurat untuk sebagian besar tujuan, metode ini dapat menghasilkan kesalahan jika tidak ditarik dengan akurat atau dengan benar ke skala.
Maka salah satu cara untuk memastikan bahwa jawaban yang benar selalu diperoleh adalah dengan metode analitik. Secara matematis kita dapat menambahkan dua tegangan bersama-sama dengan terlebih dahulu mencari mereka “vertikal” dan “horizontal” arah, dan dari ini kita dapat menghitung baik “vertikal” dan “horizontal” komponen untuk resultan “vektor r”, VT.
Metode analitik ini yang menggunakan aturan cosinus dan sinus untuk menemukan nilai resultan ini biasa disebut Rumus Rectangular . Dalam bentuk persegi panjang, fasor dibagi menjadi bagian nyata, x dan bagian imajiner, y membentuk ekspresi umum Z = x ± jy. (kami akan membahas ini secara lebih rinci di tutorial berikutnya). Ini kemudian memberi kita ekspresi matematis yang mewakili besarnya dan fasa tegangan sinusoidal sebagai:
Definisi Sinusoidal Kompleks
vm = cos (Φ) + jVm sin (sinΦ)
Jadi penambahan dua vektor, A dan B menggunakan ekspresi umum sebelumnya adalah sebagai berikut:
A = x + jy
B = w + jz
A+B = (x+w) + j(y+z)
B = w + jz
A+B = (x+w) + j(y+z)
Penambahan Fasor menggunakan Bentuk Rectangular
Tegangan, V2 dari 30 volt menunjuk ke arah referensi sepanjang sumbu nol horisontal, maka ia memiliki komponen horisontal tetapi tidak ada komponen vertikal sebagai berikut.
- Komponen Horisontal = 30 cos 0° = 30 volt
- Komponen Vertikal = 30 sin 0° = 0 volt
Hal ini kemudian memberi kita ekspresi segi empat untuk tegangan V2 dari: 30 + j0
Tegangan, V1 dari 20 volt mengarah tegangan, V2 oleh 60°, maka memiliki komponen horisontal dan vertikal sebagai berikut.
- Komponen Horisontal = 20 cos 60° = 20 x 0,5 = 10 volt
- Komponen Vertikal = 20 sin 60° = 20 x 0,866 = 17,32 volt
Ini kemudian memberi kita ekspresi persegi panjang untuk tegangan V1 dari: 10 + j17.32
Tegangan yang dihasilkan, VT ditemukan dengan menambahkan bersama-sama komponen horisontal dan vertikal sebagai berikut.
VHorisontal = jumlah bagian nyata dari V1 dan V2 = 30 + 10 = 40 volt
VVertikal = jumlah bagian imajiner dari V1 dan V2 = 0 + 17,32 = 17,32 volt
Sekarang kedua nilai-nilai nyata dan imajiner telah ditemukan besarnya tegangan, VT ditentukan dengan hanya menggunakan Pythagoras Teorema untuk 90° segitiga sebagai berikut.

Maka diagram fasor yang dihasilkan adalah:
Nilai yang dihasilkan dari VT

Pengurangan Fasor
Fasor pengurangan sangat mirip dengan metode persegi panjang di atas Selain itu, kecuali kali ini perbedaan vektor adalah diagonal lain dari genjang antara dua tegangan dari V1 dan V2 seperti yang ditunjukkan.
Pengurangan Vektor dari dua Fasor

Kali ini alih-alih "menambahkan" bersama-sama komponen horisontal dan vertikal yang kita ambil, kurangi.
A = x + jy
B = w + jz
A+B = (x-w) + j(y-z)
B = w + jz
A+B = (x-w) + j(y-z)
Diagram Fasor 3 Fasa
Sebelumnya kita hanya melihat bentuk gelombang AC fasa tunggal di mana coil multi-putaran berputar dalam medan magnet. Tetapi jika tiga kumparan identik masing-masing dengan jumlah yang sama coil bergantian ditempatkan pada sudut listrik 120° satu sama lain pada poros rotor yang sama, pasokan tegangan tiga fasa akan dihasilkan.
Sebuah tiga fasa supply tegangan yang seimbang terdiri dari tiga tegangan sinusoidal individu yang semuanya sama besarnya dan frekuensi tetapi out-of-fasa satu sama lain dengan persis 120° derajat listrik. Standar praktis adalah dengan mewarnai kode tiga fasa tersebut seperti Merah, Kuning dan Biru untuk mengidentifikasi setiap fasa individu dengan fasa merah sebagai fasa referensi. Urutan rotasi normal untuk supply tiga fasa adalah Red diikuti oleh Yellow dan Blue, (R, Y, B).
Seperti halnya fasa-fasa tunggal di atas, fasor-fasor yang mewakili sistem tiga fasa juga berputar dalam arah berlawanan jarum jam di sekitar titik pusat seperti yang ditunjukkan oleh panah bertanda ω dalam rad/s. Fasor untuk sistem seimbang star tiga fasa atau terhubung delta ditunjukkan di bawah ini.
Diagram Fasor tiga fasa

Tegangan fasa semua sama besarnya tetapi hanya berbeda dalam sudut fasa mereka. Tiga belitan kumparan dihubungkan bersama pada titik-titik, a1, b1 dan c1 untuk menghasilkan hubungan netral umum untuk tiga fasa individu. Kemudian jika fasa merah diambil sebagai fasa referensi masing-masing tegangan fasa individu dapat didefinisikan sehubungan dengan netral sebagai.
Persamaan Tegangan Tiga Fasa
Red Phase: VRN = Vm sinθ
Yellow Phase: VYN = Vm sin(θ-120°)
Blue Phase: VBN = Vm sin(θ-240°)
atau
VBN = Vm sin(θ+120°)
Jika tegangan fasa-merah, VRN diambil sebagai tegangan referensi seperti yang dinyatakan sebelumnya maka urutan fasa akan menjadi R - Y - B sehingga tegangan pada fasa-kuning tertinggal VRN sampai 120°, dan tegangan pada fasa-biru tertinggal. VYN juga oleh 120°. Tapi kita juga bisa mengatakan tegangan fasa-biru, VBN memimpin tegangan fasa-merah, VRN hingga 120°.
Satu hal terakhir tentang sistem tiga fasa. Karena tiga tegangan sinusoidal masing-masing memiliki hubungan tetap antara satu sama lain dari 120° maka dikatakan "seimbang" oleh karena itu, dalam satu set tegangan tiga fasa seimbang, jumlah fasor mereka akan selalu nol seperti: Va + Vb + Vc = 0
Yellow Phase: VYN = Vm sin(θ-120°)
Blue Phase: VBN = Vm sin(θ-240°)
atau
VBN = Vm sin(θ+120°)
Jika tegangan fasa-merah, VRN diambil sebagai tegangan referensi seperti yang dinyatakan sebelumnya maka urutan fasa akan menjadi R - Y - B sehingga tegangan pada fasa-kuning tertinggal VRN sampai 120°, dan tegangan pada fasa-biru tertinggal. VYN juga oleh 120°. Tapi kita juga bisa mengatakan tegangan fasa-biru, VBN memimpin tegangan fasa-merah, VRN hingga 120°.
Satu hal terakhir tentang sistem tiga fasa. Karena tiga tegangan sinusoidal masing-masing memiliki hubungan tetap antara satu sama lain dari 120° maka dikatakan "seimbang" oleh karena itu, dalam satu set tegangan tiga fasa seimbang, jumlah fasor mereka akan selalu nol seperti: Va + Vb + Vc = 0
Ringkasan Diagram Fasor
Kemudian untuk merangkum tutorial ini tentang Diagram Fasor.
Dalam istilah yang paling sederhana, diagram fasor adalah proyeksi dari vektor yang berputar ke sumbu horizontal yang mewakili nilai sesaat. Karena diagram fasor dapat digambarkan untuk mewakili setiap saat waktu dan oleh karena itu sudut apa pun, fasor referensi dari kuantitas bolak-balik selalu ditarik sepanjang arah sumbu x positif.
- Vektor, Fasor dan Diagram Fasor HANYA berlaku untuk jumlah bolak-balik AC sinusoidal.
- Diagram Fasor dapat digunakan untuk mewakili dua atau lebih jumlah sinusoidal stasioner setiap saat.
- Umumnya fasor referensi digambar di sepanjang sumbu horisontal dan pada saat itu juga fasor lainnya ditarik.
- Semua fasor digambarkan dengan mengacu pada sumbu nol horisontal. Diagram Fasor dapat ditarik untuk mewakili lebih dari dua sinusoidal. Mereka dapat berupa tegangan, arus, atau kuantitas bolak-balik lainnya tetapi frekuensinya semuanya harus sama.
- Semua fasa ditarik berputar dalam arah berlawanan arah jarum jam. Semua fasor sebelum fasor referensi dikatakan "leading/memimpin" sementara semua fasor di belakang fasor referensi dikatakan "lagging/tertinggal".
- Secara umum, panjang fasor mewakili nilai rms dari jumlah sinusoidal daripada nilai maksimumnya.
- Sinusoidal dengan frekuensi berbeda tidak dapat direpresentasikan pada diagram fasor yang sama karena kecepatan vektor yang berbeda. Setiap saat dalam waktu sudut fasa di antara mereka akan berbeda.
- Dua atau lebih vektor dapat ditambahkan atau dikurangkan bersama dan menjadi vektor tunggal, yang disebut Vektor Hasil (Resultant Vector).
- Sisi horizontal vektor sama dengan vektor nyata atau "x". Sisi vertikal vektor sama dengan vektor imajiner atau "y". Sisi miring dari sudut siku-siku yang dihasilkan adalah setara dengan vektor "r".
- Dalam sistem seimbang tiga fasa, masing-masing fasor individu dipindahkan dengan 120°.
Dalam tutorial berikutnya tentang Teori AC kita akan melihat bentuk gelombang sinusoidal sebagai Bilangan Kompleks dalam bentuk Persegi Panjang, bentuk Kutub dan bentuk Eksponensial.