Tegangan Rata-rata
Setelah membahas nilai Tegangan RMS dari bentuk gelombang bolak-balik pada tutorial sebelumnya, sekarang kita dapat belajar menghitung nilai lain menggunakan rumus pertengahan-ordinat atau rumus analitik untuk menemukan bentuk gelombang "rata-rata" atau nilai tegangan rata-rata.
Dalam tutorial ini kita akan belajar menghitung "rata-rata" atau nilai tegangan rata-rata dari bentuk gelombang sinusoidal menggunakan rumus mid-ordinat dan rumus analitik. Proses yang digunakan untuk menemukan Tegangan Rata-rata dari gelombang bolak-balik sangat mirip dengan yang untuk menemukan nilai RMS-nya, perbedaan kali ini adalah bahwa nilai sesaat tidak kuadrat dan kami tidak menemukan akar kuadrat dari rangkuman rata-rata.
Tegangan atau Arus rata-rata dari suatu gelombang periodik apakah itu gelombang sinusoidal, gelombang persegi atau gelombang segitiga didefinisikan sebagai: "hasil bagi dari daerah di bawah bentuk gelombang sehubungan dengan waktu". Dengan kata lain, rata-rata semua nilai sesaat sepanjang sumbu waktu dengan waktu menjadi satu periode penuh, ( T ).
Untuk bentuk gelombang periodik, area di atas sumbu horizontal positif sedangkan area di bawah sumbu horizontal negatif. Hasilnya adalah bahwa nilai rata-rata atau rata-rata kuantitas bolak-balik simetris adalah nol, (0) karena area di atas sumbu horizontal (setengah siklus positif) sama dengan area di bawah sumbu (setengah siklus negatif) dan dengan demikian membatalkan satu sama lain.
Ini karena ketika kita melakukan perhitungan matematika dari dua area, area negatif membatalkan area positif yang menghasilkan tegangan rata-rata nol. Maka nilai rata-rata atau rata-rata dari kuantitas bolak-balik simetris, seperti gelombang sinusoidal, adalah nilai rata-rata yang diukur hanya setengah dari siklus, karena seperti yang baru saja kami nyatakan, nilai rata-rata selama satu siklus lengkap adalah nol terlepas dari amplitudo puncak.
Istilah dalam kelistrikan Tegangan rata-rata atau Arus rata-rata, dapat digunakan dalam analisis atau perhitungan rangkaian AC dan DC. Simbol yang digunakan untuk mewakili nilai rata-rata didefinisikan sebagai: VAV atau IAV.
Setengah positif dari gelombang dibagi menjadi sejumlah "n" bagian yang sama atau pertengahan-ordinat. Lebar setiap pertengahan-ordinat akan menjadi n° derajat (atau t detik) dan tinggi setiap pertengahan-ordinat akan sama dengan nilai sesaat dari bentuk gelombang pada titik itu sepanjang sumbu x dari bentuk gelombang.
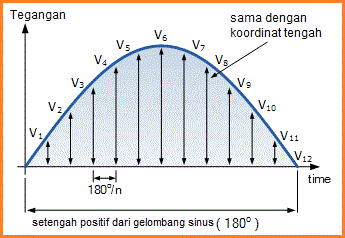
Setiap nilai pertengahan-ordinat dari bentuk gelombang tegangan ditambahkan ke depan dan total dijumlahkan, V1 ke V12 dibagi dengan jumlah mid-kordinat digunakan untuk memberi kita “ Tegangan rata-rata”. Kemudian tegangan rata-rata (VAV) adalah jumlah rata-rata dari pertengahan-ordinat dari gelombang tegangan dan diberikan sebagai:

dan untuk contoh sederhana kami di atas, tegangan rata-rata karena itu dihitung sebagai:

Jadi seperti sebelumnya mari kita asumsikan lagi bahwa tegangan bolak-balik 20 volt puncak bervariasi selama satu setengah siklus sebagai berikut:
Nilai tegangan rata - rata karena itu dihitung sebagai:

Kemudian nilai Tegangan rata-rata untuk satu setengah siklus menggunakan metode grafis diberikan sebagai: 12,64 Volts .
Nilai rata-rata dapat diambil secara matematis dengan mengambil perkiraan area di bawah kurva pada berbagai interval dengan jarak atau panjang pangkalan dan ini dapat dilakukan dengan menggunakan segitiga atau persegi panjang seperti yang ditunjukkan.
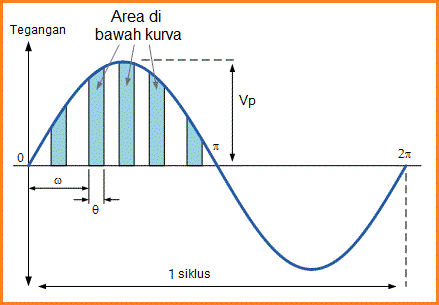
Dengan mendekati area persegi panjang di bawah kurva, kita dapat memperoleh gambaran kasar dari area aktual masing-masing. Dengan menambahkan bersama semua bidang ini, nilai rata-rata dapat ditemukan. Jika jumlah tak terbatas dari persegi panjang tipis yang lebih kecil digunakan, yang lebih akurat akan menjadi hasil akhir saat mendekati 2/π.
Area di bawah kurva dapat ditemukan dengan berbagai metode perkiraan seperti aturan trapesium, aturan mid-ordinat atau aturan Simpson. Kemudian area matematika di bawah setengah siklus positif dari gelombang periodik yang didefinisikan sebagai V(t) = Vp.cos (ωt) dengan periode T menggunakan integrasi diberikan sebagai:
Area = ∫0π VP sin (ωt) dt
Di mana: 0 dan π adalah batas integrasi karena kami menentukan nilai rata-rata tegangan lebih dari setengah siklus. Kemudian area di bawah kurva akhirnya diberikan sebagai Area = 2VP.
Karena kita sekarang mengetahui daerah di bawah setengah siklus positif (atau negatif), kita dapat dengan mudah menentukan nilai rata-rata area positif (atau negatif) dari bentuk gelombang sinusoidal dengan mengintegrasikan kuantitas sinusoidal lebih dari setengah siklus dan membaginya dengan setengah periode .
Sebagai contoh, jika tegangan sesaat dari sinusoidal diberikan sebagai: v = Vp.sinθ dan periode sinusoidal diberikan sebagai: 2π, maka:
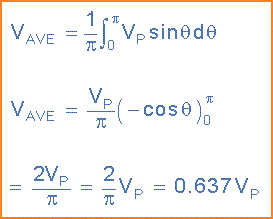
Yang karenanya diberikan sebagai persamaan standar untuk Tegangan Rata-rata dari gelombang sinusoidal sebagai:
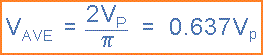
Tegangan rata-rata ( VAV ) dari gelombang sinusoidal ditentukan dengan mengalikan nilai tegangan puncak dengan konstanta 0.637, yang dua dibagi dengan pi ( π ). Tegangan rata-rata, yang juga dapat disebut sebagai nilai rata-rata, tergantung pada besarnya gelombang dan bukan merupakan fungsi dari frekuensi atau sudut fase.
Dengan demikian nilai rata-rata atau mean ini (baik tegangan atau arus) dari bentuk gelombang sinusoidal juga dapat ditampilkan sebagai nilai DC setara/ekuivalen dari area dan waktu.
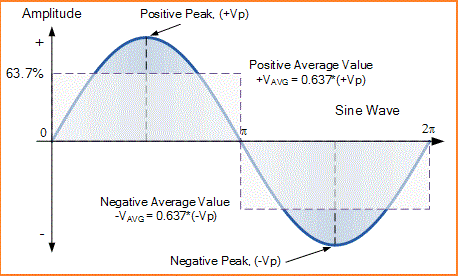
Nilai rata-rata adalah nol selama satu siklus lengkap, karena area rata-rata positif akan dibatalkan oleh area rata-rata negatif (VAVG - (-VAVG)) dalam jumlah kedua area, sehingga menghasilkan tegangan rata-rata nol pada satu siklus lengkap siklus sinusoidal.
Mengacu pada contoh grafis kami di atas, tegangan puncak, (Vpk) diberikan sebagai 20 Volt. Dengan menggunakan metode analitik, tegangan rata-rata dihitung sebagai:
VAV = Vpk x 0,637 = 20 x 0,637 = 12,74 volt
Yang merupakan nilai yang sama dengan metode grafis.
Untuk menemukan nilai puncak dari nilai tegangan rata-rata yang diberikan, cukup atur ulang rumus dan bagi dengan konstanta. Misalnya, berapa nilai puncak sinusoidal, Vpk jika nilai rata-rata adalah 65 volt.
Vpk = VAV ÷ 0,637 = 65 ÷ 0,637 = 102 volt
Perhatikan bahwa mengalikan nilai puncak atau maksimum dengan konstanta 0.637 HANYA berlaku untuk bentuk gelombang sinusoidal.
Nilai rata-rata dari gelombang sinusoidal tegangan atau arus adalah 0,637 kali nilai puncak, ( Vp atau Ip). Hubungan matematis antara nilai rata-rata ini berlaku untuk arus AC dan tegangan AC.
Kadang-kadang diperlukan untuk dapat menghitung nilai tegangan langsung atau arus keluaran dari rangkaian penyearah atau jenis pulsa seperti rangkaian motor PWM karena tegangan atau arus, meskipun tidak terbalik, berubah terus menerus. Karena tidak ada pembalikan fase, nilai rata-rata digunakan dan nilai RMS (root-mean-square) tidak penting untuk jenis aplikasi ini.
Perbedaan utama antara Tegangan RMS dan Tegangan Rata-rata adalah bahwa nilai rata-rata dari gelombang periodik adalah rata-rata dari semua area sesaat yang diambil di bawah kurva selama periode gelombang tertentu, dan dalam kasus kuantitas sinusoidal, periode ini diambil sebagai setengah dari siklus gelombang. Untuk kenyamanan, setengah siklus positif umumnya digunakan.
Nilai efektif atau nilai akar-rata-kuadrat (RMS) dari bentuk gelombang adalah nilai panas efektif gelombang dibandingkan dengan nilai DC stabil dan merupakan akar kuadrat dari rata-rata kuadrat dari nilai sesaat yang diambil dari satu siklus lengkap .
Untuk HANYA bentuk gelombang sinusoidal murni, baik tegangan rata-rata dan tegangan RMS (atau arus) dapat dengan mudah dihitung sebagai:
Nilai rata-rata = 0.637 × nilai maksimum atau puncak, Vpk
Nilai RMS = 0.707 × nilai maksimum atau puncak, Vpk

Satu komentar terakhir tentang penggunaan Tegangan Rata - rata dan Tegangan RMS. Kedua nilai dapat digunakan untuk mewakili "Faktor Bentuk" dari gelombang bolak-balik sinusoidal. Faktor bentuk didefinisikan sebagai bentuk gelombang AC dan merupakan tegangan RMS dibagi dengan tegangan rata-rata (faktor bentuk = nilai rms/nilai rata-rata).
Jadi untuk bentuk gelombang sinusoidal atau kompleks faktor bentuk diberikan sebagai: ( π / (2√2) ) yang kira-kira sama dengan konstanta, 1.11. Faktor bentuk adalah rasio dan karenanya tidak memiliki unit listrik. Jika faktor bentuk gelombang sinusoidal diketahui, maka tegangan rata-rata dapat ditemukan menggunakan nilai tegangan RMS dan sebaliknya karena tegangan rata-rata adalah 0.9 kali nilai tegangan RMS dari gelombang sinusoidal.
Dalam tutorial ini kita akan belajar menghitung "rata-rata" atau nilai tegangan rata-rata dari bentuk gelombang sinusoidal menggunakan rumus mid-ordinat dan rumus analitik. Proses yang digunakan untuk menemukan Tegangan Rata-rata dari gelombang bolak-balik sangat mirip dengan yang untuk menemukan nilai RMS-nya, perbedaan kali ini adalah bahwa nilai sesaat tidak kuadrat dan kami tidak menemukan akar kuadrat dari rangkuman rata-rata.
Tegangan atau Arus rata-rata dari suatu gelombang periodik apakah itu gelombang sinusoidal, gelombang persegi atau gelombang segitiga didefinisikan sebagai: "hasil bagi dari daerah di bawah bentuk gelombang sehubungan dengan waktu". Dengan kata lain, rata-rata semua nilai sesaat sepanjang sumbu waktu dengan waktu menjadi satu periode penuh, ( T ).
Untuk bentuk gelombang periodik, area di atas sumbu horizontal positif sedangkan area di bawah sumbu horizontal negatif. Hasilnya adalah bahwa nilai rata-rata atau rata-rata kuantitas bolak-balik simetris adalah nol, (0) karena area di atas sumbu horizontal (setengah siklus positif) sama dengan area di bawah sumbu (setengah siklus negatif) dan dengan demikian membatalkan satu sama lain.
Ini karena ketika kita melakukan perhitungan matematika dari dua area, area negatif membatalkan area positif yang menghasilkan tegangan rata-rata nol. Maka nilai rata-rata atau rata-rata dari kuantitas bolak-balik simetris, seperti gelombang sinusoidal, adalah nilai rata-rata yang diukur hanya setengah dari siklus, karena seperti yang baru saja kami nyatakan, nilai rata-rata selama satu siklus lengkap adalah nol terlepas dari amplitudo puncak.
Istilah dalam kelistrikan Tegangan rata-rata atau Arus rata-rata, dapat digunakan dalam analisis atau perhitungan rangkaian AC dan DC. Simbol yang digunakan untuk mewakili nilai rata-rata didefinisikan sebagai: VAV atau IAV.
Metode Grafis Tegangan Rata-rata
Sekali lagi pertimbangkan hanya setengah siklus positif dari tutorial tegangan RMS sebelumnya. Tegangan rata-rata atau mean dari suatu gelombang dapat ditemukan lagi dengan jumlah akurasi yang masuk akal dengan mengambil nilai-nilai sesaat spasi yang sama.Setengah positif dari gelombang dibagi menjadi sejumlah "n" bagian yang sama atau pertengahan-ordinat. Lebar setiap pertengahan-ordinat akan menjadi n° derajat (atau t detik) dan tinggi setiap pertengahan-ordinat akan sama dengan nilai sesaat dari bentuk gelombang pada titik itu sepanjang sumbu x dari bentuk gelombang.
Metode Grafis

Setiap nilai pertengahan-ordinat dari bentuk gelombang tegangan ditambahkan ke depan dan total dijumlahkan, V1 ke V12 dibagi dengan jumlah mid-kordinat digunakan untuk memberi kita “ Tegangan rata-rata”. Kemudian tegangan rata-rata (VAV) adalah jumlah rata-rata dari pertengahan-ordinat dari gelombang tegangan dan diberikan sebagai:

dan untuk contoh sederhana kami di atas, tegangan rata-rata karena itu dihitung sebagai:

Jadi seperti sebelumnya mari kita asumsikan lagi bahwa tegangan bolak-balik 20 volt puncak bervariasi selama satu setengah siklus sebagai berikut:
Tegangan
|
6.2V
|
11.8V
|
16.2V
|
19.0V
|
20.0V
|
19.0V
|
16.2V
|
11.8V
|
6.2V
|
0V
|
Sudut
|
18°
|
36°
|
54°
|
72°
|
90°
|
108°
|
126°
|
144°
|
162°
|
180°
|
Nilai tegangan rata - rata karena itu dihitung sebagai:

Kemudian nilai Tegangan rata-rata untuk satu setengah siklus menggunakan metode grafis diberikan sebagai: 12,64 Volts .
Metode Analisis Tegangan Rata-Rata
Seperti yang dikatakan sebelumnya, tegangan rata-rata bentuk gelombang periodik yang dua bagiannya persis sama, baik sinusoidal atau non-sinusoidal, akan menjadi nol selama satu siklus lengkap. Kemudian nilai rata-rata diperoleh dengan menambahkan nilai tegangan sesaat hanya pada setengah siklus saja. Tetapi dalam kasus gelombang non-simetris atau kompleks, tegangan rata-rata (atau arus) harus diambil alih seluruh siklus periodik secara matematis.Nilai rata-rata dapat diambil secara matematis dengan mengambil perkiraan area di bawah kurva pada berbagai interval dengan jarak atau panjang pangkalan dan ini dapat dilakukan dengan menggunakan segitiga atau persegi panjang seperti yang ditunjukkan.
Perkiraan Area

Dengan mendekati area persegi panjang di bawah kurva, kita dapat memperoleh gambaran kasar dari area aktual masing-masing. Dengan menambahkan bersama semua bidang ini, nilai rata-rata dapat ditemukan. Jika jumlah tak terbatas dari persegi panjang tipis yang lebih kecil digunakan, yang lebih akurat akan menjadi hasil akhir saat mendekati 2/π.
Area di bawah kurva dapat ditemukan dengan berbagai metode perkiraan seperti aturan trapesium, aturan mid-ordinat atau aturan Simpson. Kemudian area matematika di bawah setengah siklus positif dari gelombang periodik yang didefinisikan sebagai V(t) = Vp.cos (ωt) dengan periode T menggunakan integrasi diberikan sebagai:
Area = ∫0π VP sin (ωt) dt
Di mana: 0 dan π adalah batas integrasi karena kami menentukan nilai rata-rata tegangan lebih dari setengah siklus. Kemudian area di bawah kurva akhirnya diberikan sebagai Area = 2VP.
Karena kita sekarang mengetahui daerah di bawah setengah siklus positif (atau negatif), kita dapat dengan mudah menentukan nilai rata-rata area positif (atau negatif) dari bentuk gelombang sinusoidal dengan mengintegrasikan kuantitas sinusoidal lebih dari setengah siklus dan membaginya dengan setengah periode .
Sebagai contoh, jika tegangan sesaat dari sinusoidal diberikan sebagai: v = Vp.sinθ dan periode sinusoidal diberikan sebagai: 2π, maka:
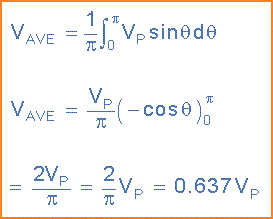
Yang karenanya diberikan sebagai persamaan standar untuk Tegangan Rata-rata dari gelombang sinusoidal sebagai:
Persamaan Tegangan Rata-rata
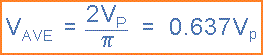
Tegangan rata-rata ( VAV ) dari gelombang sinusoidal ditentukan dengan mengalikan nilai tegangan puncak dengan konstanta 0.637, yang dua dibagi dengan pi ( π ). Tegangan rata-rata, yang juga dapat disebut sebagai nilai rata-rata, tergantung pada besarnya gelombang dan bukan merupakan fungsi dari frekuensi atau sudut fase.
Dengan demikian nilai rata-rata atau mean ini (baik tegangan atau arus) dari bentuk gelombang sinusoidal juga dapat ditampilkan sebagai nilai DC setara/ekuivalen dari area dan waktu.

Nilai rata-rata adalah nol selama satu siklus lengkap, karena area rata-rata positif akan dibatalkan oleh area rata-rata negatif (VAVG - (-VAVG)) dalam jumlah kedua area, sehingga menghasilkan tegangan rata-rata nol pada satu siklus lengkap siklus sinusoidal.
Mengacu pada contoh grafis kami di atas, tegangan puncak, (Vpk) diberikan sebagai 20 Volt. Dengan menggunakan metode analitik, tegangan rata-rata dihitung sebagai:
VAV = Vpk x 0,637 = 20 x 0,637 = 12,74 volt
Yang merupakan nilai yang sama dengan metode grafis.
Untuk menemukan nilai puncak dari nilai tegangan rata-rata yang diberikan, cukup atur ulang rumus dan bagi dengan konstanta. Misalnya, berapa nilai puncak sinusoidal, Vpk jika nilai rata-rata adalah 65 volt.
Vpk = VAV ÷ 0,637 = 65 ÷ 0,637 = 102 volt
Perhatikan bahwa mengalikan nilai puncak atau maksimum dengan konstanta 0.637 HANYA berlaku untuk bentuk gelombang sinusoidal.
Ringkasan Tegangan Rata-rata
Nilai rata-rata dari seluruh bentuk gelombang sinusoidal selama satu siklus lengkap adalah nol karena kedua bagian saling membatalkan, sehingga nilai rata-rata diambil lebih dari setengah siklus.Nilai rata-rata dari gelombang sinusoidal tegangan atau arus adalah 0,637 kali nilai puncak, ( Vp atau Ip). Hubungan matematis antara nilai rata-rata ini berlaku untuk arus AC dan tegangan AC.
Kadang-kadang diperlukan untuk dapat menghitung nilai tegangan langsung atau arus keluaran dari rangkaian penyearah atau jenis pulsa seperti rangkaian motor PWM karena tegangan atau arus, meskipun tidak terbalik, berubah terus menerus. Karena tidak ada pembalikan fase, nilai rata-rata digunakan dan nilai RMS (root-mean-square) tidak penting untuk jenis aplikasi ini.
Perbedaan utama antara Tegangan RMS dan Tegangan Rata-rata adalah bahwa nilai rata-rata dari gelombang periodik adalah rata-rata dari semua area sesaat yang diambil di bawah kurva selama periode gelombang tertentu, dan dalam kasus kuantitas sinusoidal, periode ini diambil sebagai setengah dari siklus gelombang. Untuk kenyamanan, setengah siklus positif umumnya digunakan.
Nilai efektif atau nilai akar-rata-kuadrat (RMS) dari bentuk gelombang adalah nilai panas efektif gelombang dibandingkan dengan nilai DC stabil dan merupakan akar kuadrat dari rata-rata kuadrat dari nilai sesaat yang diambil dari satu siklus lengkap .
Untuk HANYA bentuk gelombang sinusoidal murni, baik tegangan rata-rata dan tegangan RMS (atau arus) dapat dengan mudah dihitung sebagai:
Nilai rata-rata = 0.637 × nilai maksimum atau puncak, Vpk
Nilai RMS = 0.707 × nilai maksimum atau puncak, Vpk

Satu komentar terakhir tentang penggunaan Tegangan Rata - rata dan Tegangan RMS. Kedua nilai dapat digunakan untuk mewakili "Faktor Bentuk" dari gelombang bolak-balik sinusoidal. Faktor bentuk didefinisikan sebagai bentuk gelombang AC dan merupakan tegangan RMS dibagi dengan tegangan rata-rata (faktor bentuk = nilai rms/nilai rata-rata).
Jadi untuk bentuk gelombang sinusoidal atau kompleks faktor bentuk diberikan sebagai: ( π / (2√2) ) yang kira-kira sama dengan konstanta, 1.11. Faktor bentuk adalah rasio dan karenanya tidak memiliki unit listrik. Jika faktor bentuk gelombang sinusoidal diketahui, maka tegangan rata-rata dapat ditemukan menggunakan nilai tegangan RMS dan sebaliknya karena tegangan rata-rata adalah 0.9 kali nilai tegangan RMS dari gelombang sinusoidal.