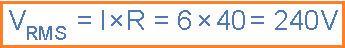Rangkaian AC dan Gelombang AC
Gelombang Sinus AC dibuat dengan memutar kumparan di dalam medan magnet dan tegangan dan arus bolak-balik membentuk dasar dari Teori AC.
Istilah AC atau Alternating Current, umumnya mengacu pada bentuk gelombang yang bervariasi waktu dengan yang paling umum disebut Sinusoid atau lebih dikenal sebagai Gelombang Sinusoidal. Bentuk gelombang sinusoidal umumnya disebut dengan deskripsi singkat mereka sebagai Gelombang Sinus. Gelombang sinus adalah salah satu tipe gelombang AC yang paling penting yang digunakan dalam teknik elektro.
Bentuk yang diperoleh dengan memplotkan nilai ordinat/tengah dari tegangan atau arus terhadap waktu disebut Gelombang AC. Bentuk gelombang AC terus-menerus mengubah polaritasnya setiap setengah siklus bergantian antara nilai maksimum positif dan nilai maksimum negatif, masing-masing berkaitan dengan waktu. Contoh umum dari hal ini adalah supply tegangan utama rumah tangga yang kita gunakan di rumah kita.
Ini berarti bahwa bentuk gelombang AC adalah "sinyal tergantung waktu" dengan tipe sinyal waktu yang paling umum bergantung dari bentuk gelombang Periodik. Bentuk gelombang AC atau Periodik adalah hasil yang dihasilkan dari perputaran generator listrik. Umumnya, bentuk-bentuk gelombang periodik dapat dihasilkan dengan menggunakan frekuensi dasar dan melapiskannya dengan sinyal harmonik dari frekuensi dan amplitudo yang berbeda-beda.
Tegangan dan arus bolak-balik tidak dapat disimpan dalam baterai atau sel-sel seperti arus searah (DC), itu jauh lebih mudah dan murah untuk menghasilkan jumlah ini dengan menggunakan alternator atau generator gelombang saat dibutuhkan.
Tipe dan bentuk bentuk gelombang AC bergantung pada generator atau perangkat yang memproduksinya, namun semua bentuk gelombang AC terdiri dari garis tegangan nol yang membagi bentuk gelombang menjadi dua bagian simetris.
Karakteristik utama dari bentuk Gelombang AC didefinisikan sebagai:
Umumnya, untuk bentuk gelombang AC, garis dasar horizontal ini mewakili kondisi nol dari tegangan atau arus. Setiap bagian dari bentuk gelombang jenis AC yang berada di atas sumbu nol horizontal mewakili tegangan atau arus yang mengalir dalam satu arah.
Demikian juga, bagian dari bentuk gelombang yang berada di bawah sumbu nol horizontal mewakili tegangan atau arus yang mengalir ke arah yang berlawanan dengan yang pertama. Umumnya untuk sinusoidal bentuk gelombang AC dari bentuk gelombang di atas sumbu nol adalah sama dengan bentuk di bawah ini. Namun, untuk sebagian besar sinyal non-daya AC termasuk bentuk gelombang audio, hal ini tidak selalu terjadi.
Bentuk gelombang sinyal periodik yang paling umum yang digunakan dalam Teknik Elektronik dan Listrik adalah bentuk Gelombang Sinusoidal. Namun, bentuk gelombang AC bolak-balik mungkin tidak selalu berbentuk merata yang didasarkan pada fungsi trigonometri sinus atau cosinus.
Bentuk gelombang AC juga bisa berbentuk Gelombang Kompleks, Gelombang Persegi atau Gelombang Segitiga dan ini ditunjukkan di bawah ini.

Waktu yang dibutuhkan untuk membentuk Gelombang AC untuk melengkapi satu pola penuh dari setengah positifnya ke setengah negatifnya dan kembali ke garis dasar nolnya lagi disebut Siklus dan satu siklus lengkap berisi siklus setengah positif dan setengah siklus negatif. Kemudian waktu yang dibutuhkan oleh bentuk gelombang untuk menyelesaikan satu siklus penuh disebut Waktu Periodik dari bentuk gelombang, dan diberi simbol "T" .
Jumlah siklus lengkap yang dihasilkan dalam satu detik (siklus/detik) disebut Frekuensi, simbol ƒ dari bentuk gelombang bolak-balik. Frekuensi diukur dalam Hertz, (Hz) dinamai menurut fisikawan Jerman Heinrich Hertz.
Kemudian kita dapat melihat bahwa ada hubungan antara siklus (osilasi), waktu dan frekuensi periodik (siklus per detik), jadi jika ada ƒ jumlah siklus dalam satu detik, setiap siklus individu harus mengambil 1/ƒ detik untuk menyelesaikannya.
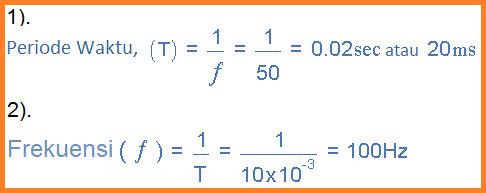
Frekuensi yang digunakan untuk dinyatakan dalam "siklus per detik" disingkat menjadi "cps/cycle per second", tapi saat ini lebih umum ditentukan dalam unit yang disebut "Hertz". Untuk supply listrik domestik, frekuensi 50Hz atau 60Hz tergantung pada negara dan dengan kecepatan rotasi generator.
Tapi satu hertz adalah unit yang sangat kecil sehingga digunakan satuan berbeda yang menunjukkan urutan besarnya bentuk gelombang pada frekuensi yang lebih tinggi seperti kHz , MHz dan bahkan GHz.
Nilai puncak adalah nilai terbesar dari tegangan atau arus yang dicapai gelombang setiap setengah siklus yang diukur dari garis dasar nol. Tidak seperti tegangan DC atau arus yang memiliki keadaan mapan yang dapat diukur atau dihitung dengan menggunakan Hukum Ohm, kuantitas bergantian terus berubah nilainya dari waktu ke waktu.
Untuk bentuk gelombang sinusoidal murni, nilai puncak ini akan selalu sama untuk kedua siklus setengah ( +Vm = -Vm ), tetapi untuk bentuk gelombang non-sinusoidal atau kompleks, nilai puncak maksimum bisa sangat berbeda untuk setiap setengah siklus.
Terkadang, bentuk gelombang bolak-balik dari puncak-ke-puncak, nilai Vp-p dan ini adalah jarak atau jumlah tegangan antara nilai puncak maksimum, + Vmax dan nilai puncak minimum, -Vmax selama satu siklus lengkap.
Dalam gelombang sinus murni jika nilai rata-rata dihitung selama siklus penuh, nilai rata-rata akan sama dengan nol karena bagian positif dan negatif akan saling membatalkan. Jadi nilai rata-rata atau mean dari bentuk gelombang AC dihitung atau diukur lebih dari setengah siklus saja dan ini ditunjukkan di bawah ini.
Untuk mencari nilai rata-rata dari bentuk gelombang yang kita butuhkan untuk menghitung area di bawah bentuk gelombang menggunakan aturan mid-ordinat, aturan trapesium atau aturan Simpson yang umum digunakan dalam matematika.
Area perkiraan di bawah bentuk gelombang tidak teratur dapat dengan mudah ditemukan dengan hanya menggunakan rumus mid-ordinat. Garis dasar sumbu nol dibagi menjadi beberapa bagian yang sama dan pada contoh sederhana di atas nilai ini adalah sembilan, (V1 sampai V9).
Semakin banyak garis ordinat yang digambar semakin akurat akan menjadi rata-rata akhir atau nilai rata-rata. Nilai rata-rata adalah penambahan semua nilai seketika yang ditambah bersama-sama dan kemudian dibagi dengan jumlah total. Contohnya berikut ini.
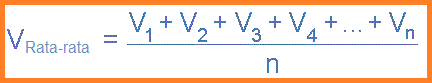
Dimana: n sama dengan jumlah sebenarnya dari mid-ordinat yang digunakan.
Untuk bentuk gelombang sinusoidal murni nilai rata-rata ini akan selalu sama dengan 0,637*Vmax dan hubungan ini juga berlaku untuk nilai rata-rata arus.
Dengan demikian nilai ekuivalen untuk sistem arus bolak-balik yang menyediakan jumlah daya listrik yang sama ke beban seperti rangkaian ekuivalen DC disebut "nilai efektif". Nilai efektif gelombang sinus menghasilkan efek pemanasan I2*R yang sama dalam beban seperti yang kita harapkan untuk melihat apakah beban yang sama diumpankan oleh supply DC yang konstan.
Nilai efektif dari gelombang sinus lebih dikenal sebagai Root Mean Squared atau hanya nilai RMS karena dihitung sebagai akar kuadrat dari rata-rata (mean) kuadrat dari tegangan atau arus. Yaitu Vrms atau Irms diberikan sebagai akar kuadrat dari rata-rata jumlah semua nilai tengah-ordinat kuadrat dari gelombang sinus.
Nilai RMS untuk setiap bentuk gelombang AC dapat ditemukan dari rumus nilai rata-rata yang dimodifikasi berikut ini seperti yang ditunjukkan.
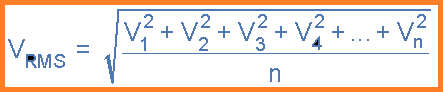
Dimana: n sama dengan jumlah mid-ordinat.
Untuk bentuk gelombang sinusoidal murni nilai efektif atau R.M.S ini akan selalu sama dengan 1/√2*Vmax yang sama dengan 0,707*Vmax dan hubungan juga ini berlaku untuk nilai RMS arus.
Nilai RMS untuk bentuk gelombang sinusoidal selalu lebih besar dari nilai rata-rata kecuali untuk bentuk gelombang persegi panjang. Dalam hal ini efek pemanasan tetap konstan sehingga rata-rata dan nilai RMS akan sama.
Satu komentar terakhir tentang nilai R.M.S. Sebagian besar alat ukur listrik multimeter, baik digital maupun analog hanya mengukur nilai R.M.S tegangan dan arus dan bukan rata-rata. Oleh karena itu ketika menggunakan multimeter pada sistem arus searah bacaan akan sama dengan I=V/R dan untuk sistem arus bolak-balik bacaan akan sama dengan Irms = Vrms/R.
Selain itu, kecuali untuk perhitungan daya rata-rata, saat menghitung RMS atau tegangan puncak, hanya gunakan VRMS untuk menemukan nilai IRMS, atau tegangan puncak, Vp untuk menemukan arus puncak, nilai Ip. Jangan gabungkan keduanya karena nilai Average, RMS atau Peak dari gelombang sinus benar-benar berbeda dan hasil Anda pasti salah.

Untuk bentuk gelombang sinusoidal murni, Faktor bentuk akan selalu sama dengan 1,11. Faktor Puncak adalah rasio antara nilai R.M.S dan nilai Puncak dari bentuk gelombang dan dirumuskan sebagai.

Untuk bentuk gelombang sinusoidal murni, Faktor Puncak akan selalu sama dengan 1,414.
Nilai Tegangan R.M.S. dirumuskan sebagai:
Nilai Tegangan Rata-rata dirumuskan sebagai:

Nilai Tegangan Puncak dirumuskan sebagai:
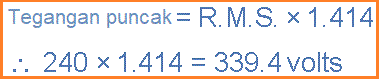
Penggunaan dan perhitungan Rata-rata, R.M.S, Faktor Bentuk dan Faktor Puncak juga dapat digunakan dengan semua jenis bentuk gelombang periodik termasuk Segitiga, Persegi, Bergigi atau bentuk gelombang arus / tegangan tidak teratur atau kompleks lainnya. Konversi antara berbagai nilai sinusoidal terkadang membingungkan sehingga tabel berikut memberi cara mudah untuk mengubah satu nilai gelombang sinus ke yang lainnya.
Pada tutorial berikutnya tentang bentuk Gelombang Sinusoidal kita akan belajar pokok utama bentuk gelombang sinusoidal AC (sinusoid) bersamaan dengan representasi kecepatan sudutnya.
Rangkaian dan Gelombang AC
Fungsi arus bolak-balik atau bentuk Gelombang AC di sisi lain didefinisikan sebagai salah satu yang bervariasi baik dalam besaran maupun arahnya dalam waktu kurang lebih satu arah dengan waktu sehingga membentuk gelombang "Bi-directional/Dua-arah". Fungsi AC dapat mewakili sumber daya atau sumber sinyal dengan bentuk gelombang AC umumnya mengikuti sinusoid matematis seperti yang didefinisikan oleh: A(t) = Amax *sin (2πƒt) .Istilah AC atau Alternating Current, umumnya mengacu pada bentuk gelombang yang bervariasi waktu dengan yang paling umum disebut Sinusoid atau lebih dikenal sebagai Gelombang Sinusoidal. Bentuk gelombang sinusoidal umumnya disebut dengan deskripsi singkat mereka sebagai Gelombang Sinus. Gelombang sinus adalah salah satu tipe gelombang AC yang paling penting yang digunakan dalam teknik elektro.
Bentuk yang diperoleh dengan memplotkan nilai ordinat/tengah dari tegangan atau arus terhadap waktu disebut Gelombang AC. Bentuk gelombang AC terus-menerus mengubah polaritasnya setiap setengah siklus bergantian antara nilai maksimum positif dan nilai maksimum negatif, masing-masing berkaitan dengan waktu. Contoh umum dari hal ini adalah supply tegangan utama rumah tangga yang kita gunakan di rumah kita.
Ini berarti bahwa bentuk gelombang AC adalah "sinyal tergantung waktu" dengan tipe sinyal waktu yang paling umum bergantung dari bentuk gelombang Periodik. Bentuk gelombang AC atau Periodik adalah hasil yang dihasilkan dari perputaran generator listrik. Umumnya, bentuk-bentuk gelombang periodik dapat dihasilkan dengan menggunakan frekuensi dasar dan melapiskannya dengan sinyal harmonik dari frekuensi dan amplitudo yang berbeda-beda.
Tegangan dan arus bolak-balik tidak dapat disimpan dalam baterai atau sel-sel seperti arus searah (DC), itu jauh lebih mudah dan murah untuk menghasilkan jumlah ini dengan menggunakan alternator atau generator gelombang saat dibutuhkan.
Tipe dan bentuk bentuk gelombang AC bergantung pada generator atau perangkat yang memproduksinya, namun semua bentuk gelombang AC terdiri dari garis tegangan nol yang membagi bentuk gelombang menjadi dua bagian simetris.
Karakteristik utama dari bentuk Gelombang AC didefinisikan sebagai:
Karakteristik Gelombang AC
- Periode/Waktu, (T) adalah panjang waktu dalam hitungan detik yang bentuk gelombangnya mengulang dari awal sampai akhir. Ini juga bisa disebut Waktu perodik/berkala dari bentuk gelombang untuk gelombang sinus, atau lebar Pulse untuk gelombang persegi.
- Frekuensi, (ƒ) adalah berapa kali bentuk gelombang berulang dalam waktu satu periode kedua. Frekuensi adalah kebalikan dari periode waktu, ( ƒ = 1/T ) dengan satuan frekuensi menjadi Hertz, (Hz).
- Amplitudo (A) adalah besarnya atau intensitas bentuk gelombang sinyal yang diukur dalam volt atau ampere.
Umumnya, untuk bentuk gelombang AC, garis dasar horizontal ini mewakili kondisi nol dari tegangan atau arus. Setiap bagian dari bentuk gelombang jenis AC yang berada di atas sumbu nol horizontal mewakili tegangan atau arus yang mengalir dalam satu arah.
Demikian juga, bagian dari bentuk gelombang yang berada di bawah sumbu nol horizontal mewakili tegangan atau arus yang mengalir ke arah yang berlawanan dengan yang pertama. Umumnya untuk sinusoidal bentuk gelombang AC dari bentuk gelombang di atas sumbu nol adalah sama dengan bentuk di bawah ini. Namun, untuk sebagian besar sinyal non-daya AC termasuk bentuk gelombang audio, hal ini tidak selalu terjadi.
Bentuk gelombang sinyal periodik yang paling umum yang digunakan dalam Teknik Elektronik dan Listrik adalah bentuk Gelombang Sinusoidal. Namun, bentuk gelombang AC bolak-balik mungkin tidak selalu berbentuk merata yang didasarkan pada fungsi trigonometri sinus atau cosinus.
Bentuk gelombang AC juga bisa berbentuk Gelombang Kompleks, Gelombang Persegi atau Gelombang Segitiga dan ini ditunjukkan di bawah ini.
Jenis (tipe) Gelombang Periodik

Waktu yang dibutuhkan untuk membentuk Gelombang AC untuk melengkapi satu pola penuh dari setengah positifnya ke setengah negatifnya dan kembali ke garis dasar nolnya lagi disebut Siklus dan satu siklus lengkap berisi siklus setengah positif dan setengah siklus negatif. Kemudian waktu yang dibutuhkan oleh bentuk gelombang untuk menyelesaikan satu siklus penuh disebut Waktu Periodik dari bentuk gelombang, dan diberi simbol "T" .
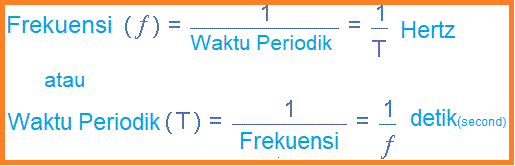
Jumlah siklus lengkap yang dihasilkan dalam satu detik (siklus/detik) disebut Frekuensi, simbol ƒ dari bentuk gelombang bolak-balik. Frekuensi diukur dalam Hertz, (Hz) dinamai menurut fisikawan Jerman Heinrich Hertz.
Kemudian kita dapat melihat bahwa ada hubungan antara siklus (osilasi), waktu dan frekuensi periodik (siklus per detik), jadi jika ada ƒ jumlah siklus dalam satu detik, setiap siklus individu harus mengambil 1/ƒ detik untuk menyelesaikannya.
Hubungan Antara Frekuensi dan Waktu Periodik

Contoh: Gelombang AC No.1
- Berapa waktu periodik dari bentuk gelombang 50Hz dan
- Berapakah frekuensi gelombang AC yang memiliki waktu periodik 10mS.
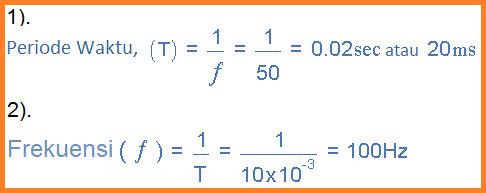
Frekuensi yang digunakan untuk dinyatakan dalam "siklus per detik" disingkat menjadi "cps/cycle per second", tapi saat ini lebih umum ditentukan dalam unit yang disebut "Hertz". Untuk supply listrik domestik, frekuensi 50Hz atau 60Hz tergantung pada negara dan dengan kecepatan rotasi generator.
Tapi satu hertz adalah unit yang sangat kecil sehingga digunakan satuan berbeda yang menunjukkan urutan besarnya bentuk gelombang pada frekuensi yang lebih tinggi seperti kHz , MHz dan bahkan GHz.
Definisi Tabel Satuan Frekuensi
Satuan
|
Definisi
|
Ditulis
|
Waktu periodik
|
Kilo
|
Ribu
|
kHz
|
1ms
|
Mega
|
Juta
|
MHz
|
1us
|
Giga
|
Milyar
|
GHz
|
1ns
|
Terra
|
Triliun
|
THz
|
1ps
|
Amplitudo dari Gelombang AC
Juga mengetahui baik waktu periodik atau frekuensi kuantitas bolak-balik, parameter penting lain dari gelombang AC adalah Amplitudo, atau yang lebih dikenal sebagai nilai maksimum atau Puncak yang diwakili oleh istilah, Vmax untuk tegangan atau Imax untuk arus.Nilai puncak adalah nilai terbesar dari tegangan atau arus yang dicapai gelombang setiap setengah siklus yang diukur dari garis dasar nol. Tidak seperti tegangan DC atau arus yang memiliki keadaan mapan yang dapat diukur atau dihitung dengan menggunakan Hukum Ohm, kuantitas bergantian terus berubah nilainya dari waktu ke waktu.
Untuk bentuk gelombang sinusoidal murni, nilai puncak ini akan selalu sama untuk kedua siklus setengah ( +Vm = -Vm ), tetapi untuk bentuk gelombang non-sinusoidal atau kompleks, nilai puncak maksimum bisa sangat berbeda untuk setiap setengah siklus.
Terkadang, bentuk gelombang bolak-balik dari puncak-ke-puncak, nilai Vp-p dan ini adalah jarak atau jumlah tegangan antara nilai puncak maksimum, + Vmax dan nilai puncak minimum, -Vmax selama satu siklus lengkap.
Nilai rata-rata Gelombang
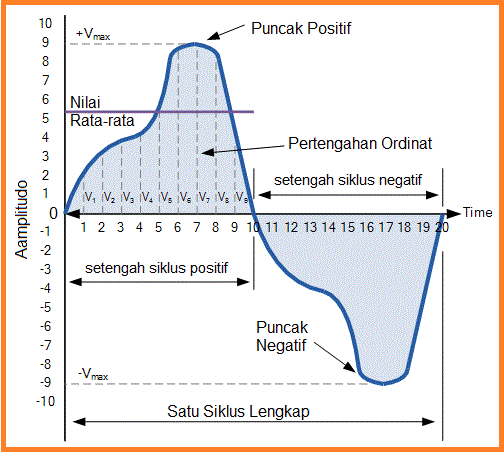
Rata-rata atau Nilai rata-rata dari tegangan DC kontinyu akan selalu sama dengan nilai puncak maksimumnya karena tegangan DC konstan. Nilai rata-rata ini hanya akan berubah jika siklus kerja (duty cycle) dari tegangan DC berubah.Dalam gelombang sinus murni jika nilai rata-rata dihitung selama siklus penuh, nilai rata-rata akan sama dengan nol karena bagian positif dan negatif akan saling membatalkan. Jadi nilai rata-rata atau mean dari bentuk gelombang AC dihitung atau diukur lebih dari setengah siklus saja dan ini ditunjukkan di bawah ini.
Nilai rata-rata Pada Gelombang Non-sinusoidal

Untuk mencari nilai rata-rata dari bentuk gelombang yang kita butuhkan untuk menghitung area di bawah bentuk gelombang menggunakan aturan mid-ordinat, aturan trapesium atau aturan Simpson yang umum digunakan dalam matematika.
Area perkiraan di bawah bentuk gelombang tidak teratur dapat dengan mudah ditemukan dengan hanya menggunakan rumus mid-ordinat. Garis dasar sumbu nol dibagi menjadi beberapa bagian yang sama dan pada contoh sederhana di atas nilai ini adalah sembilan, (V1 sampai V9).
Semakin banyak garis ordinat yang digambar semakin akurat akan menjadi rata-rata akhir atau nilai rata-rata. Nilai rata-rata adalah penambahan semua nilai seketika yang ditambah bersama-sama dan kemudian dibagi dengan jumlah total. Contohnya berikut ini.
Nilai Rata-rata Pada Gelombang AC
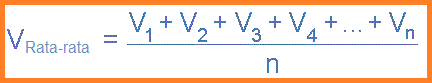
Dimana: n sama dengan jumlah sebenarnya dari mid-ordinat yang digunakan.
Untuk bentuk gelombang sinusoidal murni nilai rata-rata ini akan selalu sama dengan 0,637*Vmax dan hubungan ini juga berlaku untuk nilai rata-rata arus.
Nilai RMS dari Pada Gelombang AC
Nilai rata-rata dari gelombang AC yang kami hitung diatas adalah 0,637*Vmax BUKAN nilai yang sama yang akan kami gunakan untuk supply DC. Ini karena tidak seperti supply DC yang konstan dan dengan nilai tetap, bentuk gelombang AC terus berubah seiring waktu dan tidak memiliki nilai tetap.Dengan demikian nilai ekuivalen untuk sistem arus bolak-balik yang menyediakan jumlah daya listrik yang sama ke beban seperti rangkaian ekuivalen DC disebut "nilai efektif". Nilai efektif gelombang sinus menghasilkan efek pemanasan I2*R yang sama dalam beban seperti yang kita harapkan untuk melihat apakah beban yang sama diumpankan oleh supply DC yang konstan.
Nilai efektif dari gelombang sinus lebih dikenal sebagai Root Mean Squared atau hanya nilai RMS karena dihitung sebagai akar kuadrat dari rata-rata (mean) kuadrat dari tegangan atau arus. Yaitu Vrms atau Irms diberikan sebagai akar kuadrat dari rata-rata jumlah semua nilai tengah-ordinat kuadrat dari gelombang sinus.
Nilai RMS untuk setiap bentuk gelombang AC dapat ditemukan dari rumus nilai rata-rata yang dimodifikasi berikut ini seperti yang ditunjukkan.
Nilai RMS dari Bentuk Gelombang AC
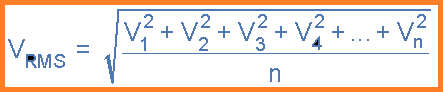
Dimana: n sama dengan jumlah mid-ordinat.
Untuk bentuk gelombang sinusoidal murni nilai efektif atau R.M.S ini akan selalu sama dengan 1/√2*Vmax yang sama dengan 0,707*Vmax dan hubungan juga ini berlaku untuk nilai RMS arus.
Nilai RMS untuk bentuk gelombang sinusoidal selalu lebih besar dari nilai rata-rata kecuali untuk bentuk gelombang persegi panjang. Dalam hal ini efek pemanasan tetap konstan sehingga rata-rata dan nilai RMS akan sama.
Satu komentar terakhir tentang nilai R.M.S. Sebagian besar alat ukur listrik multimeter, baik digital maupun analog hanya mengukur nilai R.M.S tegangan dan arus dan bukan rata-rata. Oleh karena itu ketika menggunakan multimeter pada sistem arus searah bacaan akan sama dengan I=V/R dan untuk sistem arus bolak-balik bacaan akan sama dengan Irms = Vrms/R.
Selain itu, kecuali untuk perhitungan daya rata-rata, saat menghitung RMS atau tegangan puncak, hanya gunakan VRMS untuk menemukan nilai IRMS, atau tegangan puncak, Vp untuk menemukan arus puncak, nilai Ip. Jangan gabungkan keduanya karena nilai Average, RMS atau Peak dari gelombang sinus benar-benar berbeda dan hasil Anda pasti salah.
Faktor Bentuk dan Faktor Puncak
Meskipun sedikit digunakan akhir-akhir ini, baik Faktor Bentuk dan Faktor Puncak dapat digunakan untuk memberi informasi tentang bentuk sebenarnya dari gelombang AC. Faktor bentuk adalah rasio antara nilai rata-rata dan nilai RMS dan dirumuskan sebagai.
Untuk bentuk gelombang sinusoidal murni, Faktor bentuk akan selalu sama dengan 1,11. Faktor Puncak adalah rasio antara nilai R.M.S dan nilai Puncak dari bentuk gelombang dan dirumuskan sebagai.

Untuk bentuk gelombang sinusoidal murni, Faktor Puncak akan selalu sama dengan 1,414.
Contoh: Bentuk Gelombang AC No.2
Arus bolak-balik sinusoidal 6 Amp mengalir melalui hambatan/resistansi 40Ω. Hitung tegangan rata-rata dan tegangan puncak dari supply.Nilai Tegangan R.M.S. dirumuskan sebagai:
Nilai Tegangan Rata-rata dirumuskan sebagai:

Nilai Tegangan Puncak dirumuskan sebagai:
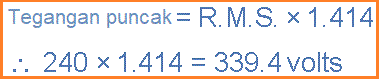
Penggunaan dan perhitungan Rata-rata, R.M.S, Faktor Bentuk dan Faktor Puncak juga dapat digunakan dengan semua jenis bentuk gelombang periodik termasuk Segitiga, Persegi, Bergigi atau bentuk gelombang arus / tegangan tidak teratur atau kompleks lainnya. Konversi antara berbagai nilai sinusoidal terkadang membingungkan sehingga tabel berikut memberi cara mudah untuk mengubah satu nilai gelombang sinus ke yang lainnya.
Tabel Konversi Gelombang Sinusoidal
Konversi dari
|
Kalikan dengan
|
Atau dengan
|
Nilai hasil
|
Puncak
|
2
|
(√2)2
|
Puncak-puncak
|
Puncak ke puncak
|
0.5
|
½
|
Puncak
|
Puncak
|
0.707
|
1/(√2)
|
RMS
|
Puncak
|
0.637
|
2/π
|
Rata-rata
|
Rata-rata
|
1.570
|
π/2
|
Puncak
|
Rata-rata
|
1.111
|
π/(2√2)
|
RMS
|
RMS
|
1.141
|
√2
|
Puncak
|
RMS
|
0.901
|
(2√2)/ π
|
Rata-rata
|