Daya Listrik (Electric Power) pada Rangkaian AC
Daya listrik yang dikonsumsi oleh hambatan/resistansi dalam rangkaian AC berbeda dengan daya yang dikonsumsi oleh reaktansi karena reaktansi tidak menghilangkan energi.
Dalam rangkaian DC, daya yang dikonsumsi hanyalah hasil dari tegangan DC kali arus DC, diberikan dalam watt. Namun, untuk rangkaian AC dengan komponen reaktif kita harus menghitung daya yang dikonsumsi secara berbeda.
Daya listrik adalah "kecepatan" di mana energi dikonsumsi dalam suatu rangkaian dan dengan demikian semua komponen dan perangkat listrik dan elektronik memiliki batas jumlah daya listrik yang dapat mereka tangani dengan aman. Misalnya, resistor 1/4 watt atau amplifier 20 watt.
Daya listrik dapat beragam waktu baik sebagai kuantitas DC atau sebagai kuantitas AC. Jumlah daya dalam suatu rangkaian pada saat kapan saja disebut daya sesaat dan diberikan oleh hubungan daya yang terkenal (P = V*I). Jadi satu watt (yang merupakan tingkat pengeluaran energi pada satu joule per detik) akan sama dengan hasil volt-ampere satu volt kali satu ampere.
Kemudian daya yang diserap atau disuplai oleh elemen rangkaian adalah hasil dari tegangan, V melintasi elemen, dan arus, I mengalir melaluinya. Jadi jika kita memiliki rangkaian DC dengan resistansi "R" ohm, daya yang dihamburkan oleh resistor dalam watt diberikan oleh salah satu rumus umum berikut:

Di mana: V adalah tegangan DC, I adalah arus dc dan R adalah nilai resistansi.
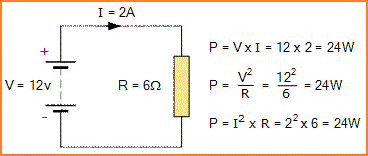
Jadi daya dalam rangkaian listrik hanya ada ketika tegangan dan arus ada, yang tidak ada kondisi rangkaian terbuka atau rangkaian tertutup. Pertimbangkan contoh sederhana berikut dari rangkaian DC resistif standar:
Jadi kita tidak dapat menghitung daya di rangkaian AC dengan cara yang sama seperti di rangkaian DC, tetapi kita masih bisa mengatakan bahwa daya (p) sama dengan tegangan (v) dikalikan dengan arus (i).
Poin penting lainnya adalah bahwa rangkaian AC mengandung reaktansi, sehingga ada komponen daya sebagai hasil dari medan magnet dan/atau listrik yang dibuat oleh komponen.
Hasilnya adalah bahwa tidak seperti komponen resistif murni, daya ini disimpan dan kemudian dikembalikan ke supply ketika gelombang sinusoidal melewati satu siklus periodik lengkap. Dengan demikian, daya rata-rata yang diserap oleh suatu rangkaian adalah jumlah daya yang disimpan dan daya yang dikembalikan selama satu siklus lengkap.
Jadi konsumsi daya rata-rata rangkaian akan menjadi rata-rata daya sesaat pada satu siklus penuh dengan daya sesaat, p didefinisikan sebagai perkalian dari tegangan sesaat, v oleh arus sesaat, i.
Perhatikan bahwa karena fungsi sinusoidal periodik dan kontinu, daya rata-rata yang diberikan sepanjang waktu akan sama persis dengan daya rata-rata yang diberikan pada satu siklus tunggal.
Mari kita asumsikan bahwa bentuk gelombang dari tegangan dan arus keduanya sinusoidal, jadi kita ingat bahwa:

Karena daya sesaat adalah daya setiap saat, maka:
v = Vm sin(ωt+θv)
i = Im sin(ωt+θi)
p = [Vm sin(ωt+θv)] x [Im sin(ωt+θi)]
∴ p = Vm Im[sin(ωt+θv) sin(ωt+θi)]
Menerapkan identitas hasil-ke-jumlah trigonometri dari:

dan θ = θv - θi (perbedaan fasa antara tegangan dan bentuk gelombang saat ini) ke dalam persamaan di atas memberikan:

Di mana V dan I adalah nilai-nilai akar-rata-kuadrat (rms) dari bentuk gelombang sinusoidal, masing-masing v dan i , dan θ adalah perbedaan fasa antara dua bentuk gelombang. Karena itu kita dapat mengekspresikan kekuatan sesaat sebagai:
Persamaan ini menunjukkan kepada kita bahwa daya AC sesaat memiliki dua bagian yang berbeda dan oleh karena itu jumlah dari kedua istilah ini.
Istilah kedua adalah sinusoid dengan waktu yang bervariasi yang frekuensinya sama dengan dua kali frekuensi sudut supply karena 2ω bagian dari istilah tersebut. Namun istilah pertama adalah konstanta yang nilainya hanya bergantung pada perbedaan fasa, θ antara tegangan, (V) dan arus, (I).
Karena daya sesaat terus berubah dengan profil sinusoidal dari waktu ke waktu, ini membuatnya sulit untuk diukur. Oleh karena itu lebih nyaman, dan lebih mudah pada matematika untuk menggunakan nilai rata-rata atau mean dari daya. Jadi selama jumlah siklus yang tetap, nilai rata-rata daya sesaat dari sinusoidal diberikan hanya sebagai:
p = V x I cosθ
Di mana V dan I adalah nilai sinusoidal, dan θ (Theta) adalah sudut fasa antara tegangan dan arus. Unit daya dalam watt (W).
Daya AC yang dihamburkan dalam suatu rangkaian juga dapat ditemukan dari impedansi, (Z) rangkaian menggunakan tegangan, Vrms atau arus, Irms mengalir melalui rangkaian seperti yang ditunjukkan.
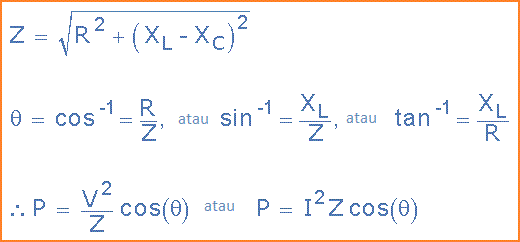
Dari atas, daya sesaat yang diserap oleh rangkaian diberikan sebagai:
p = v x i = 240 (sinωt+60°) x 5(sinωt+10°)
p = 240x5[ sin(314.2t+60°)sin(314.2t-10°)]
∴p = 1200[sin(314.2t+60°)sin(314.2t-10°)]
Menerapkan aturan rumus trigonometri dari atas memberikan:

Daya rata-rata kemudian dihitung sebagai:

Anda mungkin telah memperhatikan bahwa nilai daya rata-rata 205.2 watt juga merupakan nilai jangka pertama dari daya sesaat p(t) karena nilai konstanta istilah pertama ini adalah tingkat rata-rata atau rata-rata perubahan energi antara sumber dan beban.
Pertimbangkan rangkaian resistif murni (yaitu kapasitansi tak terbatas, C = ∞ dan nol induktansi, L = 0) dengan resistor yang terhubung ke catu daya AC, seperti yang ditunjukkan.

Ketika Resistor murni terhubung ke catu tegangan sinusoidal, arus yang mengalir melalui resistor akan bervariasi secara proporsional dengan tegangan supply, yaitu tegangan dan bentuk gelombang arus adalah “dalam-fasa” satu sama lain.
Karena perbedaan fasa antara bentuk gelombang tegangan dan bentuk gelombang arus adalah 0°, sudut fasa yang menghasilkan cos 0° akan sama dengan 1. Kemudian daya listrik yang dikonsumsi oleh resistor diberikan oleh:
cos(0°)=1
∴P = VxIx1 =VxI (watt, W)
Karena tegangan dan bentuk gelombang arus berada dalam fasa, yaitu kedua bentuk gelombang tersebut mencapai nilai puncaknya pada saat yang sama, dan juga melewati nol pada waktu yang sama, persamaan daya di atas berkurang menjadi hanya: V*I.
Oleh karena itu daya kapan saja dapat ditemukan dengan mengalikan kedua bentuk gelombang untuk menghasilkan volt-ampere. Ini disebut "Daya Nyata", ( P ) diukur dalam watt, (W), Kilowatt (kW), Megawatt (MW), dll.
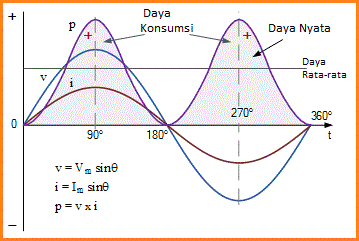
Diagram menunjukkan tegangan, arus dan bentuk gelombang daya yang sesuai. Karena bentuk gelombang tegangan dan arus keduanya dalam fasa, selama setengah siklus positif, ketika tegangan positif, arus juga positif sehingga daya positif, sebagai positif kali positif sama dengan positif.
Selama setengah siklus negatif, tegangan negatif, sehingga untuk arus menghasilkan daya menjadi positif, sebagai negatif kali negatif sama dengan positif.
Kemudian dalam rangkaian resistif murni, daya listrik dikonsumsi SEMUA waktu arus mengalir melalui resistor dan diberikan sebagai: P = V*I = I2R watt. Perhatikan bahwa baik V dan I dapat menjadi nilai rms mereka di mana: V = I*R dan I = V/R
Setiap kali tegangan berubah diterapkan pada kumparan induktif murni, "kembali" ggl dihasilkan oleh kumparan karena induktansi sendiri. Induktansi diri ini menentang dan membatasi setiap perubahan pada arus yang mengalir dalam coil.
Efek dari ggl-balik ini adalah bahwa arus tidak dapat meningkat segera melalui kumparan dalam-fasa dengan tegangan yang diberikan menyebabkan bentuk gelombang arus mencapai puncaknya atau nilai maksimum beberapa saat setelah itu dari tegangan.
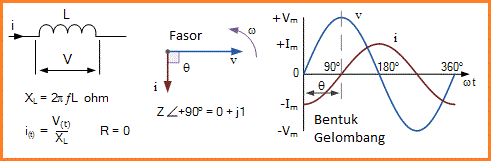
Hasilnya adalah bahwa dalam rangkaian induktif murni, arus selalu "tertinggal" (ELI) di belakang tegangan sebesar 90° (π/2) seperti yang ditunjukkan.
Bentuk gelombang di atas menunjukkan kepada kita tegangan sesaat dan arus sesaat melintasi kumparan induktif murni sebagai fungsi waktu. Arus maksimum, I max terjadi pada seperempat penuh dari siklus (90°) setelah maksimum (puncak) nilai tegangan.
Disini arus ditunjukkan dengan nilai maksimum negatif pada awal siklus tegangan dan melewati nol meningkatkan nilai maksimum positif ketika gelombang tegangan adalah pada nilai maksimum pada 90°.
Jadi karena tegangan dan bentuk gelombang arus tidak lagi naik dan turun bersama-sama, tetapi alih-alih pergeseran fasa 90° (π/2) diperkenalkan dalam coil, maka tegangan dan bentuk gelombang arus adalah "diluar-fasa" dengan masing-masing lain sebagai tegangan memimpin arus sebesar 90°.
Karena perbedaan fasa antara bentuk gelombang tegangan dan bentuk gelombang arus adalah 90°, maka sudut fasa menghasilkan cos 90° = 0.
Oleh karena itu daya listrik yang disimpan oleh induktor murni, QL diberikan oleh:
cos(90°) = 0
∴P = V x I x 0 = 0 (watt)
Maka jelas, induktor murni tidak mengkonsumsi atau menghilangkan daya nyata atau real, tetapi karena kami memiliki tegangan dan arus penggunaan cos (θ) dalam ekspresi: P = V*I*cos(θ) untuk induktor murni tidak lagi valid.
Hasil dari arus dan tegangan dalam hal ini adalah daya imajiner, yang biasa disebut "Daya Reaktif", ( Q ) diukur dalam volt-ampere reaktif, (VAr), Kilo-voltamperes reaktif (KVAr), dll.
Voltamperes reaktif, VAr tidak harus campur dengan watt, (W) yang digunakan untuk daya nyata. VAr mewakili hasil dari volt dan ampere yang 90° diluar-fasa satu sama lain. Untuk mengidentifikasi daya rata-rata reaktif secara matematis, fungsi sinus digunakan. Maka persamaan untuk daya reaktif rata-rata dalam induktor menjadi:
sin (+90°) = +1
∴QL =V x I x + 1 = V x I (Var)
Seperti daya nyata (P), daya reaktif, (Q) juga tergantung pada tegangan dan arus, tetapi juga sudut fasa di antara mereka. Oleh karena itu hasil dari tegangan dan bagian komponen dari arus yang 90° out-of-fasa dengan tegangan seperti yang ditunjukkan.

Pada setengah positif dari bentuk gelombang tegangan antara sudut 0° dan 90°, arus induktor negatif sedangkan tegangan supply positif. Oleh karena itu, volt dan hasil ampere memberikan daya negatif sebagai negatif kali positif sama dengan negatif.
Antara 90° dan 180°, baik arus dan tegangan bentuk gelombang positif nilai menghasilkan daya positif. Daya positif ini menunjukkan bahwa coil mengkonsumsi energi listrik dari supply.
Pada setengah negatif dari bentuk gelombang tegangan antara 180° dan 270°, terdapat tegangan negatif dan arus positif yang menunjukkan daya negatif.
Daya negatif ini menunjukkan bahwa coil mengembalikan energi listrik yang tersimpan ke supply. Antara 270° dan 360°, baik induktor arus dan tegangan suplai keduanya negatif yang dihasilkan dalam periode daya positif.
Kemudian selama satu siklus penuh dari bentuk gelombang tegangan, kita memiliki dua pulsa daya positif dan negatif yang identik dengan nilai rata-rata nol sehingga tidak ada daya nyata yang digunakan karena daya bergantian mengalir ke dan dari sumber.
Ini berarti bahwa daya total yang diambil oleh induktor murni selama satu siklus penuh adalah nol, sehingga daya reaktif induktor tidak melakukan pekerjaan nyata.

Bentuk gelombang menunjukkan kepada kita tegangan dan arus melintasi kapasitor murni sebagai fungsi waktu. Arus maksimum, Im terjadi seperempat penuh siklus (90°) sebelum nilai maksimum (puncak) tegangan.
Disini arus ditunjukkan dengan nilai maksimum positif pada awal siklus tegangan dan melewati nol, penurunan nilai maksimum negatif ketika gelombang tegangan adalah pada nilai maksimum pada 90°. Fasa sebaliknya bergeser ke rangkaian induktif murni.

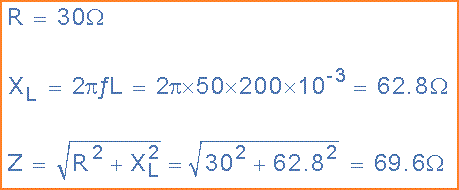


Dalam rangkaian DC, daya yang dikonsumsi hanyalah hasil dari tegangan DC kali arus DC, diberikan dalam watt. Namun, untuk rangkaian AC dengan komponen reaktif kita harus menghitung daya yang dikonsumsi secara berbeda.
Daya listrik adalah "kecepatan" di mana energi dikonsumsi dalam suatu rangkaian dan dengan demikian semua komponen dan perangkat listrik dan elektronik memiliki batas jumlah daya listrik yang dapat mereka tangani dengan aman. Misalnya, resistor 1/4 watt atau amplifier 20 watt.
Daya listrik dapat beragam waktu baik sebagai kuantitas DC atau sebagai kuantitas AC. Jumlah daya dalam suatu rangkaian pada saat kapan saja disebut daya sesaat dan diberikan oleh hubungan daya yang terkenal (P = V*I). Jadi satu watt (yang merupakan tingkat pengeluaran energi pada satu joule per detik) akan sama dengan hasil volt-ampere satu volt kali satu ampere.
Kemudian daya yang diserap atau disuplai oleh elemen rangkaian adalah hasil dari tegangan, V melintasi elemen, dan arus, I mengalir melaluinya. Jadi jika kita memiliki rangkaian DC dengan resistansi "R" ohm, daya yang dihamburkan oleh resistor dalam watt diberikan oleh salah satu rumus umum berikut:
Power/Daya Listrik

Di mana: V adalah tegangan DC, I adalah arus dc dan R adalah nilai resistansi.
Jadi daya dalam rangkaian listrik hanya ada ketika tegangan dan arus ada, yang tidak ada kondisi rangkaian terbuka atau rangkaian tertutup. Pertimbangkan contoh sederhana berikut dari rangkaian DC resistif standar:
Rangkaian Resistif DC

Power/Daya Listrik di Rangkaian AC
Dalam rangkaian DC, tegangan dan arus pada umumnya konstan, yang tidak bervariasi dengan waktu karena tidak ada bentuk gelombang sinusoidal yang terkait dengan supply. Namun dalam rangkaian AC, nilai sesaat dari tegangan, arus dan karena itu daya terus berubah dipengaruhi oleh supply.Jadi kita tidak dapat menghitung daya di rangkaian AC dengan cara yang sama seperti di rangkaian DC, tetapi kita masih bisa mengatakan bahwa daya (p) sama dengan tegangan (v) dikalikan dengan arus (i).
Poin penting lainnya adalah bahwa rangkaian AC mengandung reaktansi, sehingga ada komponen daya sebagai hasil dari medan magnet dan/atau listrik yang dibuat oleh komponen.
Hasilnya adalah bahwa tidak seperti komponen resistif murni, daya ini disimpan dan kemudian dikembalikan ke supply ketika gelombang sinusoidal melewati satu siklus periodik lengkap. Dengan demikian, daya rata-rata yang diserap oleh suatu rangkaian adalah jumlah daya yang disimpan dan daya yang dikembalikan selama satu siklus lengkap.
Jadi konsumsi daya rata-rata rangkaian akan menjadi rata-rata daya sesaat pada satu siklus penuh dengan daya sesaat, p didefinisikan sebagai perkalian dari tegangan sesaat, v oleh arus sesaat, i.
Perhatikan bahwa karena fungsi sinusoidal periodik dan kontinu, daya rata-rata yang diberikan sepanjang waktu akan sama persis dengan daya rata-rata yang diberikan pada satu siklus tunggal.
Mari kita asumsikan bahwa bentuk gelombang dari tegangan dan arus keduanya sinusoidal, jadi kita ingat bahwa:
Bentuk Gelombang Tegangan Sinusoidal

Karena daya sesaat adalah daya setiap saat, maka:
p = v x i
dimana:v = Vm sin(ωt+θv)
i = Im sin(ωt+θi)
p = [Vm sin(ωt+θv)] x [Im sin(ωt+θi)]
∴ p = Vm Im[sin(ωt+θv) sin(ωt+θi)]
Menerapkan identitas hasil-ke-jumlah trigonometri dari:

dan θ = θv - θi (perbedaan fasa antara tegangan dan bentuk gelombang saat ini) ke dalam persamaan di atas memberikan:

Di mana V dan I adalah nilai-nilai akar-rata-kuadrat (rms) dari bentuk gelombang sinusoidal, masing-masing v dan i , dan θ adalah perbedaan fasa antara dua bentuk gelombang. Karena itu kita dapat mengekspresikan kekuatan sesaat sebagai:
Persamaan Daya AC Sesaat
p = VIcosθ - VIcos(2ωt+θ)Persamaan ini menunjukkan kepada kita bahwa daya AC sesaat memiliki dua bagian yang berbeda dan oleh karena itu jumlah dari kedua istilah ini.
Istilah kedua adalah sinusoid dengan waktu yang bervariasi yang frekuensinya sama dengan dua kali frekuensi sudut supply karena 2ω bagian dari istilah tersebut. Namun istilah pertama adalah konstanta yang nilainya hanya bergantung pada perbedaan fasa, θ antara tegangan, (V) dan arus, (I).
Karena daya sesaat terus berubah dengan profil sinusoidal dari waktu ke waktu, ini membuatnya sulit untuk diukur. Oleh karena itu lebih nyaman, dan lebih mudah pada matematika untuk menggunakan nilai rata-rata atau mean dari daya. Jadi selama jumlah siklus yang tetap, nilai rata-rata daya sesaat dari sinusoidal diberikan hanya sebagai:
p = V x I cosθ
Di mana V dan I adalah nilai sinusoidal, dan θ (Theta) adalah sudut fasa antara tegangan dan arus. Unit daya dalam watt (W).
Daya AC yang dihamburkan dalam suatu rangkaian juga dapat ditemukan dari impedansi, (Z) rangkaian menggunakan tegangan, Vrms atau arus, Irms mengalir melalui rangkaian seperti yang ditunjukkan.
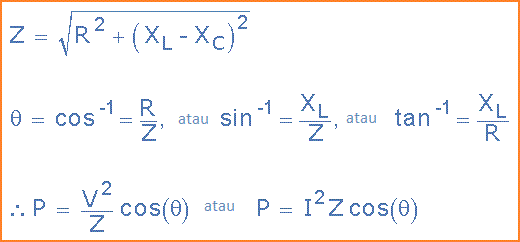
Contoh Daya AC No.1
Nilai tegangan dan arus supply sinusoidal 50Hz diberikan sebagai: vt = 240 sin (ωt +60°) Volt dan it = 5 sin (ωt-10° ) Amps masing-masing. Temukan nilai daya sesaat dan daya rata-rata yang diserap oleh rangkaian.Dari atas, daya sesaat yang diserap oleh rangkaian diberikan sebagai:
p = v x i = 240 (sinωt+60°) x 5(sinωt+10°)
p = 240x5[ sin(314.2t+60°)sin(314.2t-10°)]
∴p = 1200[sin(314.2t+60°)sin(314.2t-10°)]
Menerapkan aturan rumus trigonometri dari atas memberikan:

Daya rata-rata kemudian dihitung sebagai:

Anda mungkin telah memperhatikan bahwa nilai daya rata-rata 205.2 watt juga merupakan nilai jangka pertama dari daya sesaat p(t) karena nilai konstanta istilah pertama ini adalah tingkat rata-rata atau rata-rata perubahan energi antara sumber dan beban.
Daya AC di Rangkaian Resistif Murni
Kita telah melihat sejauh ini, bahwa dalam rangkaian DC, daya sama dengan hasil tegangan dan arus dan hubungan ini juga berlaku untuk rangkaian AC murni resistif. Resistor adalah perangkat listrik yang mengkonsumsi energi dan daya dalam sebuah resistor diberikan oleh p = VI = I2R = V2/R. Daya ini selalu positif.Pertimbangkan rangkaian resistif murni (yaitu kapasitansi tak terbatas, C = ∞ dan nol induktansi, L = 0) dengan resistor yang terhubung ke catu daya AC, seperti yang ditunjukkan.
Rangkaian Resistif Murni

Ketika Resistor murni terhubung ke catu tegangan sinusoidal, arus yang mengalir melalui resistor akan bervariasi secara proporsional dengan tegangan supply, yaitu tegangan dan bentuk gelombang arus adalah “dalam-fasa” satu sama lain.
Karena perbedaan fasa antara bentuk gelombang tegangan dan bentuk gelombang arus adalah 0°, sudut fasa yang menghasilkan cos 0° akan sama dengan 1. Kemudian daya listrik yang dikonsumsi oleh resistor diberikan oleh:
Daya Listrik pada Resistor Murni
P = VxIcosθcos(0°)=1
∴P = VxIx1 =VxI (watt, W)
Karena tegangan dan bentuk gelombang arus berada dalam fasa, yaitu kedua bentuk gelombang tersebut mencapai nilai puncaknya pada saat yang sama, dan juga melewati nol pada waktu yang sama, persamaan daya di atas berkurang menjadi hanya: V*I.
Oleh karena itu daya kapan saja dapat ditemukan dengan mengalikan kedua bentuk gelombang untuk menghasilkan volt-ampere. Ini disebut "Daya Nyata", ( P ) diukur dalam watt, (W), Kilowatt (kW), Megawatt (MW), dll.
Gelombang AC untuk Resistor Murni

Diagram menunjukkan tegangan, arus dan bentuk gelombang daya yang sesuai. Karena bentuk gelombang tegangan dan arus keduanya dalam fasa, selama setengah siklus positif, ketika tegangan positif, arus juga positif sehingga daya positif, sebagai positif kali positif sama dengan positif.
Selama setengah siklus negatif, tegangan negatif, sehingga untuk arus menghasilkan daya menjadi positif, sebagai negatif kali negatif sama dengan positif.
Kemudian dalam rangkaian resistif murni, daya listrik dikonsumsi SEMUA waktu arus mengalir melalui resistor dan diberikan sebagai: P = V*I = I2R watt. Perhatikan bahwa baik V dan I dapat menjadi nilai rms mereka di mana: V = I*R dan I = V/R
Daya AC di Rangkaian Induktif Murni
Dalam rangkaian induktif murni (yaitu kapasitansi tak terbatas, C = ∞ dan nol resistansi, R = 0) L Henries, tegangan dan bentuk gelombang arus tidak dalam-fasa.Setiap kali tegangan berubah diterapkan pada kumparan induktif murni, "kembali" ggl dihasilkan oleh kumparan karena induktansi sendiri. Induktansi diri ini menentang dan membatasi setiap perubahan pada arus yang mengalir dalam coil.
Efek dari ggl-balik ini adalah bahwa arus tidak dapat meningkat segera melalui kumparan dalam-fasa dengan tegangan yang diberikan menyebabkan bentuk gelombang arus mencapai puncaknya atau nilai maksimum beberapa saat setelah itu dari tegangan.
Hasilnya adalah bahwa dalam rangkaian induktif murni, arus selalu "tertinggal" (ELI) di belakang tegangan sebesar 90° (π/2) seperti yang ditunjukkan.
Rangkaian Induktif Murni

Bentuk gelombang di atas menunjukkan kepada kita tegangan sesaat dan arus sesaat melintasi kumparan induktif murni sebagai fungsi waktu. Arus maksimum, I max terjadi pada seperempat penuh dari siklus (90°) setelah maksimum (puncak) nilai tegangan.
Disini arus ditunjukkan dengan nilai maksimum negatif pada awal siklus tegangan dan melewati nol meningkatkan nilai maksimum positif ketika gelombang tegangan adalah pada nilai maksimum pada 90°.
Jadi karena tegangan dan bentuk gelombang arus tidak lagi naik dan turun bersama-sama, tetapi alih-alih pergeseran fasa 90° (π/2) diperkenalkan dalam coil, maka tegangan dan bentuk gelombang arus adalah "diluar-fasa" dengan masing-masing lain sebagai tegangan memimpin arus sebesar 90°.
Karena perbedaan fasa antara bentuk gelombang tegangan dan bentuk gelombang arus adalah 90°, maka sudut fasa menghasilkan cos 90° = 0.
Oleh karena itu daya listrik yang disimpan oleh induktor murni, QL diberikan oleh:
Daya Nyata dalam Induktor Murni
P = V x I cosθcos(90°) = 0
∴P = V x I x 0 = 0 (watt)
Maka jelas, induktor murni tidak mengkonsumsi atau menghilangkan daya nyata atau real, tetapi karena kami memiliki tegangan dan arus penggunaan cos (θ) dalam ekspresi: P = V*I*cos(θ) untuk induktor murni tidak lagi valid.
Hasil dari arus dan tegangan dalam hal ini adalah daya imajiner, yang biasa disebut "Daya Reaktif", ( Q ) diukur dalam volt-ampere reaktif, (VAr), Kilo-voltamperes reaktif (KVAr), dll.
Voltamperes reaktif, VAr tidak harus campur dengan watt, (W) yang digunakan untuk daya nyata. VAr mewakili hasil dari volt dan ampere yang 90° diluar-fasa satu sama lain. Untuk mengidentifikasi daya rata-rata reaktif secara matematis, fungsi sinus digunakan. Maka persamaan untuk daya reaktif rata-rata dalam induktor menjadi:
Daya Reaktif dalam Induktor Murni
QL = V x I sinθsin (+90°) = +1
∴QL =V x I x + 1 = V x I (Var)
Seperti daya nyata (P), daya reaktif, (Q) juga tergantung pada tegangan dan arus, tetapi juga sudut fasa di antara mereka. Oleh karena itu hasil dari tegangan dan bagian komponen dari arus yang 90° out-of-fasa dengan tegangan seperti yang ditunjukkan.
Gelombang Daya AC untuk Induktor Murni

Pada setengah positif dari bentuk gelombang tegangan antara sudut 0° dan 90°, arus induktor negatif sedangkan tegangan supply positif. Oleh karena itu, volt dan hasil ampere memberikan daya negatif sebagai negatif kali positif sama dengan negatif.
Antara 90° dan 180°, baik arus dan tegangan bentuk gelombang positif nilai menghasilkan daya positif. Daya positif ini menunjukkan bahwa coil mengkonsumsi energi listrik dari supply.
Pada setengah negatif dari bentuk gelombang tegangan antara 180° dan 270°, terdapat tegangan negatif dan arus positif yang menunjukkan daya negatif.
Daya negatif ini menunjukkan bahwa coil mengembalikan energi listrik yang tersimpan ke supply. Antara 270° dan 360°, baik induktor arus dan tegangan suplai keduanya negatif yang dihasilkan dalam periode daya positif.
Kemudian selama satu siklus penuh dari bentuk gelombang tegangan, kita memiliki dua pulsa daya positif dan negatif yang identik dengan nilai rata-rata nol sehingga tidak ada daya nyata yang digunakan karena daya bergantian mengalir ke dan dari sumber.
Ini berarti bahwa daya total yang diambil oleh induktor murni selama satu siklus penuh adalah nol, sehingga daya reaktif induktor tidak melakukan pekerjaan nyata.
Daya AC di Rangkaian Kapasitif Murni
Sebuah rangkaian kapasitif murni (yaitu nol induktansi, L = 0 dan resistansi tak terbatas, R = ∞) dari C Farads, memiliki sifat menunda perubahan tegangan yang melintasinya. Kapasitor menyimpan energi listrik dalam bentuk medan listrik dalam dielektrik sehingga kapasitor murni tidak menghilangkan energi apa pun, tetapi menyimpannya.
Dalam rangkaian kapasitif murni, tegangan tidak dapat meningkat dalam fasa dengan arus karena perlu "mengisi ulang" plat kapasitor terlebih dahulu. Hal ini menyebabkan bentuk gelombang tegangan mencapai puncaknya atau nilai maksimum beberapa saat setelah itu dari arus.
Hasilnya adalah bahwa dalam rangkaian kapasitif murni, arus selalu "mengarah" (ICE) tegangan sebesar 90° (ω/2) seperti yang ditunjukkan.
Hasilnya adalah bahwa dalam rangkaian kapasitif murni, arus selalu "mengarah" (ICE) tegangan sebesar 90° (ω/2) seperti yang ditunjukkan.
Rangkaian Kapasitif Murni

Bentuk gelombang menunjukkan kepada kita tegangan dan arus melintasi kapasitor murni sebagai fungsi waktu. Arus maksimum, Im terjadi seperempat penuh siklus (90°) sebelum nilai maksimum (puncak) tegangan.
Disini arus ditunjukkan dengan nilai maksimum positif pada awal siklus tegangan dan melewati nol, penurunan nilai maksimum negatif ketika gelombang tegangan adalah pada nilai maksimum pada 90°. Fasa sebaliknya bergeser ke rangkaian induktif murni.
Jadi untuk rangkaian kapasitif murni, sudut fasa θ = -90° dan persamaan untuk daya reaktif rata-rata dalam kapasitor menjadi:
Daya Reaktif dalam Kapasitor Murni
QC = V x I sinθ
sin (-90°) = -1
∴QC =V x I x -1 = V x I (Var)
sin (-90°) = -1
∴QC =V x I x -1 = V x I (Var)
Di mana –V*I*sin (θ) adalah gelombang sinus negatif. Juga simbol untuk daya reaktif kapasitif QC dengan unit yang sama ukuran, yang volt-ampere reaktif (VAR) seperti yang dari induktor.
Kemudian kita dapat melihat bahwa sama seperti rangkaian induktif murni di atas, kapasitor murni tidak mengkonsumsi atau menghilangkan daya nyata atau real, P.
Kemudian kita dapat melihat bahwa sama seperti rangkaian induktif murni di atas, kapasitor murni tidak mengkonsumsi atau menghilangkan daya nyata atau real, P.
Gelombang Daya AC untuk Kapasitor Murni

Pada setengah positif dari bentuk gelombang tegangan antara sudut 0° dan 90°, baik bentuk gelombang arus maupun tegangan bernilai positif sehingga menghasilkan daya positif yang dikonsumsi.
Antara 90° dan 180°, kapasitor arus adalah negatif dan tegangan supply masih positif. Oleh karena itu, hasil volt-ampere memberikan daya negatif sebagai negatif kali positif sama dengan negatif. Daya negatif ini menunjukkan bahwa coil mengembalikan energi listrik yang tersimpan ke supply.
Antara 90° dan 180°, kapasitor arus adalah negatif dan tegangan supply masih positif. Oleh karena itu, hasil volt-ampere memberikan daya negatif sebagai negatif kali positif sama dengan negatif. Daya negatif ini menunjukkan bahwa coil mengembalikan energi listrik yang tersimpan ke supply.
Pada setengah negatif dari bentuk gelombang tegangan antara 180° dan 270°, baik arus kapasitor dan tegangan supply bernilai negatif sehingga menghasilkan periode daya positif.
Periode daya positif ini menunjukkan bahwa coil mengkonsumsi energi listrik dari supply. Antara 270° dan 360°, ada tegangan negatif dan arus positif menunjukkan sekali lagi daya negatif.
Periode daya positif ini menunjukkan bahwa coil mengkonsumsi energi listrik dari supply. Antara 270° dan 360°, ada tegangan negatif dan arus positif menunjukkan sekali lagi daya negatif.
Kemudian selama satu siklus penuh dari gelombang tegangan situasi yang sama ada untuk rangkaian induktif murni di mana kita memiliki dua pulsa daya positif dan negatif yang identik dengan nilai rata-rata nol.
Dengan demikian daya yang dikirim dari sumber ke kapasitor persis sama dengan daya yang dikembalikan ke sumber oleh kapasitor sehingga tidak ada daya nyata yang digunakan karena daya bergantian mengalir ke dan dari sumber.
Ini berarti bahwa daya total yang diambil oleh kapasitor murni selama satu siklus penuh adalah nol, sehingga daya reaktif kapasitor tidak melakukan pekerjaan nyata.
Dengan demikian daya yang dikirim dari sumber ke kapasitor persis sama dengan daya yang dikembalikan ke sumber oleh kapasitor sehingga tidak ada daya nyata yang digunakan karena daya bergantian mengalir ke dan dari sumber.
Ini berarti bahwa daya total yang diambil oleh kapasitor murni selama satu siklus penuh adalah nol, sehingga daya reaktif kapasitor tidak melakukan pekerjaan nyata.
Contoh Daya Listrik No.2

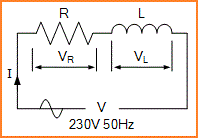
Coil solenoid dengan resistansi 30 ohm dan induktansi 200mH terhubung ke 230VAC, supply 50Hz. Hitung: (a) impedansi solenoid, (b) arus yang dikonsumsi oleh solenoid, (c) sudut fasa antara arus dan tegangan yang diberikan, dan (d) daya rata-rata yang dikonsumsi solenoid.
Data yang diberikan: R = 30Ω, L = 200mH, V = 230V dan ƒ = 50Hz.
(a) Impedansi (Z) dari coil solenoid:
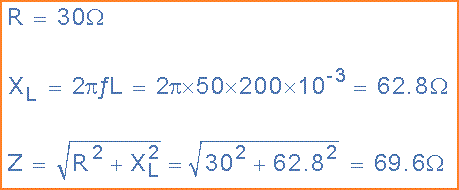
(b) Arus (I) dikonsumsi oleh coil solenoid:

(c) Sudut fasa, θ:

(d) Daya AC rata-rata yang dikonsumsi oleh coil solenoid:
P = V x I sinθ
P = 230 x 3.3 x cos(64.5°)
∴ P = 327 watt
∴ P = 327 watt
Ringkasan Daya Listrik AC
Kita telah melihat di sini bahwa di rangkaian AC, tegangan dan arus yang mengalir dalam rangkaian pasif murni biasanya diluar-fasa dan, akibatnya, mereka tidak dapat digunakan untuk menyelesaikan pekerjaan nyata apa pun.
Kita juga telah melihat bahwa dalam rangkaian arus searah (DC), daya listrik sama dengan tegangan kali arus, atau P = V*I, tetapi kita tidak dapat menghitungnya dengan cara yang sama seperti untuk rangkaian AC seperti yang kita butuhkan. memperhitungkan perbedaan fasa.
Kita juga telah melihat bahwa dalam rangkaian arus searah (DC), daya listrik sama dengan tegangan kali arus, atau P = V*I, tetapi kita tidak dapat menghitungnya dengan cara yang sama seperti untuk rangkaian AC seperti yang kita butuhkan. memperhitungkan perbedaan fasa.
Dalam rangkaian resistif murni, arus dan tegangan keduanya dalam-fasa dan semua daya listrik dikonsumsi oleh resistansi, biasanya sebagai panas. Akibatnya, tidak ada daya listrik yang dikembalikan kembali ke sumber supply atau rangkaian.
Namun, dalam rangkaian murni induktif atau kapasitif murni yang mengandung reaktansi, (X) arus akan mengarahkan atau memperlambat tegangan dengan tepat 90° (sudut fasa) sehingga daya disimpan dan dikembalikan ke sumbernya. Dengan demikian daya rata-rata yang dihitung selama satu siklus periodik penuh akan sama dengan nol.
Daya listrik yang dikonsumsi oleh suatu resistansi, (R) disebut daya real atau nyata dan hanya diperoleh dengan mengalikan tegangan rms dengan arus rms. Daya yang disimpan oleh reaktansi, (X) disebut daya reaktif dan diperoleh dengan mengalikan tegangan, arus, dan sinus sudut fasa di antara mereka.
Simbol untuk sudut fasa adalah θ (Theta) dan yang mewakili inefisiensi dari rangkaian AC sehubungan dengan total impedansi reaktif (Z) yang menentang aliran arus dalam rangkaian.