Beda Fasa dan Pergeseran Fasa
Beda Fasa digunakan untuk menggambarkan beda dalam derajat atau radian ketika dua atau lebih kuantitas bolak-balik mencapai nilai maksimum atau nolnya Sebelumnya kita melihat bahwa Gelombang Sinusoidal adalah kuantitas bolak-balik yang dapat disajikan secara grafis dalam domain waktu sepanjang sumbu nol horisontal.
Kita juga melihat bahwa sebagai kuantitas bolak-balik, gelombang sinusoisal memiliki nilai maksimum positif pada waktu π/2, nilai maksimum negatif pada waktu 3π/2, dengan nilai nol terjadi di sepanjang garis dasar pada 0, π dan 2π. Namun, tidak semua bentuk gelombang sinusoidal akan melewati persis melalui titik nol sumbu pada saat yang sama, tetapi mungkin “bergeser” ke kanan atau ke kiri dari 0° oleh beberapa nilai bila dibandingkan dengan gelombang sinusoidal lain.
Misalnya, membandingkan bentuk gelombang tegangan dengan bentuk gelombang arus. Ini kemudian menghasilkan pergeseran sudut atau beda fasa antara dua bentuk gelombang sinusoidal. Setiap gelombang sinus yang tidak melewati nol pada t = 0 memiliki pergeseran fasa.
Beda fasa atau pergeseran fasa sebagaimana juga disebut sebagai Bentuk Gelombang Sinusoidal adalah sudut Φ (huruf Yunani Phi), dalam derajat atau radian yang bentuk gelombangnya telah bergeser dari titik referensi tertentu sepanjang sumbu nol horisontal. Dengan kata lain pergeseran fasa adalah Beda lateral antara dua atau lebih bentuk gelombang sepanjang sumbu umum dan bentuk gelombang sinusoidal dari frekuensi yang sama dapat memiliki beda fasa.
Beda fasa, Φ dari gelombang bolak-balik dapat bervariasi dari antara 0 hingga periode waktu maksimumnya, T dari gelombang selama satu siklus lengkap dan ini dapat di mana saja di sepanjang sumbu horizontal antara, Φ = 0 hingga 2π (radian) atau Φ = 0 hingga 360° tergantung pada unit sudut yang digunakan.
Beda fasa juga dapat dinyatakan sebagai pergeseran waktu dari τ di detik mewakili sebagian kecil dari periode waktu, T misalnya, + 10mS atau - 50US tetapi umumnya itu lebih umum untuk menyatakan Beda fasa sebagai pengukuran sudut. Maka persamaan untuk nilai sesaat dari tegangan sinusoidal atau bentuk gelombang arus yang kami kembangkan dalam bentuk gelombang Sinusoidal sebelumnya perlu dimodifikasi untuk memperhitungkan sudut fasa bentuk gelombang dan ekspresi umum baru ini menjadi.
Dimana:
Am -adalah amplitudo gelombang.
ωt - adalah frekuensi sudut dari bentuk gelombang dalam radian / detik.
Φ(phi) - adalah sudut fasa dalam derajat atau radian bahwa gelombang telah bergeser ke kiri atau kanan dari titik referensi.
Jika kemiringan positif dari bentuk gelombang sinusoidal melewati sumbu horizontal "sebelum" t = 0 maka bentuk gelombang telah bergeser ke kiri sehingga Φ>0, dan sudut fasa akan bersifat positif, +Φ memberikan sudut fasa terkemuka. Dengan kata lain itu muncul lebih awal daripada 0° menghasilkan rotasi berlawanan arah jarum jam dari vektor.
Demikian juga, jika kemiringan positif dari gelombang sinusoidal melewati horisontal sumbu x beberapa waktu “setelah” t = 0 maka gelombang telah bergeser ke kanan sehingga Φ<0, dan sudut fasa akan bersifat negatif -Φ menghasilkan sudut fasa lagging (tertinggal) seperti yang muncul kemudian dalam waktu dari 0° menghasilkan rotasi searah jarum jam vektor. Kedua kasus ditunjukkan di bawah ini.

Pertama, mari kita perhatikan bahwa dua kuantitas bolak-balik seperti tegangan, v dan arus, i memiliki frekuensi yang sama f di Hertz. Karena frekuensi dua kuantitas adalah sama dengan kecepatan sudut, ω juga harus sama. Jadi kapan saja kita dapat mengatakan bahwa fasa tegangan, v akan sama dengan fasa arus, i. Maka sudut rotasi dalam periode waktu tertentu akan selalu sama dan beda fasa antara dua jumlah v dan i karena itu akan menjadi nol dan Φ = 0.
Sebagai frekuensi tegangan, v dan arus, i adalah sama mereka harus mencapai nilai positif, negatif dan nol maksimum selama satu siklus penuh pada waktu yang sama (walaupun amplitudo mereka mungkin berbeda). Kemudian dua kuantitas bolak-balik, v dan i dikatakan "dalam-fasa".

Sekarang mari kita perhatikan bahwa tegangan, v dan arus, i memiliki beda fasa antara mereka sendiri 30°, jadi (Φ = 30° atau π/6 radian). Karena kedua kuantitas bolak-balik berputar pada kecepatan yang sama, yaitu mereka memiliki frekuensi yang sama, beda fasa ini akan tetap konstan untuk semua instance dalam waktu, maka beda fasa 30° antara dua kuantitas diwakili oleh phi, Φ seperti yang ditunjukkan di bawah ini.

Bentuk gelombang tegangan di atas dimulai dari nol di sepanjang sumbu referensi horisontal, tetapi pada saat yang bersamaan, bentuk gelombang arus masih bernilai negatif dan tidak melewati sumbu referensi ini sampai 30° selanjutnya. Kemudian pada Beda Fasa antara kedua bentuk gelombang saat arus melintasi sumbu referensi horisontal mencapai puncak maksimum dan nilai nol setelah bentuk gelombang tegangan.
Karena dua bentuk gelombang tidak lagi "dalam-fasa", oleh karena itu mereka harus "keluar-fasa" dengan jumlah yang ditentukan oleh phi, Φ dan dalam contoh kita ini adalah 30°. Jadi kita dapat mengatakan bahwa dua bentuk gelombang sekarang 30° di luar fasa.
Bentuk gelombang arus juga bisa dikatakan "tertinggal" di belakang bentuk gelombang tegangan oleh sudut fasa, Φ. Kemudian dalam contoh kami di atas dua bentuk gelombang memiliki Beda Fasa Tertinggal sehingga ekspresi untuk tegangan dan arus di atas akan diberikan sebagai.
Tegangan (vt) = Vm sinωt
Arus (it) = Im sin (ωt-θ)
di mana, i Tertinggal v dengan sudut Φ
Demikian juga, jika arus, i memiliki nilai positif dan melintasi sumbu referensi mencapai puncak maksimum dan nilai nol pada beberapa waktu sebelum tegangan, v maka bentuk gelombang arus akan "memimpin" tegangan dengan beberapa sudut fasa. Kemudian kedua bentuk gelombang tersebut dikatakan memiliki Beda Fasa Terkemuka dan ekspresi untuk tegangan dan arus akan.
Tegangan (vt) = Vm sinωt
Arus (it) = Im sin (ωt+θ)
di mana, i Memimpin v dengan sudut Φ
Sudut fasa gelombang sinus dapat digunakan untuk menggambarkan hubungan satu gelombang sinus dengan yang lain dengan menggunakan istilah "Leading/memimpin" dan "Lagging/tertinggal" untuk menunjukkan hubungan antara dua bentuk gelombang sinusoidal dari frekuensi yang sama, diplot ke sumbu referensi yang sama.
Dalam contoh di atas dua bentuk gelombang yang diluar fasa dengan 30°. Jadi kita dapat dengan benar mengatakan bahwa i tertinggal v atau kita dapat mengatakan bahwa v memimpin i sampai 30° tergantung pada yang kita pilih sebagai referensi kita.
Hubungan antara kedua bentuk gelombang dan sudut fasa yang dihasilkan dapat diukur di mana saja di sepanjang sumbu nol horizontal yang dilalui setiap gelombang dengan arah "kemiringan yang sama" baik positif atau negatif.
Dalam rangkaian daya AC kemampuan ini untuk menggambarkan hubungan antara tegangan dan gelombang sinus arus dalam rangkaian yang sama sangat penting dan membentuk dasar analisis rangkaian AC.
Gelombang Cosinus, biasanya hanya disebut “cos”, adalah sama pentingnya dengan gelombang sinus di bidang teknik listrik. Gelombang cosinus memiliki bentuk yang sama dengan gelombang sinus yang merupakan fungsi sinusoidal, tetapi digeser oleh +90° atau seperempat penuh periode di depannya.
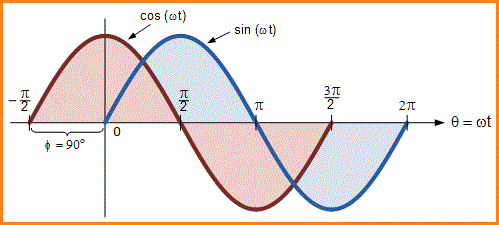
Atau, kita juga dapat mengatakan bahwa gelombang sinus adalah gelombang cosinus yang telah bergeser ke arah lain oleh -90°. Bagaimanapun juga ketika berhadapan dengan gelombang sinus atau gelombang cosinus dengan sudut aturan berikut akan selalu berlaku.
sin (ωt + ф) = cos(ωt + ф - 90°)
Ketika membandingkan dua bentuk gelombang sinusoidal, lebih umum untuk mengekspresikan hubungan mereka sebagai sinus atau cosinus dengan amplitudo positif dan ini dicapai dengan menggunakan rumus matematika berikut.
-sin (ωt) = sin(ωt ± 180°)
-cos (ωt) = cos(ωt ± 180°)
-cos (ωt) = sin(ωt ± 270°)
±sin (ωt) = cos(ωt ± 90°)
±cos (ωt) = sin(ωt ± 90°)
-sin (ωt) = sin(-ωt)
cos (ωt) = cos(-ωt)
Dengan menggunakan hubungan-hubungan di atas, kita dapat mengubah bentuk gelombang sinusoidal dengan atau tanpa beda sudut atau fasa dari salah satu gelombang sinus menjadi gelombang cosinus atau sebaliknya.
Dalam tutorial berikutnya tentang Fasor kita akan menggunakan metode grafis untuk mewakili atau membandingkan beda fasa antara dua sinusoidal dengan melihat representasi fasor kuantitas AC fasa tunggal bersama dengan beberapa aljabar fasor yang berkaitan dengan penambahan matematis dua atau lebih fasor.
Kita juga melihat bahwa sebagai kuantitas bolak-balik, gelombang sinusoisal memiliki nilai maksimum positif pada waktu π/2, nilai maksimum negatif pada waktu 3π/2, dengan nilai nol terjadi di sepanjang garis dasar pada 0, π dan 2π. Namun, tidak semua bentuk gelombang sinusoidal akan melewati persis melalui titik nol sumbu pada saat yang sama, tetapi mungkin “bergeser” ke kanan atau ke kiri dari 0° oleh beberapa nilai bila dibandingkan dengan gelombang sinusoidal lain.
Misalnya, membandingkan bentuk gelombang tegangan dengan bentuk gelombang arus. Ini kemudian menghasilkan pergeseran sudut atau beda fasa antara dua bentuk gelombang sinusoidal. Setiap gelombang sinus yang tidak melewati nol pada t = 0 memiliki pergeseran fasa.
Beda fasa atau pergeseran fasa sebagaimana juga disebut sebagai Bentuk Gelombang Sinusoidal adalah sudut Φ (huruf Yunani Phi), dalam derajat atau radian yang bentuk gelombangnya telah bergeser dari titik referensi tertentu sepanjang sumbu nol horisontal. Dengan kata lain pergeseran fasa adalah Beda lateral antara dua atau lebih bentuk gelombang sepanjang sumbu umum dan bentuk gelombang sinusoidal dari frekuensi yang sama dapat memiliki beda fasa.
Beda fasa, Φ dari gelombang bolak-balik dapat bervariasi dari antara 0 hingga periode waktu maksimumnya, T dari gelombang selama satu siklus lengkap dan ini dapat di mana saja di sepanjang sumbu horizontal antara, Φ = 0 hingga 2π (radian) atau Φ = 0 hingga 360° tergantung pada unit sudut yang digunakan.
Beda fasa juga dapat dinyatakan sebagai pergeseran waktu dari τ di detik mewakili sebagian kecil dari periode waktu, T misalnya, + 10mS atau - 50US tetapi umumnya itu lebih umum untuk menyatakan Beda fasa sebagai pengukuran sudut. Maka persamaan untuk nilai sesaat dari tegangan sinusoidal atau bentuk gelombang arus yang kami kembangkan dalam bentuk gelombang Sinusoidal sebelumnya perlu dimodifikasi untuk memperhitungkan sudut fasa bentuk gelombang dan ekspresi umum baru ini menjadi.
Persamaan Beda Fasa
A(t) = Amax x sin (ωt ± Φ)Dimana:
Am -adalah amplitudo gelombang.
ωt - adalah frekuensi sudut dari bentuk gelombang dalam radian / detik.
Φ(phi) - adalah sudut fasa dalam derajat atau radian bahwa gelombang telah bergeser ke kiri atau kanan dari titik referensi.
Jika kemiringan positif dari bentuk gelombang sinusoidal melewati sumbu horizontal "sebelum" t = 0 maka bentuk gelombang telah bergeser ke kiri sehingga Φ>0, dan sudut fasa akan bersifat positif, +Φ memberikan sudut fasa terkemuka. Dengan kata lain itu muncul lebih awal daripada 0° menghasilkan rotasi berlawanan arah jarum jam dari vektor.
Demikian juga, jika kemiringan positif dari gelombang sinusoidal melewati horisontal sumbu x beberapa waktu “setelah” t = 0 maka gelombang telah bergeser ke kanan sehingga Φ<0, dan sudut fasa akan bersifat negatif -Φ menghasilkan sudut fasa lagging (tertinggal) seperti yang muncul kemudian dalam waktu dari 0° menghasilkan rotasi searah jarum jam vektor. Kedua kasus ditunjukkan di bawah ini.
Hubungan Fasa Bentuk Gelombang Sinusoidal

Pertama, mari kita perhatikan bahwa dua kuantitas bolak-balik seperti tegangan, v dan arus, i memiliki frekuensi yang sama f di Hertz. Karena frekuensi dua kuantitas adalah sama dengan kecepatan sudut, ω juga harus sama. Jadi kapan saja kita dapat mengatakan bahwa fasa tegangan, v akan sama dengan fasa arus, i. Maka sudut rotasi dalam periode waktu tertentu akan selalu sama dan beda fasa antara dua jumlah v dan i karena itu akan menjadi nol dan Φ = 0.
Sebagai frekuensi tegangan, v dan arus, i adalah sama mereka harus mencapai nilai positif, negatif dan nol maksimum selama satu siklus penuh pada waktu yang sama (walaupun amplitudo mereka mungkin berbeda). Kemudian dua kuantitas bolak-balik, v dan i dikatakan "dalam-fasa".
Dua Bentuk Gelombang Sinusoidal - “dalam fasa”

Sekarang mari kita perhatikan bahwa tegangan, v dan arus, i memiliki beda fasa antara mereka sendiri 30°, jadi (Φ = 30° atau π/6 radian). Karena kedua kuantitas bolak-balik berputar pada kecepatan yang sama, yaitu mereka memiliki frekuensi yang sama, beda fasa ini akan tetap konstan untuk semua instance dalam waktu, maka beda fasa 30° antara dua kuantitas diwakili oleh phi, Φ seperti yang ditunjukkan di bawah ini.
Beda Fasa Gelombang Sinusoidal

Bentuk gelombang tegangan di atas dimulai dari nol di sepanjang sumbu referensi horisontal, tetapi pada saat yang bersamaan, bentuk gelombang arus masih bernilai negatif dan tidak melewati sumbu referensi ini sampai 30° selanjutnya. Kemudian pada Beda Fasa antara kedua bentuk gelombang saat arus melintasi sumbu referensi horisontal mencapai puncak maksimum dan nilai nol setelah bentuk gelombang tegangan.
Karena dua bentuk gelombang tidak lagi "dalam-fasa", oleh karena itu mereka harus "keluar-fasa" dengan jumlah yang ditentukan oleh phi, Φ dan dalam contoh kita ini adalah 30°. Jadi kita dapat mengatakan bahwa dua bentuk gelombang sekarang 30° di luar fasa.
Bentuk gelombang arus juga bisa dikatakan "tertinggal" di belakang bentuk gelombang tegangan oleh sudut fasa, Φ. Kemudian dalam contoh kami di atas dua bentuk gelombang memiliki Beda Fasa Tertinggal sehingga ekspresi untuk tegangan dan arus di atas akan diberikan sebagai.
Tegangan (vt) = Vm sinωt
Arus (it) = Im sin (ωt-θ)
di mana, i Tertinggal v dengan sudut Φ
Demikian juga, jika arus, i memiliki nilai positif dan melintasi sumbu referensi mencapai puncak maksimum dan nilai nol pada beberapa waktu sebelum tegangan, v maka bentuk gelombang arus akan "memimpin" tegangan dengan beberapa sudut fasa. Kemudian kedua bentuk gelombang tersebut dikatakan memiliki Beda Fasa Terkemuka dan ekspresi untuk tegangan dan arus akan.
Tegangan (vt) = Vm sinωt
Arus (it) = Im sin (ωt+θ)
di mana, i Memimpin v dengan sudut Φ
Sudut fasa gelombang sinus dapat digunakan untuk menggambarkan hubungan satu gelombang sinus dengan yang lain dengan menggunakan istilah "Leading/memimpin" dan "Lagging/tertinggal" untuk menunjukkan hubungan antara dua bentuk gelombang sinusoidal dari frekuensi yang sama, diplot ke sumbu referensi yang sama.
Dalam contoh di atas dua bentuk gelombang yang diluar fasa dengan 30°. Jadi kita dapat dengan benar mengatakan bahwa i tertinggal v atau kita dapat mengatakan bahwa v memimpin i sampai 30° tergantung pada yang kita pilih sebagai referensi kita.
Hubungan antara kedua bentuk gelombang dan sudut fasa yang dihasilkan dapat diukur di mana saja di sepanjang sumbu nol horizontal yang dilalui setiap gelombang dengan arah "kemiringan yang sama" baik positif atau negatif.
Dalam rangkaian daya AC kemampuan ini untuk menggambarkan hubungan antara tegangan dan gelombang sinus arus dalam rangkaian yang sama sangat penting dan membentuk dasar analisis rangkaian AC.
Gelombang Cosinus (Cosine)
Jadi kita sekarang tahu bahwa jika gelombang adalah “bergeser” ke kanan atau kiri 0° bila dibandingkan dengan gelombang sinus lain ekspresi untuk gelombang ini menjadi Am sin (ωt ± Φ). Tetapi jika bentuk gelombang melintasi sumbu nol horisontal dengan kemiringan positif 90° atau rad/2 radian sebelum bentuk gelombang referensi, bentuk gelombang tersebut disebut Bentuk Gelombang Cosinus dan ekspresi menjadi.Ekspresi Cosinus
Gelombang Cosinus, biasanya hanya disebut “cos”, adalah sama pentingnya dengan gelombang sinus di bidang teknik listrik. Gelombang cosinus memiliki bentuk yang sama dengan gelombang sinus yang merupakan fungsi sinusoidal, tetapi digeser oleh +90° atau seperempat penuh periode di depannya.
Beda Fasa antara gelombang Sinus dan Cosinus

Atau, kita juga dapat mengatakan bahwa gelombang sinus adalah gelombang cosinus yang telah bergeser ke arah lain oleh -90°. Bagaimanapun juga ketika berhadapan dengan gelombang sinus atau gelombang cosinus dengan sudut aturan berikut akan selalu berlaku.
Hubungan Gelombang Sinus dan Cosinus
cos (ωt + ф) = sin(ωt + ф + 90°)sin (ωt + ф) = cos(ωt + ф - 90°)
Ketika membandingkan dua bentuk gelombang sinusoidal, lebih umum untuk mengekspresikan hubungan mereka sebagai sinus atau cosinus dengan amplitudo positif dan ini dicapai dengan menggunakan rumus matematika berikut.
-sin (ωt) = sin(ωt ± 180°)
-cos (ωt) = cos(ωt ± 180°)
-cos (ωt) = sin(ωt ± 270°)
±sin (ωt) = cos(ωt ± 90°)
±cos (ωt) = sin(ωt ± 90°)
-sin (ωt) = sin(-ωt)
cos (ωt) = cos(-ωt)
Dengan menggunakan hubungan-hubungan di atas, kita dapat mengubah bentuk gelombang sinusoidal dengan atau tanpa beda sudut atau fasa dari salah satu gelombang sinus menjadi gelombang cosinus atau sebaliknya.
Dalam tutorial berikutnya tentang Fasor kita akan menggunakan metode grafis untuk mewakili atau membandingkan beda fasa antara dua sinusoidal dengan melihat representasi fasor kuantitas AC fasa tunggal bersama dengan beberapa aljabar fasor yang berkaitan dengan penambahan matematis dua atau lebih fasor.
