Segitiga Daya
Daya listrik yang dikonsumsi dalam rangkaian AC dapat diwakili oleh tiga sisi dari segitiga siku-siku, yang umumnya dikenal sebagai segitiga daya
Kami melihat dalam tutorial kami tentang Daya Listrik bahwa rangkaian AC yang mengandung resistansi dan kapasitansi atau resistansi dan induktansi, atau keduanya, juga mengandung daya nyata dan daya reaktif.
Jadi agar kita dapat menghitung total daya yang dikonsumsi, kita perlu mengetahui perbedaan fasa antara bentuk gelombang sinusoidal dari tegangan dan arus.
Dalam rangkaian AC, bentuk gelombang tegangan dan arus adalah gelombang sinusoidal sehingga amplitudonya terus berubah seiring waktu. Karena kita tahu bahwa daya adalah tegangan kali arus (P = V*I), daya maksimum akan terjadi ketika dua tegangan dan bentuk gelombang arus disatukan satu sama lain.
Artinya, puncak dan titik nol crossover mereka terjadi pada saat yang sama. Ketika ini terjadi dua bentuk gelombang dikatakan "dalam-fasa".
Tiga komponen utama dalam rangkaian AC yang dapat mempengaruhi hubungan antara tegangan dan bentuk gelombang arus, dan oleh karena itu perbedaan fasa mereka, dengan mendefinisikan impedansi total rangkaian adalah Resistor, Kapasitor dan Induktor.
Impedansi, (Z) dari rangkaian AC setara dengan resistansi yang dihitung dalam rangkaian DC, dengan impedansi yang diberikan dalam ohm. Untuk rangkaian AC, impedansi umumnya didefinisikan sebagai rasio tegangan dan fasor arus yang dihasilkan oleh komponen rangkaian.
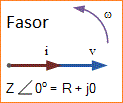
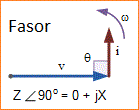
Fasor adalah garis lurus yang digambar sedemikian rupa untuk merepresentasikan tegangan atau amplitudo arus berdasarkan panjangnya dan perbedaan fasanya sehubungan dengan garis fasor lainnya dengan posisi sudut relatif terhadap fasor lainnya.
Rangkaian AC mengandung resistansi dan reaktansi yang digabungkan bersama untuk memberikan impedansi total (Z) yang membatasi aliran arus di sekitar rangkaian.
Tetapi impedansi rangkaian AC tidak sama dengan jumlah aljabar dari nilai-nilai ohm resistif dan reaktif karena resistansi murni dan reaktansi murni adalah 90° diluar-fasa dengan satu sama lain.
Tetapi kita dapat menggunakan perbedaan fasa 90° ini sebagai sisi-sisi dari segitiga siku-siku, yang disebut segitiga impedansi, dengan impedansi yang merupakan sisi miring yang ditentukan oleh teorema Pythagoras.
Hubungan geometris antara resistansi, reaktansi, dan impedansi dapat direpresentasikan secara visual dengan menggunakan segitiga impedansi seperti yang ditunjukkan.
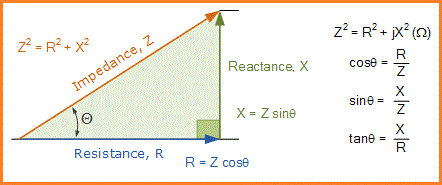
Perhatikan bahwa Impedansi, yang merupakan penjumlahan vektor dari resistansi dan reaktansi, tidak hanya memiliki besaran (Z) tetapi juga memiliki sudut fasa (θ), yang mewakili perbedaan fasa antara resistansi dan reaktansi.
Perhatikan juga bahwa segitiga akan berubah bentuk karena variasi dalam reaktansi, (X) ketika frekuensi berubah. Tentu saja, resistansi (R) akan selalu tetap konstan.
Kita dapat mengambil ide ini selangkah lebih maju dengan mengubah segitiga impedansi menjadi segitiga daya yang mewakili tiga elemen daya dalam rangkaian AC.
Hukum Ohm memberi tahu kita bahwa dalam rangkaian DC, daya (P), dalam watt, sama dengan kuadrat arus (I2) kali resistansi (R). Jadi kita dapat melipat-gandakan tiga sisi dari segitiga impedansi kita di atas dengan I2 untuk mendapatkan segitiga daya yang sesuai sebagai:
Daya Nyata P = I2R Watt, (W)
Daya Reaktif Q = I2X Volt-ampere Reaktif, (VAr)
Daya Semu S = I2Z Volt-ampere, (VA)
Maka daya, (P) dalam rangkaian AC sama dengan daya, P dalam rangkaian DC. Jadi sama seperti rangkaian DC, selalu dihitung sebagai I2*R, di mana R adalah komponen resistif total dari rangkaian.
Karena resistansi tidak menghasilkan perbedaan fasor (pergeseran fasa) antara tegangan dan bentuk gelombang arus, semua daya yang berguna dikirim langsung ke resistansi dan dikonversi menjadi panas, cahaya dan pekerjaan.
Maka daya yang dikonsumsi oleh sebuah resistansi/perlawanan adalah daya nyata yang pada dasarnya adalah daya rata-rata rangkaian.
Untuk menemukan nilai daya nyata yang sesuai, nilai tegangan dan arus rms dikalikan dengan kosinus sudut fasa, θ seperti yang ditunjukkan.
Daya Nyata P = I2R = V*I*cos (θ) Watts, (W)
Tetapi karena tidak ada perbedaan fasa antara tegangan dan arus dalam rangkaian resistif, pergeseran fasa antara kedua bentuk gelombang akan menjadi nol (0). Kemudian:
cos(0°) = 1
P = Vrms x Irms x 1
∴P = Vrms x Irms (watt)
Di mana daya (P) dalam watt, tegangan (V) dalam volt rms dan arus (I) dalam ampere rms.
Maka daya sesungguhnya adalah elemen resistif I2*R yang diukur dalam watt, yang adalah apa yang Anda baca pada meter energi utilitas Anda dan memiliki satuan dalam Watt (W), Kilowatts (kW), dan Megawatt (MW). Perhatikan bahwa daya nyata, P selalu positif.
Daya reaktif terkait dengan reaktansi yang dihasilkan oleh induktor dan kapasitor dan menetralkan efek daya nyata. Daya reaktif tidak ada di rangkaian DC.
Tidak seperti daya nyata (P) yang melakukan semua pekerjaan, daya reaktif (Q) mengambil daya dari rangkaian karena penciptaan dan pengurangan medan magnet induktif dan medan elektrostatis kapasitif, sehingga mempersulit daya sebenarnya untuk memasok daya langsung ke rangkaian atau beban.
Daya yang disimpan oleh induktor dalam medan magnetnya mencoba mengendalikan arus, sedangkan daya yang disimpan oleh medan elektrostatis kapasitor mencoba mengendalikan tegangan.
Hasilnya adalah kapasitor “menghasilkan” daya reaktif dan induktor “mengonsumsi” daya reaktif. Ini berarti bahwa keduanya mengkonsumsi dan mengembalikan daya ke sumber sehingga tidak ada daya nyata yang dikonsumsi.
Untuk menemukan daya reaktif, tegangan rms dan nilai arus dikalikan dengan sinus sudut fasa, θ seperti yang ditunjukkan.
Daya Reaktif Q = I2X = V * I * sin (θ) volt-ampere reaktif, (VAr)
Karena ada perbedaan fasa 90° antara tegangan dan bentuk gelombang arus dalam reaktansi murni (baik induktif atau kapasitif), mengalikan V*I dengan sin (θ) memberikan komponen vertikal yang 90° diluar-fasa dengan masing-masing lainnya, jadi:
cos(90°) = 1
Q = Vrms x Irms x 1
∴Q = Vrms x Irms (VAr)
Di mana daya reaktif (Q) dalam volt-ampere reaktif, tegangan (V) ada di volt rms dan arus (I) ada di rms ampere.
Kemudian daya reaktif mewakili hasil volt dan ampere yang berada diluar-fasa 90° satu sama lain, tetapi secara umum, bisa ada sudut fasa, θ antara tegangan dan arus.
Dengan demikian daya reaktif adalah elemen reaktif I2X yang memiliki satuan reaktif volt-ampere (VAr), Kilovolt-ampere reaktif (kVAr), dan Megavolt-ampere reaktif (MVAr).
Kemudian ada hubungan matematis antara daya nyata (P), dan daya reaktif (Q), yang disebut daya kompleks. Hasil dari tegangan rms, V diterapkan pada rangkaian AC dan arus rms, I mengalir ke rangkaian itu disebut "volt-ampere" (VA) diberi simbol S dan yang besarnya dikenal umumnya sebagai daya semu.
Daya kompleks ini tidak sama dengan jumlah aljabar dari daya nyata dan reaktif yang ditambahkan bersama-sama, tetapi sebaliknya adalah jumlah vektor dari P dan Q yang diberikan dalam volt-amp (VA).
Ini adalah daya kompleks yang diwakili oleh segitiga daya. Nilai rms dari hasil volt-ampere dikenal lebih umum sebagai daya semu, “Apparent” ini adalah daya total yang dikonsumsi oleh suatu rangkaian walaupun daya sesungguhnya yang bekerja jauh lebih sedikit.
Karena daya semu terdiri dari dua bagian, daya resistif yang merupakan daya dalam-fasa atau daya nyata dalam watt dan daya reaktif yang merupakan daya luar-fasa dalam volt-ampere, kita dapat menunjukkan penambahan vektor dari dua komponen daya ini dalam bentuk segitiga daya. Segitiga daya memiliki empat bagian: P, Q, S dan θ.
Tiga elemen yang membentuk daya dalam rangkaian AC dapat diwakili secara grafis oleh tiga sisi dari segitiga siku-siku, dalam banyak cara yang sama dengan segitiga impedansi sebelumnya.
Sisi horisontal (berdekatan) mewakili rangkaian daya nyata (P), sisi vertikal (berlawanan) mewakili rangkaian daya reaktif (Q) dan sisi miring mewakili daya semu yang dihasilkan (S), dari segitiga daya seperti yang ditunjukkan.
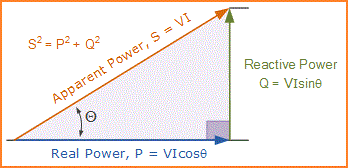
Dimana:
P adalah I2*R atau daya Real/Nyata yang melakukan pekerjaan yang diukur dalam watt, W
Q adalah I2*X atau daya Reaktif yang diukur dalam volt-ampere reaktif, VAr
S adalah I2*Z atau daya Apparent/Semu yang diukur dalam volt-ampere, VA
θ adalah sudut fasa dalam derajat. Semakin besar sudut fasa, semakin besar daya reaktif
Cos (θ) = P / S = W / VA = faktor daya, hal
Dosa (θ) = Q / S = VAr / VA
Tan (Ar) = Q / P = VAr / W
Faktor daya dihitung sebagai rasio daya nyata terhadap daya semu karena rasio ini sama dengan cos (θ).
Belitan coil yang memiliki induktansi 180mH dan resistansi 35Ω terhubung ke catu 100V 50Hz. Hitung: a) impedansi coil, b) arus, c) faktor daya, dan d) daya semu yang dikonsumsi.
Juga gambar segitiga daya yang dihasilkan untuk coil di atas.
Data yang diberikan: R = 35Ω, L = 180mH, V = 100V dan ƒ = 50Hz.
(a) Impedansi (Z) dari coil:
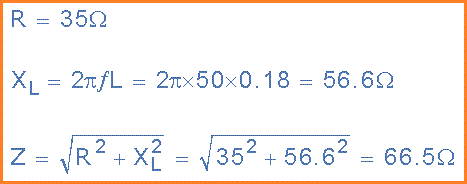
(b) Arus (I) dikonsumsi oleh coil:
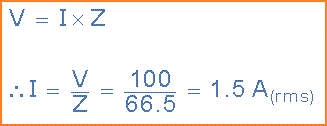
(c) Faktor daya dan sudut fasa, θ :
(d) Daya semu (S) dikonsumsi oleh coil:
(e) Segitiga daya untuk coil:
Seperti yang ditunjukkan oleh hubungan segitiga daya pada contoh sederhana ini, pada faktor daya 0.5263 atau 52.63%, coil membutuhkan daya 150 VA untuk menghasilkan 79 Watt pekerjaan yang bermanfaat.
Dengan kata lain, pada faktor daya 52.63%, coil membutuhkan sekitar 89% lebih banyak arus untuk melakukan pekerjaan yang sama, yang merupakan banyak arus terbuang.
Karena ketiga elemen ini diwakili oleh "segitiga siku-siku", hubungan mereka dapat didefinisikan sebagai: S2 = P2 + Q2 , di mana: P adalah daya nyata dalam watt (W), Q adalah daya reaktif dalam volt-ampere reaktif (VAr) dan S adalah daya semu dalam volt-ampere (VA).
Pada tutorial selanjutnya tentang Rangkaian AC kita akan membahas lebih tentang Faktor Daya yang juga bagian penting dari rangkaian AC yang juga dapat dinyatakan dalam rangkaian impedansi rangkaian atau daya rangkaian
Kami melihat dalam tutorial kami tentang Daya Listrik bahwa rangkaian AC yang mengandung resistansi dan kapasitansi atau resistansi dan induktansi, atau keduanya, juga mengandung daya nyata dan daya reaktif.
Jadi agar kita dapat menghitung total daya yang dikonsumsi, kita perlu mengetahui perbedaan fasa antara bentuk gelombang sinusoidal dari tegangan dan arus.
Dalam rangkaian AC, bentuk gelombang tegangan dan arus adalah gelombang sinusoidal sehingga amplitudonya terus berubah seiring waktu. Karena kita tahu bahwa daya adalah tegangan kali arus (P = V*I), daya maksimum akan terjadi ketika dua tegangan dan bentuk gelombang arus disatukan satu sama lain.
Artinya, puncak dan titik nol crossover mereka terjadi pada saat yang sama. Ketika ini terjadi dua bentuk gelombang dikatakan "dalam-fasa".
Tiga komponen utama dalam rangkaian AC yang dapat mempengaruhi hubungan antara tegangan dan bentuk gelombang arus, dan oleh karena itu perbedaan fasa mereka, dengan mendefinisikan impedansi total rangkaian adalah Resistor, Kapasitor dan Induktor.
Impedansi, (Z) dari rangkaian AC setara dengan resistansi yang dihitung dalam rangkaian DC, dengan impedansi yang diberikan dalam ohm. Untuk rangkaian AC, impedansi umumnya didefinisikan sebagai rasio tegangan dan fasor arus yang dihasilkan oleh komponen rangkaian.
Fasor adalah garis lurus yang digambar sedemikian rupa untuk merepresentasikan tegangan atau amplitudo arus berdasarkan panjangnya dan perbedaan fasanya sehubungan dengan garis fasor lainnya dengan posisi sudut relatif terhadap fasor lainnya.
Rangkaian AC mengandung resistansi dan reaktansi yang digabungkan bersama untuk memberikan impedansi total (Z) yang membatasi aliran arus di sekitar rangkaian.
Tetapi impedansi rangkaian AC tidak sama dengan jumlah aljabar dari nilai-nilai ohm resistif dan reaktif karena resistansi murni dan reaktansi murni adalah 90° diluar-fasa dengan satu sama lain.
Tetapi kita dapat menggunakan perbedaan fasa 90° ini sebagai sisi-sisi dari segitiga siku-siku, yang disebut segitiga impedansi, dengan impedansi yang merupakan sisi miring yang ditentukan oleh teorema Pythagoras.
Hubungan geometris antara resistansi, reaktansi, dan impedansi dapat direpresentasikan secara visual dengan menggunakan segitiga impedansi seperti yang ditunjukkan.
Segitiga Impedansi
Perhatikan bahwa Impedansi, yang merupakan penjumlahan vektor dari resistansi dan reaktansi, tidak hanya memiliki besaran (Z) tetapi juga memiliki sudut fasa (θ), yang mewakili perbedaan fasa antara resistansi dan reaktansi.
Perhatikan juga bahwa segitiga akan berubah bentuk karena variasi dalam reaktansi, (X) ketika frekuensi berubah. Tentu saja, resistansi (R) akan selalu tetap konstan.
Kita dapat mengambil ide ini selangkah lebih maju dengan mengubah segitiga impedansi menjadi segitiga daya yang mewakili tiga elemen daya dalam rangkaian AC.
Hukum Ohm memberi tahu kita bahwa dalam rangkaian DC, daya (P), dalam watt, sama dengan kuadrat arus (I2) kali resistansi (R). Jadi kita dapat melipat-gandakan tiga sisi dari segitiga impedansi kita di atas dengan I2 untuk mendapatkan segitiga daya yang sesuai sebagai:
Daya Nyata P = I2R Watt, (W)
Daya Reaktif Q = I2X Volt-ampere Reaktif, (VAr)
Daya Semu S = I2Z Volt-ampere, (VA)
Daya Nyata di Rangkaian AC
Daya (P - power), juga dikenal sebagai daya nyata atau aktif, melakukan "pekerjaan nyata" dalam rangkaian listrik. Daya nyata, diukur dalam watt, mendefinisikan daya yang dikonsumsi oleh bagian resistif dari sebuah rangkaian.Maka daya, (P) dalam rangkaian AC sama dengan daya, P dalam rangkaian DC. Jadi sama seperti rangkaian DC, selalu dihitung sebagai I2*R, di mana R adalah komponen resistif total dari rangkaian.
Karena resistansi tidak menghasilkan perbedaan fasor (pergeseran fasa) antara tegangan dan bentuk gelombang arus, semua daya yang berguna dikirim langsung ke resistansi dan dikonversi menjadi panas, cahaya dan pekerjaan.
Maka daya yang dikonsumsi oleh sebuah resistansi/perlawanan adalah daya nyata yang pada dasarnya adalah daya rata-rata rangkaian.
Untuk menemukan nilai daya nyata yang sesuai, nilai tegangan dan arus rms dikalikan dengan kosinus sudut fasa, θ seperti yang ditunjukkan.
Daya Nyata P = I2R = V*I*cos (θ) Watts, (W)
Tetapi karena tidak ada perbedaan fasa antara tegangan dan arus dalam rangkaian resistif, pergeseran fasa antara kedua bentuk gelombang akan menjadi nol (0). Kemudian:
Daya Nyata di Rangkaian AC
P = Vrms x Irms x cosθcos(0°) = 1
P = Vrms x Irms x 1
∴P = Vrms x Irms (watt)
Di mana daya (P) dalam watt, tegangan (V) dalam volt rms dan arus (I) dalam ampere rms.
Maka daya sesungguhnya adalah elemen resistif I2*R yang diukur dalam watt, yang adalah apa yang Anda baca pada meter energi utilitas Anda dan memiliki satuan dalam Watt (W), Kilowatts (kW), dan Megawatt (MW). Perhatikan bahwa daya nyata, P selalu positif.
Daya Reaktif di Rangkaian AC
Daya reaktif (Q), (kadang-kadang disebut daya tanpa watt) adalah daya yang dikonsumsi dalam rangkaian AC yang tidak melakukan pekerjaan yang bermanfaat tetapi memiliki efek besar pada pergeseran fasa antara tegangan dan bentuk gelombang arus.Daya reaktif terkait dengan reaktansi yang dihasilkan oleh induktor dan kapasitor dan menetralkan efek daya nyata. Daya reaktif tidak ada di rangkaian DC.
Daya yang disimpan oleh induktor dalam medan magnetnya mencoba mengendalikan arus, sedangkan daya yang disimpan oleh medan elektrostatis kapasitor mencoba mengendalikan tegangan.
Hasilnya adalah kapasitor “menghasilkan” daya reaktif dan induktor “mengonsumsi” daya reaktif. Ini berarti bahwa keduanya mengkonsumsi dan mengembalikan daya ke sumber sehingga tidak ada daya nyata yang dikonsumsi.
Untuk menemukan daya reaktif, tegangan rms dan nilai arus dikalikan dengan sinus sudut fasa, θ seperti yang ditunjukkan.
Daya Reaktif Q = I2X = V * I * sin (θ) volt-ampere reaktif, (VAr)
Karena ada perbedaan fasa 90° antara tegangan dan bentuk gelombang arus dalam reaktansi murni (baik induktif atau kapasitif), mengalikan V*I dengan sin (θ) memberikan komponen vertikal yang 90° diluar-fasa dengan masing-masing lainnya, jadi:
Daya Reaktif dalam Rangkaian AC
Q = Vrms x Irms x sinθcos(90°) = 1
Q = Vrms x Irms x 1
∴Q = Vrms x Irms (VAr)
Di mana daya reaktif (Q) dalam volt-ampere reaktif, tegangan (V) ada di volt rms dan arus (I) ada di rms ampere.
Kemudian daya reaktif mewakili hasil volt dan ampere yang berada diluar-fasa 90° satu sama lain, tetapi secara umum, bisa ada sudut fasa, θ antara tegangan dan arus.
Dengan demikian daya reaktif adalah elemen reaktif I2X yang memiliki satuan reaktif volt-ampere (VAr), Kilovolt-ampere reaktif (kVAr), dan Megavolt-ampere reaktif (MVAr).
Daya Semu di Rangkaian AC
Kita telah melihat di atas bahwa daya nyata dihamburkan oleh resistansi/perlawanan dan bahwa daya reaktif disuplai ke reaktansi. Sebagai akibatnya, bentuk gelombang arus dan tegangan tidak dalam fasa karena perbedaan antara komponen resistif rangkaian dan reaktif.Kemudian ada hubungan matematis antara daya nyata (P), dan daya reaktif (Q), yang disebut daya kompleks. Hasil dari tegangan rms, V diterapkan pada rangkaian AC dan arus rms, I mengalir ke rangkaian itu disebut "volt-ampere" (VA) diberi simbol S dan yang besarnya dikenal umumnya sebagai daya semu.
Daya kompleks ini tidak sama dengan jumlah aljabar dari daya nyata dan reaktif yang ditambahkan bersama-sama, tetapi sebaliknya adalah jumlah vektor dari P dan Q yang diberikan dalam volt-amp (VA).
Ini adalah daya kompleks yang diwakili oleh segitiga daya. Nilai rms dari hasil volt-ampere dikenal lebih umum sebagai daya semu, “Apparent” ini adalah daya total yang dikonsumsi oleh suatu rangkaian walaupun daya sesungguhnya yang bekerja jauh lebih sedikit.
Karena daya semu terdiri dari dua bagian, daya resistif yang merupakan daya dalam-fasa atau daya nyata dalam watt dan daya reaktif yang merupakan daya luar-fasa dalam volt-ampere, kita dapat menunjukkan penambahan vektor dari dua komponen daya ini dalam bentuk segitiga daya. Segitiga daya memiliki empat bagian: P, Q, S dan θ.
Tiga elemen yang membentuk daya dalam rangkaian AC dapat diwakili secara grafis oleh tiga sisi dari segitiga siku-siku, dalam banyak cara yang sama dengan segitiga impedansi sebelumnya.
Sisi horisontal (berdekatan) mewakili rangkaian daya nyata (P), sisi vertikal (berlawanan) mewakili rangkaian daya reaktif (Q) dan sisi miring mewakili daya semu yang dihasilkan (S), dari segitiga daya seperti yang ditunjukkan.
Segitiga Daya dari Rangkaian AC
Dimana:
P adalah I2*R atau daya Real/Nyata yang melakukan pekerjaan yang diukur dalam watt, W
Q adalah I2*X atau daya Reaktif yang diukur dalam volt-ampere reaktif, VAr
S adalah I2*Z atau daya Apparent/Semu yang diukur dalam volt-ampere, VA
θ adalah sudut fasa dalam derajat. Semakin besar sudut fasa, semakin besar daya reaktif
Cos (θ) = P / S = W / VA = faktor daya, hal
Dosa (θ) = Q / S = VAr / VA
Tan (Ar) = Q / P = VAr / W
Faktor daya dihitung sebagai rasio daya nyata terhadap daya semu karena rasio ini sama dengan cos (θ).
Contoh: Segitiga Daya (Power Triangle) No.1
Juga gambar segitiga daya yang dihasilkan untuk coil di atas.
Data yang diberikan: R = 35Ω, L = 180mH, V = 100V dan ƒ = 50Hz.
(a) Impedansi (Z) dari coil:
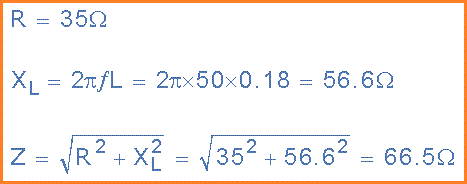
(b) Arus (I) dikonsumsi oleh coil:
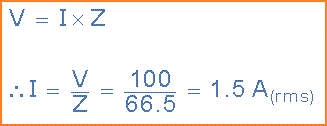
(c) Faktor daya dan sudut fasa, θ :
(d) Daya semu (S) dikonsumsi oleh coil:
(e) Segitiga daya untuk coil:
Seperti yang ditunjukkan oleh hubungan segitiga daya pada contoh sederhana ini, pada faktor daya 0.5263 atau 52.63%, coil membutuhkan daya 150 VA untuk menghasilkan 79 Watt pekerjaan yang bermanfaat.
Dengan kata lain, pada faktor daya 52.63%, coil membutuhkan sekitar 89% lebih banyak arus untuk melakukan pekerjaan yang sama, yang merupakan banyak arus terbuang.
Ringkasan Segitiga Daya
Kita telah melihat di sini bahwa tiga unsur daya listrik, Daya Nyata (real), Daya Reaktif dan Daya Semu (apparent) dalam sebuah rangkaian AC dapat diwakili oleh tiga sisi segitiga yang disebut Segitiga Daya.Karena ketiga elemen ini diwakili oleh "segitiga siku-siku", hubungan mereka dapat didefinisikan sebagai: S2 = P2 + Q2 , di mana: P adalah daya nyata dalam watt (W), Q adalah daya reaktif dalam volt-ampere reaktif (VAr) dan S adalah daya semu dalam volt-ampere (VA).
Pada tutorial selanjutnya tentang Rangkaian AC kita akan membahas lebih tentang Faktor Daya yang juga bagian penting dari rangkaian AC yang juga dapat dinyatakan dalam rangkaian impedansi rangkaian atau daya rangkaian