Rangkaian Resonansi RLC - Cara Kerja dan Aplikasi
Rangkaian RLC adalah rangkaian listrik yang terdiri dari Resistor, Induktor, dan Kapasitor yang diwakili oleh huruf R, L, dan C. Rangkaian resonansi RLC dihubungkan secara seri dan paralel. Nama Rangkaian RLC berasal dari huruf awal dari komponen Resistor, Induktor, dan Kapasitor. Untuk rangkaian tujuan saat ini arus membentuk osilator harmonik.
Menggunakan rangkaian LC dari resonansi. Jika resistor meningkat, ia menguraikan osilasi yang dikenal sebagai redaman. Beberapa resistansi sulit ditemukan dalam waktu nyata, bahkan setelah resistor tidak diidentifikasi sebagai komponen yang diselesaikan oleh rangkaian LC.
Di mana R adalah resistansi, J adalah unit imajiner dan X adalah reaktansi.
Ada pulsa yang ditandatangani antara R dan JX. Unit imajiner adalah resistansi luar. Energi yang tersimpan adalah komponen kapasitor dan induktor. Kapasitor disimpan di medan listrik dan induktor disimpan di medan magnitudo.
Dari persamaan Z = R + JK kita dapat mendefinisikan reaktansi sebagai
Nilai absolut dari reaktansi muatan induktor dan kapasitor dengan frekuensi seperti yang ditunjukkan pada gambar di bawah ini.
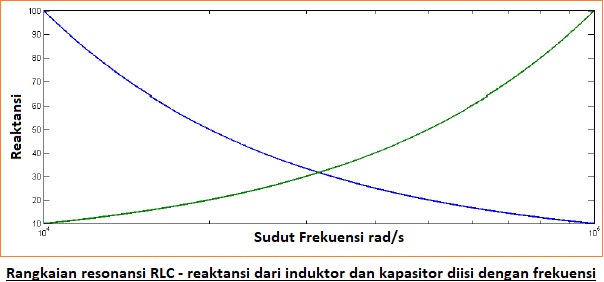
Q ( ω ) = energi daya maksimum yang tersimpan/kehilangan daya
Faktor Q bergantung pada frekuensi yang paling sering dikutip untuk frekuensi resonansi dan energi maksimum yang tersimpan dalam kapasitor dan dalam induktor dapat menghitung frekuensi resonansi yang disimpan dalam rangkaian resonansi. Persamaan yang relevan adalah
Energi maksimum yang disimpan = LI2Lrms = C V 2Crms
ILrms dilambangkan sebagai arus rms melalui induktor. Itu sama dengan total arus rms yang terbentuk di rangkaian dalam rangkaian seri dan di rangkaian paralel tidak sama. Demikian pula, dalam VCrms adalah tegangan melintasi kapasitor itu ditunjukkan dalam rangkaian paralel dan itu sama dengan tegangan supply rms tetapi dalam rangkaian seri disepakati oleh pembagi potensial.
Dengan demikian rangkaian rangkaian sederhana untuk menghitung energi maksimum yang disimpan melalui indikator dan dalam rangkaian paralelnya dipertimbangkan melalui kapasitor.
Daya nyata mengalami degenerasi pada resistor
P = VRrms IRrms = I2Rrms R = V2Rrms/R
Cara termudah untuk menemukan rangkaian RLC seri
Q(S)ω0 = ω0 I2rms L/I2rms R = ω0 L/R
Rangkaian RLC paralel adalah untuk mempertimbangkan tegangan
Q(P)ω0 = ω0 RCV2Crms /V2Crms = ω0 CR
Jika kita dapat menyambungkan kembali Xcis negatif, maka jelas bahwa XL + XC harus sama dengan nol untuk frekuensi spesifik ini XL = -X komponen impedansi imajiner secara persis membatalkan satu sama lain. Pada pergerakan frekuensi ini, impedansi rangkaian memiliki magnitudo rendah dan sudut fasa nol, disebut sebagai frekuensi resonansi rangkaian.
XL + XC = 0
XL = - XC = ω0 L = 1/ω0 C = 1/LC
ω0 = √1/LC ω0
= 2Π f0
Untuk nilai-nilai R, L, dan C rasio diplot terhadap frekuensi sudut dan gambar menunjukkan sifat-sifat amplifikasi. Frekuensi resonansi
VC/V- 1/j ω0 RC
VC/V- j ω0 L/R
Kita dapat melihat bahwa karena ini adalah rangkaian positif, jumlah daya yang dihabiskan adalah konstan
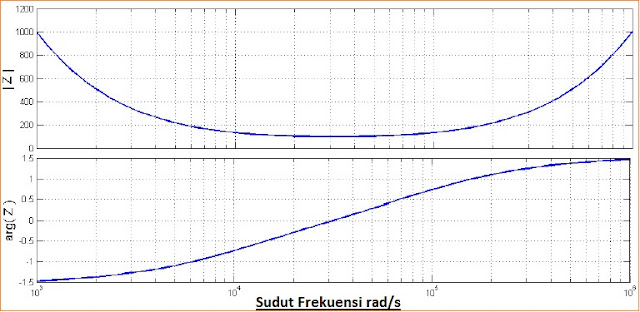
Ketika XC = - XL Puncak resonansi datang sekali lagi dan dengan demikian frekuensi resonansi memiliki hubungan yang sama.
Untuk menghitung gain arus dengan melihat arus di masing-masing lengan, maka gain kapasitor diberikan sebagai
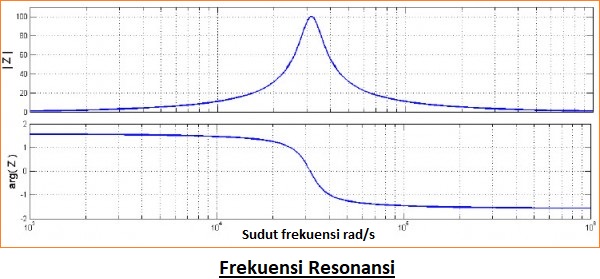
Gain arus magnitudo ditunjukkan pada gambar dan frekuensi resonansi
Menggunakan rangkaian LC dari resonansi. Jika resistor meningkat, ia menguraikan osilasi yang dikenal sebagai redaman. Beberapa resistansi sulit ditemukan dalam waktu nyata, bahkan setelah resistor tidak diidentifikasi sebagai komponen yang diselesaikan oleh rangkaian LC.
Rangkaian Resonansi RLC
Sementara berurusan dengan resonansi itu adalah komponen yang kompleks dan memiliki banyak perbedaan. Impedansi z dan rangkaiannya didefinisikan sebagai
Z = R + JX
Ada pulsa yang ditandatangani antara R dan JX. Unit imajiner adalah resistansi luar. Energi yang tersimpan adalah komponen kapasitor dan induktor. Kapasitor disimpan di medan listrik dan induktor disimpan di medan magnitudo.
ZC = 1/jωc
= -J/ωc
ZL = jωL
XC = -1/ωc
XL = ωL

Faktor Q
Singkatan Q didefinisikan sebagai kualitas dan juga dikenal sebagai faktor Kualitas. Faktor kualitas menjelaskan tentang resonator yang kurang teredam. Jika resonator kurang teredam meningkatkan faktor kualitas berkurang. Peredaman rangkaian resonator listrik menghasilkan hilangnya energi dalam komponen resistif. Ekspresi matematis dari faktor Q didefinisikan sebagaiQ ( ω ) = energi daya maksimum yang tersimpan/kehilangan daya
Faktor Q bergantung pada frekuensi yang paling sering dikutip untuk frekuensi resonansi dan energi maksimum yang tersimpan dalam kapasitor dan dalam induktor dapat menghitung frekuensi resonansi yang disimpan dalam rangkaian resonansi. Persamaan yang relevan adalah
Energi maksimum yang disimpan = LI2Lrms = C V 2Crms
ILrms dilambangkan sebagai arus rms melalui induktor. Itu sama dengan total arus rms yang terbentuk di rangkaian dalam rangkaian seri dan di rangkaian paralel tidak sama. Demikian pula, dalam VCrms adalah tegangan melintasi kapasitor itu ditunjukkan dalam rangkaian paralel dan itu sama dengan tegangan supply rms tetapi dalam rangkaian seri disepakati oleh pembagi potensial.
Dengan demikian rangkaian rangkaian sederhana untuk menghitung energi maksimum yang disimpan melalui indikator dan dalam rangkaian paralelnya dipertimbangkan melalui kapasitor.
Daya nyata mengalami degenerasi pada resistor
P = VRrms IRrms = I2Rrms R = V2Rrms/R
Cara termudah untuk menemukan rangkaian RLC seri
Q(S)ω0 = ω0 I2rms L/I2rms R = ω0 L/R
Rangkaian RLC paralel adalah untuk mempertimbangkan tegangan
Q(P)ω0 = ω0 RCV2Crms /V2Crms = ω0 CR
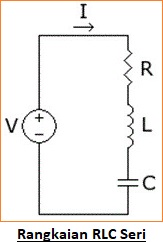
Rangkaian RLC Seri
Rangkaian RLC seri terdiri dari resistansi, induktor, dan kapasitor yang dihubungkan secara seri dalam rangkaian RLC seri. Diagram di bawah ini menunjukkan rangkaian RLC seri. Dalam rangkaian ini kapasitor dan induktor akan menggabungkan satu sama lain dan meningkatkan frekuensi.Jika kita dapat menyambungkan kembali Xcis negatif, maka jelas bahwa XL + XC harus sama dengan nol untuk frekuensi spesifik ini XL = -X komponen impedansi imajiner secara persis membatalkan satu sama lain. Pada pergerakan frekuensi ini, impedansi rangkaian memiliki magnitudo rendah dan sudut fasa nol, disebut sebagai frekuensi resonansi rangkaian.

XL + XC = 0
XL = - XC = ω0 L = 1/ω0 C = 1/LC
ω0 = √1/LC ω0
= 2Π f0
Rangkaian RLC Berubah-ubah
Kita dapat mengamati efek resonansi dengan mempertimbangkan tegangan melintasi komponen resistif ke tegangan input untuk contoh yang dapat kita pertimbangkan untuk kapasitor.
VC/V = 1/1-ω2 LC + j ωRC
VC/V- 1/j ω0 RC
VC/V- j ω0 L/R
Kita dapat melihat bahwa karena ini adalah rangkaian positif, jumlah daya yang dihabiskan adalah konstan

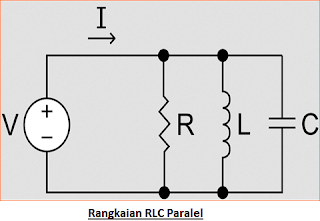
Rangkaian RLC Paralel
Dalam Rangkaian RLC paralel, komponen resistor, induktor, dan kapasitor dihubungkan secara paralel. Rangkaian resonansi RLC adalah rangkaian seri ganda dalam peran pertukaran tegangan dan arus. Oleh karena itu rangkaian memiliki gain arus daripada impedansi dan gain tegangan maksimum pada frekuensi resonansi atau diminimalkan. Impedansi total rangkaian diberikan sebagai
= R ‖ ZL ‖ ZC
= R/1- JR (1/XC + 1/XL)
= R/1+ JR (ωc - 1/ωL)
ω0 = √1/LC
ic/i = jωRC/1+ jR (ωc - 1/ωL)

ic/i = jRC
Aplikasi Rangkaian Resonansi RLC
Rangkaian resonansi RLC memiliki banyak aplikasi seperti:- Rangkaian Osilator, penerima radio, dan pesawat televisi digunakan untuk tujuan penyetelan.
- Rangkaian RLC Seri terutama terlibat dalam pemrosesan sinyal dan sistem komunikasi
- Rangkaian Resonansi LC Seri digunakan untuk menyediakan pembesaran tegangan
- Rangkaian LC seri dan paralel digunakan dalam pemanasan induksi