Reaktansi Induktif - Reaktansi dari Sebuah Induktor
Reaktansi induktif kumparan atau coil tergantung pada frekuensi tegangan yang diberikan karena reaktansi berbanding lurus dengan frekuensi.
Sejauh ini kita telah melihat perilaku Induktor yang terhubung ke supply DC dan mudah-mudahan sekarang kita tahu bahwa ketika tegangan DC diterapkan pada induktor, pertumbuhan arus melalui itu tidak instan tetapi ditentukan oleh induktor yang diinduksi sendiri atau nilai ggl-balik.
Kami juga melihat bahwa arus induktor terus naik hingga mencapai kondisi stabil maksimum setelah lima konstanta waktu. Arus maksimum mengalir melalui coil induktif hanya dibatasi oleh bagian resistif dari gulungan coil dalam Ohm, dan seperti yang kita tahu dari hukum Ohm, ini ditentukan oleh rasio tegangan terhadap arus, V/R.
Ketika tegangan AC atau bolak-balik diterapkan pada sebuah induktor, aliran arus yang melaluinya berperilaku sangat berbeda dengan tegangan DC yang diterapkan. Efek dari supply sinusoidal menghasilkan perbedaan fasa antara tegangan dan bentuk gelombang arus.
Sekarang di rangkaian AC, perlawanan terhadap aliran arus melalui gulungan coil tidak hanya tergantung pada induktansi coil tetapi juga frekuensi bentuk gelombang AC.
Perlawanan terhadap arus yang mengalir melalui coil di rangkaian AC ditentukan oleh resistansi AC, atau yang lebih dikenal sebagai Impedansi (Z), dari rangkaian.
Tetapi resistansi selalu dikaitkan dengan rangkaian DC sehingga untuk membedakan resistansi DC dari resistansi AC, istilah Reaktansi umumnya digunakan.
Sama seperti resistansi, nilai reaktansi juga diukur dalam Ohm tetapi diberi simbol X, (huruf besar "X"), untuk membedakannya dari nilai resistif murni.
Karena komponen yang kami bahas adalah induktor, maka reaktansi pada sebuah induktor disebut “Reaktansi Induktif”. Dengan kata lain, resistansi listrik induktor ketika digunakan dalam rangkaian AC disebut Reaktansi Induktif.
Reaktansi Induktif yang diberi simbol XL, adalah properti dalam rangkaian AC yang menentang perubahan arus. Dalam tutorial kami tentang Kapasitor dalam Rangkaian AC, kami melihat bahwa dalam rangkaian kapasitif murni, arus IC "MEMIMPIN" tegangan sebesar 90°. Dalam rangkaian AC murni induktif sebaliknya adalah benar, arus IL “TERTINGGAL” tegangan yang diberikan oleh 90°, atau (π/2 rad).

Dalam rangkaian induktif murni di atas, induktor terhubung langsung melintasi tegangan supply AC. Ketika tegangan supply meningkat dan menurun dengan frekuensi, ggl-balik yang diinduksi sendiri juga meningkat dan berkurang dalam coil sehubungan dengan perubahan ini.
Kita tahu bahwa ggl yang diinduksi sendiri ini berbanding lurus dengan laju perubahan arus melalui coil dan paling besar sebagai tegangan supply melintas dari setengah siklus positif ke setengah siklus negatif atau sebaliknya pada titik, 0° dan 180° sepanjang gelombang sinus.
Akibatnya, tingkat perubahan tegangan minimum terjadi ketika gelombang sinus AC melintasi pada level tegangan puncak maksimum atau minimum. Pada posisi ini dalam siklus, arus maksimum atau minimum mengalir melalui rangkaian induktor dan ini ditunjukkan di bawah ini.
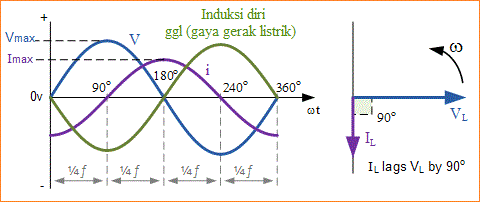
Tegangan dan arus gelombang ini menunjukkan bahwa untuk rangkaian induktif murni arus tertinggal tegangan sebesar 90°. Walaupun begitu, kita juga dapat mengatakan bahwa tegangan memimpin arus sebesar 90°.
Bagaimanapun juga ekspresi umum adalah bahwa arus tertinggal seperti yang ditunjukkan pada diagram vektor. Berikut vektor arus dan vektor tegangan ditampilkan displaced oleh 90°. Arus tertinggal dari tegangan.
Kami juga dapat menulis pernyataan ini sebagai, VL = 0° dan IL = -90° sehubungan dengan tegangan, VL. Jika bentuk gelombang tegangan digolongkan sebagai gelombang sinus maka arus, IL dapat digolongkan sebagai cosinus negatif dan kita dapat menentukan nilai arus pada titik waktu sebagai:
Di mana: ω dalam radian per detik dan t dalam detik (second).
Sejak arus tertinggal tegangan sebesar 90° di rangkaian induktif murni, kita dapat menemukan fasa arus dengan mengetahui fasa tegangan atau sebaliknya. Jadi jika kita tahu nilai VL, maka IL harus tertinggal sebesar 90°.
Demikian juga, jika kita tahu nilai IL maka VL karena itu harus memimpin 90°. Maka rasio ini tegangan untuk arus dalam rangkaian induktif akan menghasilkan persamaan yang mendefinisikan Reaktansi Induktif, XL dari kumparan/coil.
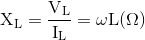
Kita dapat menulis ulang persamaan di atas untuk reaktansi induktif menjadi bentuk yang lebih akrab yang menggunakan frekuensi biasa dari supply daripada frekuensi sudut dalam radian, ω dan ini diberikan sebagai:
Dimana: ƒ adalah Frekuensi dan L adalah Induktansi dari Coil dan 2πƒ = ω.
Dari persamaan di atas untuk reaktansi induktif, dapat dilihat bahwa jika salah satu Frekuensi atau Induktansi ditingkatkan, nilai reaktansi induktif keseluruhan juga akan meningkat.
Ketika frekuensi mendekati tak terhingga reaktansi induktor juga akan meningkat menjadi tak terhingga yang bertindak seperti rangkaian terbuka.
Namun, ketika frekuensi mendekati nol atau DC, reaktansi induktor akan berkurang menjadi nol, bertindak seperti korsleting. Ini berarti bahwa reaktansi induktif “sebanding” terhadap frekuensi.
Dengan kata lain, reaktansi induktif meningkat dengan frekuensi yang menghasilkan XL menjadi kecil pada frekuensi rendah dan XL menjadi tinggi pada frekuensi tinggi dan ini ditunjukkan dalam grafik berikut:
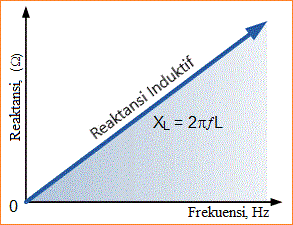
Kemiringan menunjukkan bahwa "Reaktansi Induktif" dari sebuah induktor meningkat dengan meningkatnya frekuensi supply. Oleh karena itu, Reaktansi Induktif sebanding dengan pemberian frekuensi: ( XL α ƒ )
Kemudian kita dapat melihat bahwa di DC sebuah induktor memiliki reaktansi nol (hubung singkat), pada frekuensi tinggi induktor memiliki reaktansi tak terbatas (rangkaian terbuka).

Dalam rangkaian AC yang berisi induktansi, L dan resistansi, R tegangan, V akan menjadi jumlah fasor dari dua tegangan komponen, VR dan VL. Ini berarti kemudian bahwa arus yang mengalir melalui coil masih akan tertinggal tegangan, tetapi dengan jumlah kurang dari 90° tergantung pada nilai-nilai VR dan VL.
Sudut fasa baru antara tegangan dan arus dikenal sebagai sudut fasa rangkaian dan diberi simbol Yunani phi, Φ.
Untuk dapat menghasilkan diagram vektor hubungan antara tegangan dan arus, referensi atau komponen umum harus ditemukan. Dalam rangkaian R-L yang terhubung seri, arus adalah umum karena arus yang sama mengalir melalui masing-masing komponen. Vektor kuantitas referensi ini umumnya digambar secara horizontal dari kiri ke kanan.
Dari tutorial kami tentang Rangkaian RC atau Resistor dan Capasitor , kami tahu bahwa arus dan tegangan dalam Rangkaian AC resistif sama-sama "dalam-fasa" dan karenanya vektor, VR digambar di atas skala pada jalur arus atau referensi.
Kita juga tahu dari atas, bahwa arus “tertinggal” tegangan di rangkaian induktif murni dan karena itu vektor, VL ditarik 90° di depan referensi arus dan dengan skala yang sama seperti VR dan ini ditunjukkan di bawah.
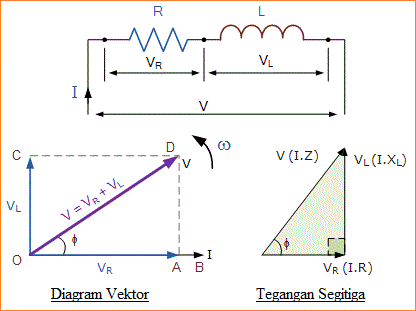
Dalam diagram vektor di atas dapat dilihat bahwa garis OB mewakili garis referensi arus, garis OA adalah tegangan dari komponen resistif dan yang berada dalam-fasa dengan arus.
Baris OC menunjukkan tegangan induktif yang 90° di depan arus, oleh karena itu dapat dilihat bahwa arus tertinggal tegangan sebesar 90°.
Jalur OD memberi kita tegangan resultan atau supply melintasi rangkaian. Segitiga tegangan berasal dari teorema Pythagoras dan diberikan sebagai:
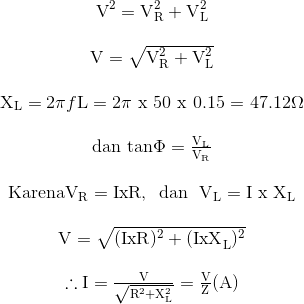
Dalam rangkaian DC, rasio tegangan terhadap arus disebut resistansi. Namun, dalam rangkaian AC rasio ini dikenal sebagai Impedansi, Z dengan unit lagi dalam Ohm. Impedansi adalah resistan total terhadap aliran arus dalam “rangkaian AC” yang mengandung resistansi dan reaktansi induktif.
Jika kita membagi sisi-sisi segitiga tegangan di atas oleh arus, segitiga lain diperoleh yang sisi-sisinya mewakili resistansi, reaktansi, dan impedansi coil/kumparan. Segitiga baru ini disebut "Segitiga Impedansi"

a) Tegangan supply jika frekuensinya 50Hz.

b) Sudut fasa antara tegangan dan arus.
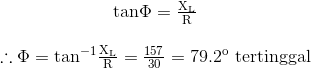
Dalam rangkaian AC induktif murni arus akan diluar-fasa dengan penuh 90° untuk tegangan supply. Dengan demikian, total daya reaktif yang dikonsumsi oleh coil akan sama dengan nol karena setiap daya yang dikonsumsi dibatalkan oleh daya ggl yang diinduksi sendiri yang dihasilkan.
Dengan kata lain, daya bersih dalam watt yang dikonsumsi oleh induktor murni pada akhir satu siklus lengkap adalah nol, karena energi diambil dari supply dan dikembalikan ke supply.
Daya Reaktif, ( Q ) dari coil dapat diberikan sebagai: I2 x XL (mirip dengan I2R dalam rangkaian DC). Kemudian tiga sisi segitiga daya dalam rangkaian AC diwakili oleh daya semu, ( S ), daya nyata, ( P ) dan daya reaktif, ( Q ) seperti yang ditunjukkan.

Perhatikan bahwa sebuah induktor aktual atau coil akan mengkonsumsi daya dalam watt karena resistansi dari gulungan menciptakan impedansi, Z.
Sejauh ini kita telah melihat perilaku Induktor yang terhubung ke supply DC dan mudah-mudahan sekarang kita tahu bahwa ketika tegangan DC diterapkan pada induktor, pertumbuhan arus melalui itu tidak instan tetapi ditentukan oleh induktor yang diinduksi sendiri atau nilai ggl-balik.
Kami juga melihat bahwa arus induktor terus naik hingga mencapai kondisi stabil maksimum setelah lima konstanta waktu. Arus maksimum mengalir melalui coil induktif hanya dibatasi oleh bagian resistif dari gulungan coil dalam Ohm, dan seperti yang kita tahu dari hukum Ohm, ini ditentukan oleh rasio tegangan terhadap arus, V/R.
Ketika tegangan AC atau bolak-balik diterapkan pada sebuah induktor, aliran arus yang melaluinya berperilaku sangat berbeda dengan tegangan DC yang diterapkan. Efek dari supply sinusoidal menghasilkan perbedaan fasa antara tegangan dan bentuk gelombang arus.
Sekarang di rangkaian AC, perlawanan terhadap aliran arus melalui gulungan coil tidak hanya tergantung pada induktansi coil tetapi juga frekuensi bentuk gelombang AC.
Perlawanan terhadap arus yang mengalir melalui coil di rangkaian AC ditentukan oleh resistansi AC, atau yang lebih dikenal sebagai Impedansi (Z), dari rangkaian.
Tetapi resistansi selalu dikaitkan dengan rangkaian DC sehingga untuk membedakan resistansi DC dari resistansi AC, istilah Reaktansi umumnya digunakan.
Sama seperti resistansi, nilai reaktansi juga diukur dalam Ohm tetapi diberi simbol X, (huruf besar "X"), untuk membedakannya dari nilai resistif murni.
Karena komponen yang kami bahas adalah induktor, maka reaktansi pada sebuah induktor disebut “Reaktansi Induktif”. Dengan kata lain, resistansi listrik induktor ketika digunakan dalam rangkaian AC disebut Reaktansi Induktif.
Reaktansi Induktif yang diberi simbol XL, adalah properti dalam rangkaian AC yang menentang perubahan arus. Dalam tutorial kami tentang Kapasitor dalam Rangkaian AC, kami melihat bahwa dalam rangkaian kapasitif murni, arus IC "MEMIMPIN" tegangan sebesar 90°. Dalam rangkaian AC murni induktif sebaliknya adalah benar, arus IL “TERTINGGAL” tegangan yang diberikan oleh 90°, atau (π/2 rad).
Induktor dalam Rangkaian AC

Dalam rangkaian induktif murni di atas, induktor terhubung langsung melintasi tegangan supply AC. Ketika tegangan supply meningkat dan menurun dengan frekuensi, ggl-balik yang diinduksi sendiri juga meningkat dan berkurang dalam coil sehubungan dengan perubahan ini.
Kita tahu bahwa ggl yang diinduksi sendiri ini berbanding lurus dengan laju perubahan arus melalui coil dan paling besar sebagai tegangan supply melintas dari setengah siklus positif ke setengah siklus negatif atau sebaliknya pada titik, 0° dan 180° sepanjang gelombang sinus.
Akibatnya, tingkat perubahan tegangan minimum terjadi ketika gelombang sinus AC melintasi pada level tegangan puncak maksimum atau minimum. Pada posisi ini dalam siklus, arus maksimum atau minimum mengalir melalui rangkaian induktor dan ini ditunjukkan di bawah ini.
Diagram Fasor Induktor AC

Tegangan dan arus gelombang ini menunjukkan bahwa untuk rangkaian induktif murni arus tertinggal tegangan sebesar 90°. Walaupun begitu, kita juga dapat mengatakan bahwa tegangan memimpin arus sebesar 90°.
Bagaimanapun juga ekspresi umum adalah bahwa arus tertinggal seperti yang ditunjukkan pada diagram vektor. Berikut vektor arus dan vektor tegangan ditampilkan displaced oleh 90°. Arus tertinggal dari tegangan.
Kami juga dapat menulis pernyataan ini sebagai, VL = 0° dan IL = -90° sehubungan dengan tegangan, VL. Jika bentuk gelombang tegangan digolongkan sebagai gelombang sinus maka arus, IL dapat digolongkan sebagai cosinus negatif dan kita dapat menentukan nilai arus pada titik waktu sebagai:
IL = Imax sin(ωt-90°)
Di mana: ω dalam radian per detik dan t dalam detik (second).
Sejak arus tertinggal tegangan sebesar 90° di rangkaian induktif murni, kita dapat menemukan fasa arus dengan mengetahui fasa tegangan atau sebaliknya. Jadi jika kita tahu nilai VL, maka IL harus tertinggal sebesar 90°.
Demikian juga, jika kita tahu nilai IL maka VL karena itu harus memimpin 90°. Maka rasio ini tegangan untuk arus dalam rangkaian induktif akan menghasilkan persamaan yang mendefinisikan Reaktansi Induktif, XL dari kumparan/coil.
Reaktansi Induktif
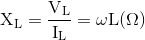
Kita dapat menulis ulang persamaan di atas untuk reaktansi induktif menjadi bentuk yang lebih akrab yang menggunakan frekuensi biasa dari supply daripada frekuensi sudut dalam radian, ω dan ini diberikan sebagai:
XL =2πƒL
Dimana: ƒ adalah Frekuensi dan L adalah Induktansi dari Coil dan 2πƒ = ω.
Dari persamaan di atas untuk reaktansi induktif, dapat dilihat bahwa jika salah satu Frekuensi atau Induktansi ditingkatkan, nilai reaktansi induktif keseluruhan juga akan meningkat.
Ketika frekuensi mendekati tak terhingga reaktansi induktor juga akan meningkat menjadi tak terhingga yang bertindak seperti rangkaian terbuka.
Namun, ketika frekuensi mendekati nol atau DC, reaktansi induktor akan berkurang menjadi nol, bertindak seperti korsleting. Ini berarti bahwa reaktansi induktif “sebanding” terhadap frekuensi.
Dengan kata lain, reaktansi induktif meningkat dengan frekuensi yang menghasilkan XL menjadi kecil pada frekuensi rendah dan XL menjadi tinggi pada frekuensi tinggi dan ini ditunjukkan dalam grafik berikut:
Reaksi Induktif Terhadap Frekuensi

Kemiringan menunjukkan bahwa "Reaktansi Induktif" dari sebuah induktor meningkat dengan meningkatnya frekuensi supply. Oleh karena itu, Reaktansi Induktif sebanding dengan pemberian frekuensi: ( XL α ƒ )
Kemudian kita dapat melihat bahwa di DC sebuah induktor memiliki reaktansi nol (hubung singkat), pada frekuensi tinggi induktor memiliki reaktansi tak terbatas (rangkaian terbuka).
Contoh Reaktansi Induktif No.1
Kumparan atau coil induktansi 150mH dan nol resistan terhubung di 100V, supply 50Hz. Hitung reaktansi induktif coil dan arus yang mengalir melewatinya.
Supply AC melalui Rangkaian R-L Seri
Sejauh ini kami telah mempertimbangkan coil induktif murni, tetapi tidak mungkin untuk memiliki induktansi murni karena semua kumparan/coil, relai atau solenoida akan memiliki sejumlah resistansi tidak peduli seberapa kecil yang terkait dengan kumparan belitan kawat yang digunakan. Kemudian kita dapat menganggap coil sederhana kita sebagai suatu resistansi seri dengan induktansi.Dalam rangkaian AC yang berisi induktansi, L dan resistansi, R tegangan, V akan menjadi jumlah fasor dari dua tegangan komponen, VR dan VL. Ini berarti kemudian bahwa arus yang mengalir melalui coil masih akan tertinggal tegangan, tetapi dengan jumlah kurang dari 90° tergantung pada nilai-nilai VR dan VL.
Sudut fasa baru antara tegangan dan arus dikenal sebagai sudut fasa rangkaian dan diberi simbol Yunani phi, Φ.
Untuk dapat menghasilkan diagram vektor hubungan antara tegangan dan arus, referensi atau komponen umum harus ditemukan. Dalam rangkaian R-L yang terhubung seri, arus adalah umum karena arus yang sama mengalir melalui masing-masing komponen. Vektor kuantitas referensi ini umumnya digambar secara horizontal dari kiri ke kanan.
Dari tutorial kami tentang Rangkaian RC atau Resistor dan Capasitor , kami tahu bahwa arus dan tegangan dalam Rangkaian AC resistif sama-sama "dalam-fasa" dan karenanya vektor, VR digambar di atas skala pada jalur arus atau referensi.
Kita juga tahu dari atas, bahwa arus “tertinggal” tegangan di rangkaian induktif murni dan karena itu vektor, VL ditarik 90° di depan referensi arus dan dengan skala yang sama seperti VR dan ini ditunjukkan di bawah.
Rangkaian AC Seri R-L

Dalam diagram vektor di atas dapat dilihat bahwa garis OB mewakili garis referensi arus, garis OA adalah tegangan dari komponen resistif dan yang berada dalam-fasa dengan arus.
Baris OC menunjukkan tegangan induktif yang 90° di depan arus, oleh karena itu dapat dilihat bahwa arus tertinggal tegangan sebesar 90°.
Jalur OD memberi kita tegangan resultan atau supply melintasi rangkaian. Segitiga tegangan berasal dari teorema Pythagoras dan diberikan sebagai:
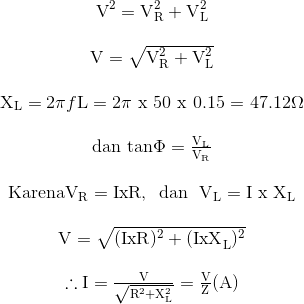
Dalam rangkaian DC, rasio tegangan terhadap arus disebut resistansi. Namun, dalam rangkaian AC rasio ini dikenal sebagai Impedansi, Z dengan unit lagi dalam Ohm. Impedansi adalah resistan total terhadap aliran arus dalam “rangkaian AC” yang mengandung resistansi dan reaktansi induktif.
Jika kita membagi sisi-sisi segitiga tegangan di atas oleh arus, segitiga lain diperoleh yang sisi-sisinya mewakili resistansi, reaktansi, dan impedansi coil/kumparan. Segitiga baru ini disebut "Segitiga Impedansi"
Segitiga Impedansi

Contoh Reaktansi Induktif No.2
Coil/kumparan solenoida memiliki resistansi 30 Ohm dan induktansi 0,5H. Jika arus yang mengalir melalui coil adalah 4 amp. Hitung,a) Tegangan supply jika frekuensinya 50Hz.

b) Sudut fasa antara tegangan dan arus.
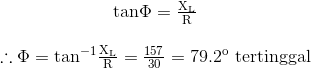
Segitiga Daya dari Induktor AC
Ada satu jenis konfigurasi segitiga yang bisa kita gunakan untuk rangkaian induktif dan itu adalah "Segitiga Daya". Daya dalam rangkaian induktif dikenal sebagai Daya Reaktif atau reaktif volt-amp, simbol Var yang diukur dalam volt-amp. Dalam rangkaian AC R-L Seri, arus meninggalkan tegangan supply dengan sudut Φ°.Dalam rangkaian AC induktif murni arus akan diluar-fasa dengan penuh 90° untuk tegangan supply. Dengan demikian, total daya reaktif yang dikonsumsi oleh coil akan sama dengan nol karena setiap daya yang dikonsumsi dibatalkan oleh daya ggl yang diinduksi sendiri yang dihasilkan.
Dengan kata lain, daya bersih dalam watt yang dikonsumsi oleh induktor murni pada akhir satu siklus lengkap adalah nol, karena energi diambil dari supply dan dikembalikan ke supply.
Daya Reaktif, ( Q ) dari coil dapat diberikan sebagai: I2 x XL (mirip dengan I2R dalam rangkaian DC). Kemudian tiga sisi segitiga daya dalam rangkaian AC diwakili oleh daya semu, ( S ), daya nyata, ( P ) dan daya reaktif, ( Q ) seperti yang ditunjukkan.
Segitiga Daya

Perhatikan bahwa sebuah induktor aktual atau coil akan mengkonsumsi daya dalam watt karena resistansi dari gulungan menciptakan impedansi, Z.