Kapasitansi pada Rangkaian AC
Kapasitor yang terhubung ke supply sinusoidal menghasilkan reaktansi dari efek frekuensi supply dan ukuran kapasitor. Ketika kapasitor dihubungkan melalui tegangan supply DC arus searah, kapasitor akan dibebankan ke nilai tegangan yang diberikan, bertindak seperti perangkat penyimpanan sementara dan mempertahankan atau menahan muatan ini tanpa batas selama tegangan supply ada.
Selama proses pengisian ini, arus pengisian, (i) akan mengalir ke kapasitor yang menentang setiap perubahan tegangan pada laju yang sama dengan laju perubahan muatan listrik pada plat. Arus pengisian ini dapat didefinisikan sebagai: i = CdV/dt. Setelah kapasitor "terisi penuh" kapasitor memblokir aliran elektron lagi ke plat-nya karena mereka menjadi jenuh.
Namun, jika kita menerapkan arus bolak-balik atau supply AC, kapasitor akan mengisi dan melepaskan secara bergantian pada frekuensi yang ditentukan oleh frekuensi supply. Kemudian Kapasitansi dalam Rangkaian AC bervariasi dengan frekuensi karena kapasitor terus diisi dan dikosongkan.
Kita tahu bahwa aliran elektron ke plat kapasitor berbanding lurus dengan laju perubahan tegangan di plat itu. Kemudian, kita dapat melihat bahwa kapasitor dalam rangkaian AC suka melewatkan arus ketika tegangan melintasi plat-nya terus berubah sehubungan dengan waktu seperti pada sinyal AC, tetapi tidak suka melewatkan arus ketika tegangan yang diberikan memiliki nilai konstan seperti pada sinyal DC. Pertimbangkan rangkaian di bawah ini.
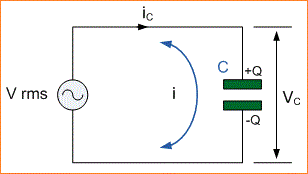
Dalam rangkaian kapasitif murni di atas, kapasitor terhubung langsung melintasi tegangan supply AC. Ketika tegangan supply meningkat dan menurun, kapasitor mengisi dan melepaskan sehubungan dengan perubahan ini.
Kita tahu bahwa arus pengisian berbanding lurus dengan laju perubahan tegangan di seluruh plat dengan laju perubahan ini paling besar karena tegangan supply melintas dari setengah siklus positif ke setengah siklus negatif atau sebaliknya di titik, 0° dan 180° sepanjang gelombang sinusoidal.
Akibatnya, perubahan tegangan paling kecil terjadi ketika gelombang sinus AC melintas pada level tegangan puncak maksimum atau minimum, ( Vm ). Pada posisi ini dalam siklus, arus maksimum atau minimum mengalir melalui rangkaian kapasitor dan ini ditunjukkan di bawah ini.
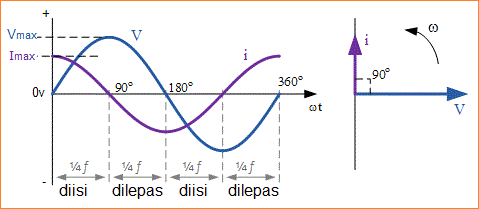
Pada 0° laju perubahan tegangan supply meningkat ke arah positif yang menghasilkan arus pengisian maksimum pada saat itu. Sebagai tegangan diterapkan mencapai nilai puncak maksimum pada 90° untuk saat yang sangat singkat dalam waktu tegangan supply yang tidak meningkat atau menurun sehingga tidak ada arus yang mengalir melalui rangkaian.
Sebagai tegangan diterapkan mulai menurun ke nol pada 180°, kemiringan tegangan negatif sehingga pembuangan kapasitor ke arah negatif. Pada titik 180° sepanjang garis laju perubahan tegangan berada pada maksimumnya lagi sehingga arus maksimum mengalir pada saat itu dan seterusnya.
Kemudian kita dapat mengatakan bahwa untuk kapasitor dalam rangkaian AC arus sesaat adalah pada minimum atau nol setiap kali tegangan yang diberikan adalah maksimum dan juga nilai sesaat dari arus adalah pada nilai maksimum atau puncaknya ketika tegangan yang diterapkan pada minimum atau nol.
Dari bentuk gelombang di atas, kita dapat melihat bahwa arus memimpin tegangan dengan 1/4 siklus atau 90° seperti yang ditunjukkan oleh diagram vektor. Maka kita dapat mengatakan bahwa dalam rangkaian murni kapasitif tegangan bolak tertinggal arus sebesar 90°.
Kita tahu bahwa arus yang mengalir melalui kapasitansi di rangkaian AC bertentangan dengan laju perubahan tegangan yang diberikan tetapi sama seperti resistor, kapasitor juga menawarkan beberapa bentuk perlawanan terhadap aliran arus melalui rangkaian, tetapi dengan kapasitor di AC rangkaian resistansi AC ini dikenal sebagai Reaktansi atau lebih umum di rangkaian kapasitor, Reaktansi Kapasitif, sehingga kapasitansi di rangkaian AC mengalami Reaktansi Kapasitif.
Karena reaktansi adalah jumlah yang juga dapat diterapkan pada Induktor serta Kapasitor, ketika digunakan dengan kapasitor, itu lebih dikenal sebagai Reaktansi Kapasitif.
Untuk kapasitor di rangkaian AC, reaktansi kapasitif diberikan simbol Xc. Maka kita dapat benar-benar mengatakan bahwa Reaktansi Kapasitif adalah nilai resistif kapasitor yang bervariasi dengan frekuensi. Juga, reaktansi kapasitif tergantung pada kapasitansi kapasitor dalam Farad serta frekuensi bentuk gelombang AC dan rumus yang digunakan untuk mendefinisikan reaktansi kapasitif diberikan sebagai:
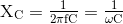
Di mana: F ada di Hertz dan C ada di Farad. 2πƒ juga dapat diekspresikan secara kolektif sebagai huruf Yunani Omega, ω untuk menunjukkan frekuensi sudut.
Dari rumus reaktansi kapasitif di atas, dapat dilihat bahwa jika salah satu dari Frekuensi atau Kapasitansi mana yang akan ditingkatkan, keseluruhan reaktansi kapasitif akan berkurang. Sebagai frekuensi mendekati tak terbatas reaktansi kapasitor akan berkurang menjadi nol bertindak seperti konduktor yang sempurna.
Namun, ketika frekuensi mendekati nol atau DC, reaktansi kapasitor akan meningkat hingga tak terbatas, bertindak seperti resistansi yang sangat besar. Ini berarti bahwa reaktansi kapasitif adalah " Berbanding terbalik " dengan frekuensi untuk setiap nilai Kapasitansi dan ini ditunjukkan di bawah ini:
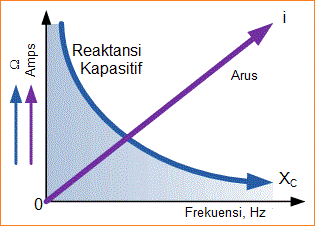
Reaktansi kapasitif kapasitor berkurang ketika frekuensi melewatinya sehingga reaktansi kapasitif berbanding terbalik dengan frekuensi. Perlawanan terhadap aliran arus, muatan elektrostatik pada plat (nilai kapasitansi AC-nya) tetap konstan karena menjadi lebih mudah bagi kapasitor untuk sepenuhnya menyerap perubahan muatan pada plat-nya selama setiap setengah siklus.
Juga ketika frekuensi meningkat, arus yang mengalir melalui kapasitor meningkat nilainya karena laju perubahan tegangan di plat-nya meningkat. Kemudian kita dapat melihat bahwa pada DC kapasitor memiliki reaktansi tak terbatas (rangkaian terbuka), pada frekuensi yang sangat tinggi kapasitor memiliki reaktansi nol (hubung singkat).
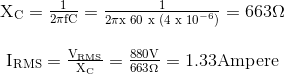
Di rangkaian AC, arus sinusoidal melalui kapasitor, yang mengarah tegangan sebesar 90°, bervariasi dengan frekuensi sebagai kapasitor sedang terus diisi dan dipakai oleh tegangan yang diberikan. Impedansi AC dari sebuah kapasitor dikenal sebagai Reaktansi dan karena kita berurusan dengan rangkaian kapasitor, lebih umum disebut Reaktansi Kapasitif, XC.
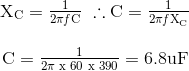
Reaktansi kapasitif ini berbanding terbalik dengan frekuensi dan menghasilkan perlawanan terhadap aliran arus di sekitar rangkaian kapasitif AC seperti yang kita lihat dalam tutorial Kapasitansi AC di bagian Teori AC.
Selama proses pengisian ini, arus pengisian, (i) akan mengalir ke kapasitor yang menentang setiap perubahan tegangan pada laju yang sama dengan laju perubahan muatan listrik pada plat. Arus pengisian ini dapat didefinisikan sebagai: i = CdV/dt. Setelah kapasitor "terisi penuh" kapasitor memblokir aliran elektron lagi ke plat-nya karena mereka menjadi jenuh.
Namun, jika kita menerapkan arus bolak-balik atau supply AC, kapasitor akan mengisi dan melepaskan secara bergantian pada frekuensi yang ditentukan oleh frekuensi supply. Kemudian Kapasitansi dalam Rangkaian AC bervariasi dengan frekuensi karena kapasitor terus diisi dan dikosongkan.
Kita tahu bahwa aliran elektron ke plat kapasitor berbanding lurus dengan laju perubahan tegangan di plat itu. Kemudian, kita dapat melihat bahwa kapasitor dalam rangkaian AC suka melewatkan arus ketika tegangan melintasi plat-nya terus berubah sehubungan dengan waktu seperti pada sinyal AC, tetapi tidak suka melewatkan arus ketika tegangan yang diberikan memiliki nilai konstan seperti pada sinyal DC. Pertimbangkan rangkaian di bawah ini.
Rangkaian Kapasitansi Kapasitor AC

Dalam rangkaian kapasitif murni di atas, kapasitor terhubung langsung melintasi tegangan supply AC. Ketika tegangan supply meningkat dan menurun, kapasitor mengisi dan melepaskan sehubungan dengan perubahan ini.
Kita tahu bahwa arus pengisian berbanding lurus dengan laju perubahan tegangan di seluruh plat dengan laju perubahan ini paling besar karena tegangan supply melintas dari setengah siklus positif ke setengah siklus negatif atau sebaliknya di titik, 0° dan 180° sepanjang gelombang sinusoidal.
Akibatnya, perubahan tegangan paling kecil terjadi ketika gelombang sinus AC melintas pada level tegangan puncak maksimum atau minimum, ( Vm ). Pada posisi ini dalam siklus, arus maksimum atau minimum mengalir melalui rangkaian kapasitor dan ini ditunjukkan di bawah ini.
Diagram Fasor Kapasitor AC

Pada 0° laju perubahan tegangan supply meningkat ke arah positif yang menghasilkan arus pengisian maksimum pada saat itu. Sebagai tegangan diterapkan mencapai nilai puncak maksimum pada 90° untuk saat yang sangat singkat dalam waktu tegangan supply yang tidak meningkat atau menurun sehingga tidak ada arus yang mengalir melalui rangkaian.
Sebagai tegangan diterapkan mulai menurun ke nol pada 180°, kemiringan tegangan negatif sehingga pembuangan kapasitor ke arah negatif. Pada titik 180° sepanjang garis laju perubahan tegangan berada pada maksimumnya lagi sehingga arus maksimum mengalir pada saat itu dan seterusnya.
Kemudian kita dapat mengatakan bahwa untuk kapasitor dalam rangkaian AC arus sesaat adalah pada minimum atau nol setiap kali tegangan yang diberikan adalah maksimum dan juga nilai sesaat dari arus adalah pada nilai maksimum atau puncaknya ketika tegangan yang diterapkan pada minimum atau nol.
Dari bentuk gelombang di atas, kita dapat melihat bahwa arus memimpin tegangan dengan 1/4 siklus atau 90° seperti yang ditunjukkan oleh diagram vektor. Maka kita dapat mengatakan bahwa dalam rangkaian murni kapasitif tegangan bolak tertinggal arus sebesar 90°.
Kita tahu bahwa arus yang mengalir melalui kapasitansi di rangkaian AC bertentangan dengan laju perubahan tegangan yang diberikan tetapi sama seperti resistor, kapasitor juga menawarkan beberapa bentuk perlawanan terhadap aliran arus melalui rangkaian, tetapi dengan kapasitor di AC rangkaian resistansi AC ini dikenal sebagai Reaktansi atau lebih umum di rangkaian kapasitor, Reaktansi Kapasitif, sehingga kapasitansi di rangkaian AC mengalami Reaktansi Kapasitif.
Reaktansi Kapasitif
Reaktansi Kapasitif dalam rangkaian kapasitif murni adalah perlawanan terhadap aliran arus di rangkaian AC saja. Seperti resistansi, reaktansi juga diukur dalam Ohm tetapi diberikan simbol X untuk membedakannya dari nilai resistif murni.Karena reaktansi adalah jumlah yang juga dapat diterapkan pada Induktor serta Kapasitor, ketika digunakan dengan kapasitor, itu lebih dikenal sebagai Reaktansi Kapasitif.
Untuk kapasitor di rangkaian AC, reaktansi kapasitif diberikan simbol Xc. Maka kita dapat benar-benar mengatakan bahwa Reaktansi Kapasitif adalah nilai resistif kapasitor yang bervariasi dengan frekuensi. Juga, reaktansi kapasitif tergantung pada kapasitansi kapasitor dalam Farad serta frekuensi bentuk gelombang AC dan rumus yang digunakan untuk mendefinisikan reaktansi kapasitif diberikan sebagai:
Rumus Reaktansi Kapasitif
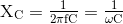
Di mana: F ada di Hertz dan C ada di Farad. 2πƒ juga dapat diekspresikan secara kolektif sebagai huruf Yunani Omega, ω untuk menunjukkan frekuensi sudut.
Dari rumus reaktansi kapasitif di atas, dapat dilihat bahwa jika salah satu dari Frekuensi atau Kapasitansi mana yang akan ditingkatkan, keseluruhan reaktansi kapasitif akan berkurang. Sebagai frekuensi mendekati tak terbatas reaktansi kapasitor akan berkurang menjadi nol bertindak seperti konduktor yang sempurna.
Namun, ketika frekuensi mendekati nol atau DC, reaktansi kapasitor akan meningkat hingga tak terbatas, bertindak seperti resistansi yang sangat besar. Ini berarti bahwa reaktansi kapasitif adalah " Berbanding terbalik " dengan frekuensi untuk setiap nilai Kapasitansi dan ini ditunjukkan di bawah ini:
Reaktansi Kapasitif terhadap Frekuensi

Reaktansi kapasitif kapasitor berkurang ketika frekuensi melewatinya sehingga reaktansi kapasitif berbanding terbalik dengan frekuensi. Perlawanan terhadap aliran arus, muatan elektrostatik pada plat (nilai kapasitansi AC-nya) tetap konstan karena menjadi lebih mudah bagi kapasitor untuk sepenuhnya menyerap perubahan muatan pada plat-nya selama setiap setengah siklus.
Juga ketika frekuensi meningkat, arus yang mengalir melalui kapasitor meningkat nilainya karena laju perubahan tegangan di plat-nya meningkat. Kemudian kita dapat melihat bahwa pada DC kapasitor memiliki reaktansi tak terbatas (rangkaian terbuka), pada frekuensi yang sangat tinggi kapasitor memiliki reaktansi nol (hubung singkat).
Contoh: Kapasitansi AC No.1
Temukan arus RMS yang mengalir dalam rangkaian kapasitif AC ketika kapasitor 4μF terhubung melalui supply 880V, 60Hz.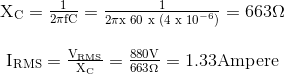
Di rangkaian AC, arus sinusoidal melalui kapasitor, yang mengarah tegangan sebesar 90°, bervariasi dengan frekuensi sebagai kapasitor sedang terus diisi dan dipakai oleh tegangan yang diberikan. Impedansi AC dari sebuah kapasitor dikenal sebagai Reaktansi dan karena kita berurusan dengan rangkaian kapasitor, lebih umum disebut Reaktansi Kapasitif, XC.
Contoh: Kapasitansi AC No.2
Ketika plat kapasitor paralel dihubungkan ke catu daya 60Hz, ternyata memiliki reaktansi 390 ohm. Hitung nilai kapasitor dalam micro-farad.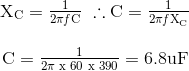
Reaktansi kapasitif ini berbanding terbalik dengan frekuensi dan menghasilkan perlawanan terhadap aliran arus di sekitar rangkaian kapasitif AC seperti yang kita lihat dalam tutorial Kapasitansi AC di bagian Teori AC.