Rangkaian Kapasitor Seri
Kapasitor dihubungkan bersama secara seri ketika mereka daisy chained bersama dalam satu baris. Untuk kapasitor yang terhubung seri, arus pengisian ( iC ) yang mengalir melalui kapasitor adalah SAMA untuk semua kapasitor karena hanya memiliki satu jalur untuk diikuti.
Kemudian, Kapasitor dalam Seri semua memiliki arus yang sama yang mengalir melalui mereka sebagai iT = i1 = i2 = i3 dll. Oleh karena itu setiap kapasitor akan menyimpan jumlah muatan listrik yang sama, Q pada platnya terlepas dari kapasitansinya.
Ini karena muatan yang disimpan oleh plat kapasitor mana saja pasti berasal dari plat kapasitor yang berdekatan. Oleh karena itu, kapasitor yang dihubungkan bersama secara seri harus memiliki muatan yang sama.
Pertimbangkan rangkaian berikut di mana tiga kapasitor, C1, C2 dan C3 semua terhubung bersama-sama dalam cabang seri di tegangan suplai antara titik A dan B.
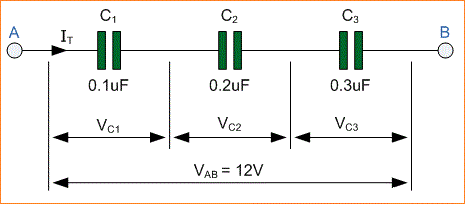
Pada rangkaian Kapasitor Paralel sebelumnya kita melihat bahwa kapasitansi total, CT dari rangkaian itu sama dengan jumlah dari semua kapasitor individu ditambahkan bersama-sama. Dalam serangkaian terhubung rangkaian Namun, total atau setara kapasitansi CT dihitung secara berbeda.
Dalam rangkaian seri di atas plat kanan kapasitor pertama, C1 terhubung ke plat kiri dari kapasitor kedua, C2 yang plat kanan dihubungkan ke plat kiri dari kapasitor ketiga, C3. Kemudian rangkaian seri ini berarti bahwa dalam rangkaian terhubung DC, kapasitor C2 secara efektif diisolasi dari rangkaian.
Hasil dari ini adalah bahwa area plat efektif telah menurun ke kapasitansi individu terkecil yang terhubung dalam rantai seri. Oleh karena itu penurunan tegangan pada masing-masing kapasitor akan berbeda tergantung pada nilai kapasitansi masing-masing.
Kemudian dengan menerapkan Hukum Kirchoff 2 - Tegangan ( KVL ) ke rangkaian di atas, kita mendapatkan:

Sejak Q = C*V dan menata ulang untuk V = Q/C, menggantikan Q/C untuk setiap tegangan kapasitor VC dalam persamaan KVL atas akan memberi kita:
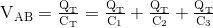
membagi setiap istilah melalui Q memberi
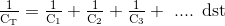
Ketika menambahkan Kapasitor bersama-sama dalam Seri, timbal balik ( 1/C ) dari masing-masing kapasitor ditambahkan bersama-sama (seperti Resistor Terhubung Paralel) dan bukan kapasitansi itu sendiri. Kemudian nilai total kapasitor dalam seri sama dengan kebalikan dari jumlah timbal balik dari masing-masing kapasitansi.
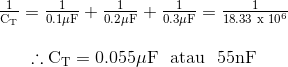
Satu hal penting untuk diingat tentang kapasitor yang terhubung bersama-sama dalam konfigurasi seri, adalah bahwa kapasitansi total rangkaian ( CT ) dari sejumlah kapasitor dihubungkan bersama dalam seri akan selalu KURANG dari nilai kapasitor terkecil dalam seri dan dalam contoh kami di atas CT = 0,055μF dengan nilai kapasitor terkecil dalam rantai seri hanya 0,1μF.
Metode perhitungan timbal balik ini dapat digunakan untuk menghitung sejumlah kapasitor individu yang terhubung bersama dalam jaringan seri tunggal. Namun, jika hanya ada dua kapasitor secara seri, maka rumus yang jauh lebih sederhana dan lebih cepat dapat digunakan dan diberikan sebagai:

Jika dua kapasitor seri dihubungkan adalah sama dan dari nilai yang sama, yaitu: C1 = C2, kita dapat menyederhanakan persamaan di atas lebih lanjut sebagai berikut untuk menemukan total kapasitansi dari kombinasi seri.
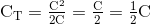
Maka kita dapat melihat bahwa jika dan hanya jika dua kapasitor terhubung seri adalah sama dan setara, maka total kapasitansi, CT akan persis sama dengan satu setengah dari nilai kapasitansi, yaitu: C/2.
Dengan Resistor yang terhubung seri, jumlah dari semua tegangan yang turun di rangkaian seri akan sama dengan tegangan yang diterapkan VS (Hukum Kirchoff 2 - Tegangan) dan ini juga berlaku untuk kapasitor dalam seri.
Dengan kapasitor terhubung seri, Reaktansi Kapasitif Kapasitor bertindak sebagai impedansi karena frekuensi supply. Reaktansi kapasitif ini menghasilkan penurunan tegangan pada masing-masing kapasitor, oleh karena itu kapasitor yang terhubung seri bertindak sebagai jaringan pembagi tegangan kapasitif.
Hasilnya adalah bahwa rumus Pembagi Tegangan yang diterapkan pada resistor juga dapat digunakan untuk menemukan tegangan individu untuk dua kapasitor secara seri. Kemudian:
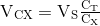
Di mana: CX adalah kapasitansi kapasitor yang dimaksud, VS adalah tegangan supply melintasi rantai seri dan VCX adalah penurunan tegangan melintasi kapasitor target.
a) masing-masing dua kapasitor dengan kapasitansi 47nF
b) satu kapasitor 470nF dihubungkan secara seri ke kapasitor 1μF
a) Total Kapasitansi Setara,

Tegangan jatuh di dua kapasitor 47nF identik,
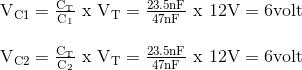
b) Total Kapasitansi Tidak Sama,
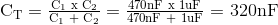
Tegangan turun di dua Kapasitor tidak identik: C1 = 470nF dan C2 = 1μF.
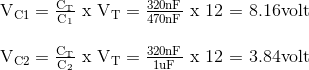
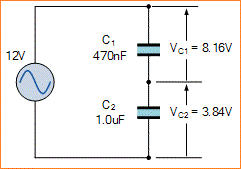
Karena hukum Kirchoff 2 - tegangan berlaku untuk ini dan setiap rangkaian seri terhubung, jumlah total penurunan tegangan individu akan sama nilainya dengan tegangan supply, VS. Kemudian 8,16 + 3,84 = 12V.
Perhatikan juga bahwa jika nilai kapasitor sama, 47nF dalam contoh pertama kami, tegangan supply akan dibagi rata di setiap kapasitor seperti yang ditunjukkan.
Hal Ini karena setiap kapasitor dalam rangkaian seri memiliki nilai yang sama dan jumlah tepat dari muatan ( Q = C x V = 0.564μC ) dan karena itu memiliki setengah (atau persentase fraksi selama lebih dari dua kapasitor) dari tegangan yang diberikan, VS.
Namun, ketika nilai kapasitor seri berbeda, kapasitor nilai yang lebih besar akan mengisi sendiri ke tegangan yang lebih rendah dan kapasitor nilai yang lebih kecil ke tegangan yang lebih tinggi, dan dalam contoh kedua kami di atas ini ditunjukkan masing-masing menjadi 3.84 dan 8.16 volt.
Perbedaan tegangan ini memungkinkan kapasitor mempertahankan jumlah muatan yang sama, Q pada plat masing-masing kapasitor seperti yang ditunjukkan.
Perhatikan bahwa rasio tegangan turun di dua kapasitor dihubungkan secara seri akan selalu tetap sama terlepas dari frekuensi supply sebagai reaktansi mereka, XC akan tetap proporsional sama. Kemudian dua tegangan turun 8.16 volt dan 3.84 volt di atas dalam contoh sederhana kami akan tetap sama bahkan jika frekuensi supply ditingkatkan dari 100Hz ke 100kHz.
Meskipun tegangan turun di masing-masing kapasitor akan berbeda untuk nilai kapasitansi yang berbeda, muatan coulomb melintasi plat akan sama karena jumlah arus yang sama ada di seluruh rangkaian seri karena semua kapasitor disupply dengan nomor yang sama atau jumlah yang sama dari elektron.
Dengan kata lain, jika muatan pada masing-masing plat kapasitor adalah sama, karena Q adalah konstan, maka ketika kapasitansinya menurun, penurunan tegangan pada plat kapasitor meningkat, karena muatannya besar sehubungan dengan kapasitansi. Demikian juga, kapasitansi yang lebih besar akan menghasilkan penurunan tegangan yang lebih kecil di plat-nya karena muatannya kecil sehubungan dengan kapasitansi.
Juga untuk kapasitor yang terhubung secara seri, semua kapasitor yang terhubung seri akan memiliki arus pengisian yang sama yang mengalir melalui mereka seperti iT = i1 = i2 = i3 dll. Dua atau lebih kapasitor dalam seri akan selalu memiliki jumlah muatan coulomb yang sama di seluruh plat mereka.
Seperti muatan, ( Q ) adalah sama dan konstan, penurunan tegangan kapasitor ditentukan oleh nilai dari kapasitor hanya sebagai V = Q ÷ C. Nilai kapasitansi yang kecil akan menghasilkan tegangan yang lebih besar sementara nilai kapasitansi yang besar akan menghasilkan penurunan tegangan yang lebih kecil.
Kemudian, Kapasitor dalam Seri semua memiliki arus yang sama yang mengalir melalui mereka sebagai iT = i1 = i2 = i3 dll. Oleh karena itu setiap kapasitor akan menyimpan jumlah muatan listrik yang sama, Q pada platnya terlepas dari kapasitansinya.
Ini karena muatan yang disimpan oleh plat kapasitor mana saja pasti berasal dari plat kapasitor yang berdekatan. Oleh karena itu, kapasitor yang dihubungkan bersama secara seri harus memiliki muatan yang sama.
QT = Q1 = Q2 = Q3 … .dst
Pertimbangkan rangkaian berikut di mana tiga kapasitor, C1, C2 dan C3 semua terhubung bersama-sama dalam cabang seri di tegangan suplai antara titik A dan B.
Rangkaian Kapasitor dalam Seri

Pada rangkaian Kapasitor Paralel sebelumnya kita melihat bahwa kapasitansi total, CT dari rangkaian itu sama dengan jumlah dari semua kapasitor individu ditambahkan bersama-sama. Dalam serangkaian terhubung rangkaian Namun, total atau setara kapasitansi CT dihitung secara berbeda.
Dalam rangkaian seri di atas plat kanan kapasitor pertama, C1 terhubung ke plat kiri dari kapasitor kedua, C2 yang plat kanan dihubungkan ke plat kiri dari kapasitor ketiga, C3. Kemudian rangkaian seri ini berarti bahwa dalam rangkaian terhubung DC, kapasitor C2 secara efektif diisolasi dari rangkaian.
Hasil dari ini adalah bahwa area plat efektif telah menurun ke kapasitansi individu terkecil yang terhubung dalam rantai seri. Oleh karena itu penurunan tegangan pada masing-masing kapasitor akan berbeda tergantung pada nilai kapasitansi masing-masing.
Kemudian dengan menerapkan Hukum Kirchoff 2 - Tegangan ( KVL ) ke rangkaian di atas, kita mendapatkan:

Sejak Q = C*V dan menata ulang untuk V = Q/C, menggantikan Q/C untuk setiap tegangan kapasitor VC dalam persamaan KVL atas akan memberi kita:
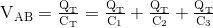
membagi setiap istilah melalui Q memberi
Persamaan Kapasitor Seri
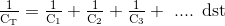
Ketika menambahkan Kapasitor bersama-sama dalam Seri, timbal balik ( 1/C ) dari masing-masing kapasitor ditambahkan bersama-sama (seperti Resistor Terhubung Paralel) dan bukan kapasitansi itu sendiri. Kemudian nilai total kapasitor dalam seri sama dengan kebalikan dari jumlah timbal balik dari masing-masing kapasitansi.
Contoh: Rangkaian Kapasitor Seri No.1
Mengambil tiga nilai kapasitor dari contoh di atas, kita dapat menghitung kapasitansi total, CT untuk tiga kapasitor secara seri seperti: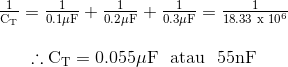
Satu hal penting untuk diingat tentang kapasitor yang terhubung bersama-sama dalam konfigurasi seri, adalah bahwa kapasitansi total rangkaian ( CT ) dari sejumlah kapasitor dihubungkan bersama dalam seri akan selalu KURANG dari nilai kapasitor terkecil dalam seri dan dalam contoh kami di atas CT = 0,055μF dengan nilai kapasitor terkecil dalam rantai seri hanya 0,1μF.
Metode perhitungan timbal balik ini dapat digunakan untuk menghitung sejumlah kapasitor individu yang terhubung bersama dalam jaringan seri tunggal. Namun, jika hanya ada dua kapasitor secara seri, maka rumus yang jauh lebih sederhana dan lebih cepat dapat digunakan dan diberikan sebagai:

Jika dua kapasitor seri dihubungkan adalah sama dan dari nilai yang sama, yaitu: C1 = C2, kita dapat menyederhanakan persamaan di atas lebih lanjut sebagai berikut untuk menemukan total kapasitansi dari kombinasi seri.
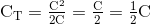
Maka kita dapat melihat bahwa jika dan hanya jika dua kapasitor terhubung seri adalah sama dan setara, maka total kapasitansi, CT akan persis sama dengan satu setengah dari nilai kapasitansi, yaitu: C/2.
Dengan Resistor yang terhubung seri, jumlah dari semua tegangan yang turun di rangkaian seri akan sama dengan tegangan yang diterapkan VS (Hukum Kirchoff 2 - Tegangan) dan ini juga berlaku untuk kapasitor dalam seri.
Dengan kapasitor terhubung seri, Reaktansi Kapasitif Kapasitor bertindak sebagai impedansi karena frekuensi supply. Reaktansi kapasitif ini menghasilkan penurunan tegangan pada masing-masing kapasitor, oleh karena itu kapasitor yang terhubung seri bertindak sebagai jaringan pembagi tegangan kapasitif.
Hasilnya adalah bahwa rumus Pembagi Tegangan yang diterapkan pada resistor juga dapat digunakan untuk menemukan tegangan individu untuk dua kapasitor secara seri. Kemudian:
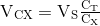
Di mana: CX adalah kapasitansi kapasitor yang dimaksud, VS adalah tegangan supply melintasi rantai seri dan VCX adalah penurunan tegangan melintasi kapasitor target.
Contoh: Rangkaian Kapasitor Seri No.2
Temukan kapasitansi keseluruhan dan tegangan RMS individu turun di set berikut dari dua kapasitor secara seri ketika terhubung ke catu daya AC 12V.a) masing-masing dua kapasitor dengan kapasitansi 47nF
b) satu kapasitor 470nF dihubungkan secara seri ke kapasitor 1μF
a) Total Kapasitansi Setara,

Tegangan jatuh di dua kapasitor 47nF identik,
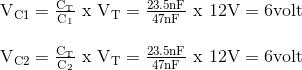
b) Total Kapasitansi Tidak Sama,
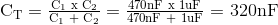
Tegangan turun di dua Kapasitor tidak identik: C1 = 470nF dan C2 = 1μF.
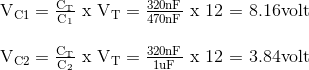

Perhatikan juga bahwa jika nilai kapasitor sama, 47nF dalam contoh pertama kami, tegangan supply akan dibagi rata di setiap kapasitor seperti yang ditunjukkan.
Hal Ini karena setiap kapasitor dalam rangkaian seri memiliki nilai yang sama dan jumlah tepat dari muatan ( Q = C x V = 0.564μC ) dan karena itu memiliki setengah (atau persentase fraksi selama lebih dari dua kapasitor) dari tegangan yang diberikan, VS.
Namun, ketika nilai kapasitor seri berbeda, kapasitor nilai yang lebih besar akan mengisi sendiri ke tegangan yang lebih rendah dan kapasitor nilai yang lebih kecil ke tegangan yang lebih tinggi, dan dalam contoh kedua kami di atas ini ditunjukkan masing-masing menjadi 3.84 dan 8.16 volt.
Perbedaan tegangan ini memungkinkan kapasitor mempertahankan jumlah muatan yang sama, Q pada plat masing-masing kapasitor seperti yang ditunjukkan.
QC1 = VC1 x C1 = 8.16V x 470nF = 3.84μC
QC2 = VC2 x C2 = 3.84V x 1uF = 3.84μC
Perhatikan bahwa rasio tegangan turun di dua kapasitor dihubungkan secara seri akan selalu tetap sama terlepas dari frekuensi supply sebagai reaktansi mereka, XC akan tetap proporsional sama. Kemudian dua tegangan turun 8.16 volt dan 3.84 volt di atas dalam contoh sederhana kami akan tetap sama bahkan jika frekuensi supply ditingkatkan dari 100Hz ke 100kHz.
Meskipun tegangan turun di masing-masing kapasitor akan berbeda untuk nilai kapasitansi yang berbeda, muatan coulomb melintasi plat akan sama karena jumlah arus yang sama ada di seluruh rangkaian seri karena semua kapasitor disupply dengan nomor yang sama atau jumlah yang sama dari elektron.
Dengan kata lain, jika muatan pada masing-masing plat kapasitor adalah sama, karena Q adalah konstan, maka ketika kapasitansinya menurun, penurunan tegangan pada plat kapasitor meningkat, karena muatannya besar sehubungan dengan kapasitansi. Demikian juga, kapasitansi yang lebih besar akan menghasilkan penurunan tegangan yang lebih kecil di plat-nya karena muatannya kecil sehubungan dengan kapasitansi.
Ringkasan Rangkaian Kapasitor Seri
Kemudian untuk meringkas, kapasitansi keseluruhan atau total, CT dari rangkaian yang mengandung Kapasitor di Seri adalah kebalikan dari jumlah timbal balik dari semua kapasitansi individu ditambahkan bersama-sama.Juga untuk kapasitor yang terhubung secara seri, semua kapasitor yang terhubung seri akan memiliki arus pengisian yang sama yang mengalir melalui mereka seperti iT = i1 = i2 = i3 dll. Dua atau lebih kapasitor dalam seri akan selalu memiliki jumlah muatan coulomb yang sama di seluruh plat mereka.
Seperti muatan, ( Q ) adalah sama dan konstan, penurunan tegangan kapasitor ditentukan oleh nilai dari kapasitor hanya sebagai V = Q ÷ C. Nilai kapasitansi yang kecil akan menghasilkan tegangan yang lebih besar sementara nilai kapasitansi yang besar akan menghasilkan penurunan tegangan yang lebih kecil.