Teorema Transfer Daya Maksimum beserta Contohnya
Teorema Transfer Daya Maksimum dapat didefinisikan sebagai, beban resistif terhubung ke jaringan DC, ketika resistansi beban (RL) adalah setara dengan resistansi internal kemudian menerima daya tertinggi yang dikenal sebagai resistansi setara teorema Thevenin dari jaringan sumber.
Teorema menentukan cara memilih resistansi beban (RL) ketika resistansi sumber diberikan satu kali. Ini adalah kesalahpahaman umum untuk menerapkan teorema dalam situasi terbalik. Itu tidak berarti bahwa bagaimana memilih resistansi sumber untuk spesifik resistansi beban (RL).
Sebenarnya, resistansi sumber yang membuat penggunaan terbaik transfer daya selalu nol, terlepas dari nilai resistansi beban. Teorema ini dapat diperluas ke rangkaian AC yang terdiri dari reaktansi dan menentukan bahwa transmisi daya tertinggi terjadi ketika impedansi beban (ZL) harus setara dengan ZTH (konjugat kompleks impedansi rangkaian yang sesuai).


Solusi:
Untuk menerapkan teorema transfer daya maksimum, kita perlu menemukan rangkaian setara Thevenin.
(a) Derivasi Vth dari rangkaian: tegangan rangkaian terbuka

Batasan: V1 = 100, V2 - 20 = Vx, dan V3 = Vth
Di simpul 2:

Di simpul 3:

(1)*2 + (2)*3 -> Vth = 120 [V]
(b) Derivasi Rth (dengan Metode Tegangan Uji): Setelah aplikasi penonaktifan & tegangan uji, kami memiliki:

Batasan: V3 = VT dan V2 = Vx
Di simpul 2:

Di simpul 3 (KCL):
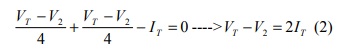
Dari (1) dan (2):
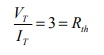
(c) Transfer Daya Maksimum: sekarang rangkaian dikurangi menjadi:

Untuk mendapatkan transfer daya maksimum, RL = 3 = Rth. Akhirnya, daya maksimum yang ditransfer ke RL adalah:

Tentukan daya maksimum yang dapat dikirim ke variabel resistor R.

Solusi:
(a) Vth: Tegangan rangkaian terbuka

Dari rangkaian, Vab = Vth = 40-10 = 30 [V]
(b) Rth: Mari kita menerapkan Metode Resistansi Input:
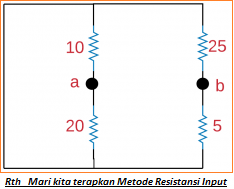
Kemudian Rab = (10//20) + (25//5) = 6.67 + 4.16 = 10.83 = Rth.
(c) Rangkaian Thevenin:


η = (Pmax/P) X 100 = 50%
Dimana; daya maksimum (Pmax)
Pmax = V2TH RTH/( RTH + RTH )2 = V2TH/4RTH
Dan daya yang disediakan (P) adalah
P = 2 V2TH/4RTH = V2TH/2RTH
η hanya 50% ketika transfer daya tertinggi tercapai, meskipun mencapai 100% ketika RL (resistansi beban) mencapai tak terbatas, sedangkan seluruh tahap daya cenderung nol.

Rangkaian di atas adalah rangkaian yang setara dengan Thevenin. Ketika rangkaian di atas dianggap melintasi terminal beban, maka aliran arus akan diberikan sebagai
I = VTH/ZTH + ZL
Di mana
ZL = RL + jXL
ZTH = RTH + jXTH
Karena itu,
I = VTH/(RL + jXL + RTH + jXTH)
= VTH/((RL + RTH) + j (XL + XTH))
Sirkulasi Daya ke beban,
PL = I2 RL
PL = V2TH × RL/((RL + RTH)2 + (XL + XTH)2) …… (1)
Untuk daya tertinggi, turunan persamaan di atas harus nol, setelah penyederhanaan kita bisa mendapatkan yang berikut.
XL + XTH = 0
XL = - XTH
Ganti nilai XL dalam persamaan di atas 1, dan kemudian kita bisa mendapatkan yang berikut.
PL = V2TH × RL/((RL + RTH) 2
Sekali lagi untuk transfer daya tertinggi, derivasi persamaan di atas harus sama dengan nol, setelah menyelesaikan ini kita bisa dapatkan
RL + RTH = 2 RL
RL = RTH
Oleh karena itu, daya tertinggi akan ditransmisikan dari sumber ke beban, jika RL (resistor beban) = RTH & XL = - XTH dalam rangkaian AC. Ini berarti bahwa impedansi beban (ZL) harus setara dengan ZTH (konjugat kompleks impedansi rangkaian yang sesuai)
ZL = ZTH
Daya maksimum yang ditransmisikan (Pmax) = V2TH/4 RL atau V2TH/4 RTH

PL = i2 RL = (V th/RTH + RL)2 x RL = V2TH RL/(RTH + RL )2
Karena VTH dan RTH ditetapkan untuk rangkaian tertentu, daya beban adalah fungsi dari resistansi beban RL.
Dengan membedakan PL sehubungan dengan RL dan mengatur hasilnya sama dengan nol, kami memiliki teorema transfer daya maksimum berikut; Daya maksimum terjadi ketika RL sama dengan RTH.
Ketika kondisi transfer daya maksimum terpenuhi, yaitu, RL = RTH, daya maksimum yang ditransfer adalah:
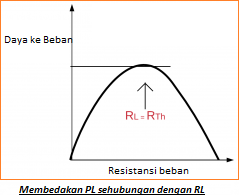
PL = V2TH RL/[RTH + RL ]2 = V2TH RTH/[RTH + RL ]2 = V2TH/4 RTH
Langkah 1: Lepaskan resistansi beban dari rangkaian.
Langkah 2: Temukan resistansi Thevenin (RTH) dari jaringan sumber yang melihat melalui terminal beban rangkaian terbuka.
Langkah 3: Sesuai dengan teorema transfer daya maksimum, RTH adalah resistansi beban jaringan, yaitu RL = RTH yang memungkinkan transfer daya maksimum.
Langkah 4: Transfer Daya Maksimum dihitung dengan persamaan di bawah ini
(Pmax) = V2TH/4 RTH

Solusi:
Menurut teorema ini, ketika daya tertinggi melalui beban, maka resistansi mirip dengan resistansi yang sama antara kedua ujung RL setelah dihilangkan.
Jadi, untuk penemuan resistansi beban (RL), kita harus menemukan resistansi yang setara:


jadi,

Sekarang, untuk menemukan daya tertinggi melalui resistansi beban-RL, kita harus menemukan nilai tegangan antara rangkaian VOC.
Untuk rangkaian di atas, terapkan analisis mesh. Kita bisa mendapatkan:
Terapkan KVL untuk loop-1:
6-6I1-8I1 + 8I2 = 0
-14I1 + 8I2 = -6 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (1)
Terapkan KVL untuk loop-2:
-8I2-5I2-12I2 + 8I1 = 0
8I1-25I2 = 0 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (2)
Dengan memecahkan dua persamaan di atas, kita dapatkan
I1 = 0.524 A
I2 = 0.167 A
Sekarang, dari rangkaian Voc
VA-5I2- VB = 0
Vo.c/VAB = 5I2 = 5X0.167 = 0.835v
Karenanya, daya maksimum melalui resistansi beban (RL) adalah;
P maks = VOC2/4RL = (0.835 x 0.835)/4 x 3.77 = 0.046 watt
Temukan daya tertinggi yang dapat ditransmisikan ke resistor beban-RL dari rangkaian di bawah ini.

Solusi:
Terapkan teorema Thevenin ke rangkaian di atas,
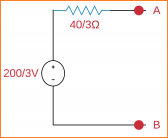
Di sini, tegangan Thevenin (Vth) = (200/3) dan resistansi Thevenin (Rth) = (40/3) Ω
Ganti fraksi rangkaian, yaitu sisi kiri terminal A & B dari rangkaian yang diberikan dengan rangkaian setara Thevenin. Diagram rangkaian sekunder ditunjukkan di bawah ini.

Kita dapat menemukan daya maksimum yang akan dikirim ke resistor beban, RL dengan menggunakan rumus berikut.
PL, Max = V2TH/4 RTH
Pengganti VTh = (200/3) V dan RTh = (40/3) Ω dalam rumus di atas.
PL, Max = (200/3)2 /4 (40/3) = 250/3 watt
Oleh karena itu, daya maksimum yang akan dikirim ke resistor beban RL dari rangkaian yang diberikan adalah 250/3 W.
Teorema menentukan cara memilih resistansi beban (RL) ketika resistansi sumber diberikan satu kali. Ini adalah kesalahpahaman umum untuk menerapkan teorema dalam situasi terbalik. Itu tidak berarti bahwa bagaimana memilih resistansi sumber untuk spesifik resistansi beban (RL).
Sebenarnya, resistansi sumber yang membuat penggunaan terbaik transfer daya selalu nol, terlepas dari nilai resistansi beban. Teorema ini dapat diperluas ke rangkaian AC yang terdiri dari reaktansi dan menentukan bahwa transmisi daya tertinggi terjadi ketika impedansi beban (ZL) harus setara dengan ZTH (konjugat kompleks impedansi rangkaian yang sesuai).

Memecahkan Masalah Teorema Transfer Daya Maksimum
1. Temukan resistansi beban RL yang memungkinkan rangkaian (kiri terminal a dan b) untuk memberikan daya maksimum terhadap beban. Juga, temukan daya maksimum yang dikirim ke beban.
Solusi:
Untuk menerapkan teorema transfer daya maksimum, kita perlu menemukan rangkaian setara Thevenin.
(a) Derivasi Vth dari rangkaian: tegangan rangkaian terbuka

Batasan: V1 = 100, V2 - 20 = Vx, dan V3 = Vth
Di simpul 2:

Di simpul 3:

(1)*2 + (2)*3 -> Vth = 120 [V]
(b) Derivasi Rth (dengan Metode Tegangan Uji): Setelah aplikasi penonaktifan & tegangan uji, kami memiliki:

Batasan: V3 = VT dan V2 = Vx
Di simpul 2:

Di simpul 3 (KCL):
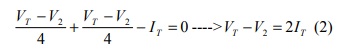
Dari (1) dan (2):
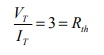
(c) Transfer Daya Maksimum: sekarang rangkaian dikurangi menjadi:

Untuk mendapatkan transfer daya maksimum, RL = 3 = Rth. Akhirnya, daya maksimum yang ditransfer ke RL adalah:

Tentukan daya maksimum yang dapat dikirim ke variabel resistor R.

Solusi:
(a) Vth: Tegangan rangkaian terbuka

Dari rangkaian, Vab = Vth = 40-10 = 30 [V]
(b) Rth: Mari kita menerapkan Metode Resistansi Input:

Kemudian Rab = (10//20) + (25//5) = 6.67 + 4.16 = 10.83 = Rth.
(c) Rangkaian Thevenin:


Rumus/Formula Teorema Transfer Daya Maksimum
Jika kita menganggap η (efisiensi) sebagai fraksi daya yang dilarutkan melalui beban R ke daya yang diperluas dengan sumber, VTH, maka mudah untuk menghitung efisiensi sebagaiη = (Pmax/P) X 100 = 50%
Dimana; daya maksimum (Pmax)
Pmax = V2TH RTH/( RTH + RTH )2 = V2TH/4RTH
Dan daya yang disediakan (P) adalah
P = 2 V2TH/4RTH = V2TH/2RTH
η hanya 50% ketika transfer daya tertinggi tercapai, meskipun mencapai 100% ketika RL (resistansi beban) mencapai tak terbatas, sedangkan seluruh tahap daya cenderung nol.
Teorema Transfer Daya Maksimum untuk Rangkaian AC
Seperti dalam pengaturan aktif, daya tertinggi ditransmisikan ke beban sementara impedansi beban setara dengan konjugat kompleks dari impedansi yang sesuai dari pengaturan yang diberikan seperti yang diamati dari terminal beban.
Rangkaian di atas adalah rangkaian yang setara dengan Thevenin. Ketika rangkaian di atas dianggap melintasi terminal beban, maka aliran arus akan diberikan sebagai
I = VTH/ZTH + ZL
Di mana
ZL = RL + jXL
ZTH = RTH + jXTH
Karena itu,
I = VTH/(RL + jXL + RTH + jXTH)
= VTH/((RL + RTH) + j (XL + XTH))
Sirkulasi Daya ke beban,
PL = I2 RL
PL = V2TH × RL/((RL + RTH)2 + (XL + XTH)2) …… (1)
Untuk daya tertinggi, turunan persamaan di atas harus nol, setelah penyederhanaan kita bisa mendapatkan yang berikut.
XL + XTH = 0
XL = - XTH
Ganti nilai XL dalam persamaan di atas 1, dan kemudian kita bisa mendapatkan yang berikut.
PL = V2TH × RL/((RL + RTH) 2
Sekali lagi untuk transfer daya tertinggi, derivasi persamaan di atas harus sama dengan nol, setelah menyelesaikan ini kita bisa dapatkan
RL + RTH = 2 RL
RL = RTH
Oleh karena itu, daya tertinggi akan ditransmisikan dari sumber ke beban, jika RL (resistor beban) = RTH & XL = - XTH dalam rangkaian AC. Ini berarti bahwa impedansi beban (ZL) harus setara dengan ZTH (konjugat kompleks impedansi rangkaian yang sesuai)
ZL = ZTH
Daya maksimum yang ditransmisikan (Pmax) = V2TH/4 RL atau V2TH/4 RTH
Contoh Teorema Transfer Daya Maksimum
Dalam beberapa aplikasi, tujuan rangkaian adalah untuk memberikan daya maksimum pada suatu beban. Beberapa contoh:- Amplifier stereo
- Pemancar radio
- Peralatan komunikasi

PL = i2 RL = (V th/RTH + RL)2 x RL = V2TH RL/(RTH + RL )2
Karena VTH dan RTH ditetapkan untuk rangkaian tertentu, daya beban adalah fungsi dari resistansi beban RL.
Dengan membedakan PL sehubungan dengan RL dan mengatur hasilnya sama dengan nol, kami memiliki teorema transfer daya maksimum berikut; Daya maksimum terjadi ketika RL sama dengan RTH.
Ketika kondisi transfer daya maksimum terpenuhi, yaitu, RL = RTH, daya maksimum yang ditransfer adalah:

PL = V2TH RL/[RTH + RL ]2 = V2TH RTH/[RTH + RL ]2 = V2TH/4 RTH
Langkah-langkah Untuk Memecahkan Teorema Transfer Daya Maksimum
Langkah-langkah di bawah ini digunakan untuk menyelesaikan masalah dengan Teorema Transfer Daya MaksimumLangkah 1: Lepaskan resistansi beban dari rangkaian.
Langkah 2: Temukan resistansi Thevenin (RTH) dari jaringan sumber yang melihat melalui terminal beban rangkaian terbuka.
Langkah 3: Sesuai dengan teorema transfer daya maksimum, RTH adalah resistansi beban jaringan, yaitu RL = RTH yang memungkinkan transfer daya maksimum.
Langkah 4: Transfer Daya Maksimum dihitung dengan persamaan di bawah ini
(Pmax) = V2TH/4 RTH
Contoh Masalah dengan Solusi Teorema Transfer Daya Maksimum
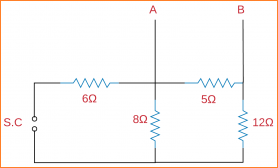
Temukan nilai RL untuk rangkaian di bawah ini bahwa daya tertinggi juga, temukan daya tertinggi melalui RL menggunakan teorema transfer daya maksimum.
Solusi:
Menurut teorema ini, ketika daya tertinggi melalui beban, maka resistansi mirip dengan resistansi yang sama antara kedua ujung RL setelah dihilangkan.
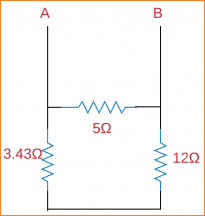
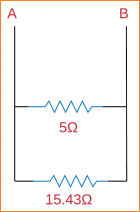
Jadi, untuk penemuan resistansi beban (RL), kita harus menemukan resistansi yang setara:





jadi,

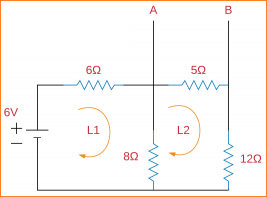
Sekarang, untuk menemukan daya tertinggi melalui resistansi beban-RL, kita harus menemukan nilai tegangan antara rangkaian VOC.

Untuk rangkaian di atas, terapkan analisis mesh. Kita bisa mendapatkan:
Terapkan KVL untuk loop-1:
6-6I1-8I1 + 8I2 = 0
-14I1 + 8I2 = -6 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (1)
Terapkan KVL untuk loop-2:
-8I2-5I2-12I2 + 8I1 = 0
8I1-25I2 = 0 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (2)
Dengan memecahkan dua persamaan di atas, kita dapatkan
I1 = 0.524 A
I2 = 0.167 A
Sekarang, dari rangkaian Voc
VA-5I2- VB = 0
Vo.c/VAB = 5I2 = 5X0.167 = 0.835v
Karenanya, daya maksimum melalui resistansi beban (RL) adalah;
P maks = VOC2/4RL = (0.835 x 0.835)/4 x 3.77 = 0.046 watt
Temukan daya tertinggi yang dapat ditransmisikan ke resistor beban-RL dari rangkaian di bawah ini.

Solusi:
Terapkan teorema Thevenin ke rangkaian di atas,

Di sini, tegangan Thevenin (Vth) = (200/3) dan resistansi Thevenin (Rth) = (40/3) Ω
Ganti fraksi rangkaian, yaitu sisi kiri terminal A & B dari rangkaian yang diberikan dengan rangkaian setara Thevenin. Diagram rangkaian sekunder ditunjukkan di bawah ini.

Kita dapat menemukan daya maksimum yang akan dikirim ke resistor beban, RL dengan menggunakan rumus berikut.
PL, Max = V2TH/4 RTH
Pengganti VTh = (200/3) V dan RTh = (40/3) Ω dalam rumus di atas.
PL, Max = (200/3)2 /4 (40/3) = 250/3 watt
Oleh karena itu, daya maksimum yang akan dikirim ke resistor beban RL dari rangkaian yang diberikan adalah 250/3 W.
Aplikasi Teorema Transfer Daya Maksimum
Teorema transfer daya maksimum dapat diterapkan dalam banyak cara untuk menentukan nilai resistansi beban yang menerima daya maksimum dari catu daya dan daya maksimum dalam kondisi transfer daya tertinggi. Di bawah ini adalah beberapa aplikasi dari teorema transfer daya maksimum:- Teorema ini selalu dicari dalam sistem komunikasi. Misalnya, dalam sistem alamat komunitas, rangkaian disesuaikan untuk transfer daya tertinggi dengan membuat speaker (resistansi beban) setara dengan amplifier (resistansi sumber). Ketika beban dan sumber telah cocok maka memiliki resistansi yang sama.
- Pada mesin mobil, daya yang ditransmisikan ke motor starter mobil akan tergantung pada daya tahan efektif motor & daya tahan baterai. Ketika kedua resistansi itu setara, maka daya tertinggi akan ditransmisikan ke motor untuk mengaktifkan mesin.