Analisis Arus Mesh
Analisis Arus Mesh adalah teknik yang digunakan untuk menemukan arus yang bersirkulasi di sekitar loop atau Mesh dengan jalur tertutup apa pun dari rangkaian.
Sementara Hukum Kirchoff memberi kita metode dasar untuk menganalisis setiap rangkaian listrik yang kompleks, ada berbagai cara untuk meningkatkan metode ini dengan menggunakan Analisis Arus Mesh atau Analisis Tegangan Nodal yang menghasilkan pengurangan matematika yang terlibat dan ketika jaringan besar terlibat pengurangan dalam matematika ini bisa menjadi keuntungan besar. Sebagai contoh, perhatikan contoh rangkaian listrik dari bagian sebelumnya.
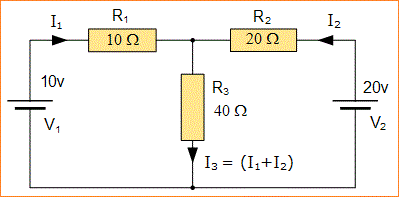
Salah satu metode sederhana untuk mengurangi penggunaan matematika yang terlibat adalah menganalisis rangkaian menggunakan persamaan Hukum Kirchoff 1 - Arus untuk menentukan arus, I1 dan I2 mengalir di dua resistor. Maka tidak perlu menghitung arus I3 karena hanya jumlah I1 dan I2. Jadi Hukum Kirchoff 2 -Tegangan menjadi:
Persamaan No 1: 10 = 50I1 + 40I2
Persamaan No 2: 20 = 40I1 + 60I2
Oleh karena itu, satu baris perhitungan matematika telah disimpan.
Sebagai aturan umum, hanya label loop dalam arah searah jarum jam dengan arus yang beredar karena tujuannya adalah untuk mencakup semua elemen rangkaian setidaknya satu kali. Setiap arus cabang yang diperlukan dapat ditemukan dari loop yang sesuai atau arus mesh seperti sebelumnya menggunakan metode Kirchoff.
Sebagai contoh: i1 = I1, i2 = -I2 dan I3 = I1 - I2
Kami sekarang menulis persamaan Hukum Kirchoff 2 - Tegangan dengan cara yang sama seperti sebelumnya untuk menyelesaikannya tetapi kelebihan dari metode ini adalah memastikan bahwa informasi yang diperoleh dari persamaan rangkaian adalah minimum yang diperlukan untuk menyelesaikan rangkaian karena informasinya lebih umum dan dapat mudah dimasukkan ke dalam bentuk matriks.
Sebagai contoh, perhatikan rangkaian dari bagian sebelumnya.
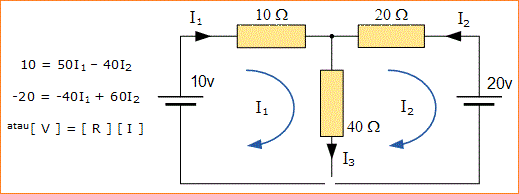
Persamaan ini dapat diselesaikan dengan cepat dengan menggunakan single Mesh impedansi matriks Z. Setiap elemen ON diagonal utama akan “positif” dan merupakan total impedansi dari setiap mesh. Dimana, setiap elemen OFF diagonal utama akan "nol" atau "negatif" dan mewakili elemen rangkaian yang menghubungkan semua mesh yang sesuai.
Pertama kita perlu memahami bahwa ketika berhadapan dengan matriks, untuk pembagian dua matriks itu sama dengan mengalikan satu matriks dengan kebalikan dari yang lain seperti yang ditunjukkan.

Setelah menemukan kebalikan dari R, karena V/R sama dengan V x R-1, kita sekarang dapat menggunakannya untuk menemukan dua arus yang bersirkulasi.

Dimana:
[V] memberikan tegangan baterai total untuk loop 1 dan kemudian loop 2
[I] menyatakan nama-nama arus loop yang sedang kami coba temukan
[R] adalah matriks resistansi
[R-1] adalah kebalikan dari matriks [R]
dan ini memberi I1 sebagai -0.143 Amp dan I2 sebagai -0.429 Amp
Karena: I3 = I1 - I2
Gabungan arus I3 karena itu diberikan sebagai: -0.143 - (-0.429) = 0.286 Amp, yang merupakan nilai yang sama dengan 0.286 amp, kami menemukan menggunakan Hukum Kirchoff Rangkaian di tutorial sebelumnya.
1. Beri label semua loop internal dengan arus yang bersirkulasi. ( I1, I2, ... IL dll)
2. Tulis matriks kolom [ L x 1 ] [ V ] yang memberikan jumlah semua sumber tegangan di setiap loop.
3. Tuliskan matriks [ L x L ], [ R ] untuk semua resistansi dalam rangkaian sebagai berikut:
R11 = resistansi total dalam loop pertama.
Rnn = resistansi total dalam loop ke-N.
RJK = resistansi yang langsung bergabung dengan loop J ke Loop K.
4. Tulis persamaan matriks atau vektor [V] = [R] x [I] di mana [I] adalah daftar arus yang dapat ditemukan.
Selain menggunakan Analisis Arus Mesh, kita juga dapat menggunakan analisis simpul untuk menghitung tegangan di sekitar loop, sekali lagi mengurangi penggunaan matematika yang diperlukan hanya dengan menggunakan Hukum Kirchoff.
Dalam tutorial berikutnya yang berkaitan dengan teori Rangkaian DC, kita akan melihat Analisis Tegangan Nodal untuk melakukan hal itu.
Sementara Hukum Kirchoff memberi kita metode dasar untuk menganalisis setiap rangkaian listrik yang kompleks, ada berbagai cara untuk meningkatkan metode ini dengan menggunakan Analisis Arus Mesh atau Analisis Tegangan Nodal yang menghasilkan pengurangan matematika yang terlibat dan ketika jaringan besar terlibat pengurangan dalam matematika ini bisa menjadi keuntungan besar. Sebagai contoh, perhatikan contoh rangkaian listrik dari bagian sebelumnya.
Rangkaian Analisis Arus Mesh

Salah satu metode sederhana untuk mengurangi penggunaan matematika yang terlibat adalah menganalisis rangkaian menggunakan persamaan Hukum Kirchoff 1 - Arus untuk menentukan arus, I1 dan I2 mengalir di dua resistor. Maka tidak perlu menghitung arus I3 karena hanya jumlah I1 dan I2. Jadi Hukum Kirchoff 2 -Tegangan menjadi:
Persamaan No 1: 10 = 50I1 + 40I2
Persamaan No 2: 20 = 40I1 + 60I2
Oleh karena itu, satu baris perhitungan matematika telah disimpan.
Analisis Arus Mesh
Metode yang lebih mudah untuk menyelesaikan rangkaian di atas adalah dengan menggunakan Analisis Arus Mesh atau Analisis Loop yang juga kadang-kadang disebut metode Sirkuilasi Arus Maxwell. Alih-alih memberi label arus cabang, kita perlu memberi label pada setiap "loop tertutup" dengan arus yang bersirkulasi.Sebagai aturan umum, hanya label loop dalam arah searah jarum jam dengan arus yang beredar karena tujuannya adalah untuk mencakup semua elemen rangkaian setidaknya satu kali. Setiap arus cabang yang diperlukan dapat ditemukan dari loop yang sesuai atau arus mesh seperti sebelumnya menggunakan metode Kirchoff.
Sebagai contoh: i1 = I1, i2 = -I2 dan I3 = I1 - I2
Kami sekarang menulis persamaan Hukum Kirchoff 2 - Tegangan dengan cara yang sama seperti sebelumnya untuk menyelesaikannya tetapi kelebihan dari metode ini adalah memastikan bahwa informasi yang diperoleh dari persamaan rangkaian adalah minimum yang diperlukan untuk menyelesaikan rangkaian karena informasinya lebih umum dan dapat mudah dimasukkan ke dalam bentuk matriks.
Sebagai contoh, perhatikan rangkaian dari bagian sebelumnya.

Persamaan ini dapat diselesaikan dengan cepat dengan menggunakan single Mesh impedansi matriks Z. Setiap elemen ON diagonal utama akan “positif” dan merupakan total impedansi dari setiap mesh. Dimana, setiap elemen OFF diagonal utama akan "nol" atau "negatif" dan mewakili elemen rangkaian yang menghubungkan semua mesh yang sesuai.
Pertama kita perlu memahami bahwa ketika berhadapan dengan matriks, untuk pembagian dua matriks itu sama dengan mengalikan satu matriks dengan kebalikan dari yang lain seperti yang ditunjukkan.

Setelah menemukan kebalikan dari R, karena V/R sama dengan V x R-1, kita sekarang dapat menggunakannya untuk menemukan dua arus yang bersirkulasi.

Dimana:
[V] memberikan tegangan baterai total untuk loop 1 dan kemudian loop 2
[I] menyatakan nama-nama arus loop yang sedang kami coba temukan
[R] adalah matriks resistansi
[R-1] adalah kebalikan dari matriks [R]
dan ini memberi I1 sebagai -0.143 Amp dan I2 sebagai -0.429 Amp
Karena: I3 = I1 - I2
Gabungan arus I3 karena itu diberikan sebagai: -0.143 - (-0.429) = 0.286 Amp, yang merupakan nilai yang sama dengan 0.286 amp, kami menemukan menggunakan Hukum Kirchoff Rangkaian di tutorial sebelumnya.
Ringkasan Analisis Arus Mesh
Ini "terlihat" metode analisis rangkaian mungkin yang terbaik dari semua metode analisis rangkaian dengan prosedur dasar untuk menyelesaikan persamaan Analisis Arus Mesh adalah sebagai berikut:1. Beri label semua loop internal dengan arus yang bersirkulasi. ( I1, I2, ... IL dll)
2. Tulis matriks kolom [ L x 1 ] [ V ] yang memberikan jumlah semua sumber tegangan di setiap loop.
3. Tuliskan matriks [ L x L ], [ R ] untuk semua resistansi dalam rangkaian sebagai berikut:
R11 = resistansi total dalam loop pertama.
Rnn = resistansi total dalam loop ke-N.
RJK = resistansi yang langsung bergabung dengan loop J ke Loop K.
4. Tulis persamaan matriks atau vektor [V] = [R] x [I] di mana [I] adalah daftar arus yang dapat ditemukan.
Selain menggunakan Analisis Arus Mesh, kita juga dapat menggunakan analisis simpul untuk menghitung tegangan di sekitar loop, sekali lagi mengurangi penggunaan matematika yang diperlukan hanya dengan menggunakan Hukum Kirchoff.
Dalam tutorial berikutnya yang berkaitan dengan teori Rangkaian DC, kita akan melihat Analisis Tegangan Nodal untuk melakukan hal itu.