Aturan dan Hukum Aljabar Boolean

Aljabar Boolean menggunakan seperangkat Hukum dan Aturan untuk menentukan operasi rangkain logika digital.

Selain simbol logika "0" dan "1" yang digunakan untuk merepresentasikan input atau output digital, kita juga dapat menggunakannya sebagai konstanta untuk rangkaian atau kontak "Terbuka" atau "Tertutup" secara permanen.

Serangkaian aturan atau Hukum Ekspresi Aljabar Boolean telah diciptakan untuk membantu mengurangi jumlah gerbang logika yang diperlukan untuk melakukan operasi logika tertentu yang menghasilkan daftar fungsi atau teorema yang dikenal umum sebagai Hukum Aljabar Boolean.

Aljabar Boolean adalah matematika yang kami gunakan untuk menganalisis gerbang dan rangkaian digital. Kita dapat menggunakan "Hukum Boolean" ini untuk mengurangi dan menyederhanakan ekspresi Boolean yang kompleks dalam upaya untuk mengurangi jumlah gerbang logika yang diperlukan. Oleh karena itu Aljabar Boolean adalah sistem matematika yang didasarkan pada logika yang memiliki seperangkat aturan atau hukum yang digunakan untuk menentukan dan mengurangi ekspresi Boolean.

Variabel yang digunakan dalam Aljabar Boolean hanya memiliki satu dari dua nilai yang mungkin, logika "0" dan logika "1" tetapi ekspresi dapat memiliki jumlah variabel tak terbatas yang semuanya dilabeli secara individual untuk mewakili input ke ekspresi, Misalnya, variabel A, B, C dll, memberi kita ekspresi logika dari A + B = C, tetapi setiap variabel HANYA dapat berupa 0 atau berupa 1.

Contoh masing-masing hukum Boolean ini, aturan dan teorema untuk Aljabar Boolean diberikan dalam tabel berikut.

Tabel Kebenaran untuk Hukum Boolean

Dasar Hukum Aljabar Boolean yang berhubungan dengan Hukum Komutatif yang memungkinkan perubahan posisi untuk penambahan dan perkalian, Hukum Asosiatif yang memungkinkan penghapusan tanda kurung untuk penambahan dan perkalian, serta Hukum Distributif yang memungkinkan anjak piutang ekspresi, adalah sama seperti pada aljabar biasa.

Masing-masing Hukum Boolean di atas diberikan hanya dengan satu atau dua variabel, tetapi jumlah variabel yang didefinisikan oleh satu hukum tidak terbatas pada hal ini karena dapat ada jumlah variabel yang tak terbatas sebagai input juga ekspresi. Hukum Boolean yang dirinci di atas dapat digunakan untuk membuktikan ekspresi Boolean yang diberikan serta untuk menyederhanakan rangkain digital yang rumit.

Kemudian penjelasan singkat tentang berbagai Hukum Boolean akan diberikan di bawah ini dengan A yang mewakili input dari variabel.

Deskripsi Hukum Aljabar Boolean

Hukum Pembatalan- Istilah AND'ed dengan "0" sama dengan 0 atau OR'ed dengan "1" akan sama dengan 1

• A . 0 = 0  Sebuah variabel AND'ed dengan 0 selalu sama dengan 0
• A + 1 = 1  Sebuah variabel OR'ed dengan 1 selalu sama dengan 1

Hukum Identitas - Suatu istilah OR´d dengan "0" atau AND´ed dengan "1" akan selalu sama dengan istilah itu

• A + 0 = A  Sebuah variabel OR'ed dengan 0 selalu sama dengan variabel
• A . 1 = A  Sebuah variabel AND'ed dengan 1 selalu sama dengan variabel

Hukum Idempoten - Suatu input yang AND dan OR dengan itu sendiri sama dengan input itu

• A + A = A  Sebuah variabel OR'ed dengan dirinya sendiri selalu sama dengan variabel
• A . A = A  Sebuah variabel AND'ed dengan dirinya sendiri selalu sama dengan variabel

Hukum Komplemen - Suatu istilah AND´ed dengan pelengkapnya sama dengan "0" dan istilah OR dengan pelengkapnya sama dengan "1"

• A .  = 0  Sebuah variabel AND'ed dengan komplemennya selalu sama dengan 0
• A +  = 1  Sebuah variabel OR'ed dengan komplemennya selalu sama dengan 1

Hukum Komutatif - Urutan penerapan dua istilah yang terpisah tidak penting

• A . B = B . A Urutan di mana dua variabel AND'ed tidak membuat perbedaan
• A + B = B + A Urutan di mana dua variabel OR'ed tidak membuat perbedaan

Hukum Negasi Ganda - Suatu istilah yang terbalik dua kali sama dengan istilah aslinya

•  = A Sebuah komplemen ganda dari suatu variabel selalu sama dengan variabel

Teorema de Morgan - Ada dua aturan atau teorema "de Morgan",

1. Dua hal yang terpisah NOR'ed bersama-sama adalah sama dengan dua istilah terbalik (Complement) dan AND'ed misalnya:  =  . 
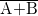2. Dua istilah terpisah NAND´ed bersama adalah sama dengan dua istilah terbalik (Komplemen) dan OR ´ed misalnya:  =  + .

Hukum aljabar lainnya dari Boolean yang tidak dirinci di atas termasuk:

Hukum Distributif - Hukum ini mengizinkan penggandaan atau pemfaktoran dari ekspresi.

• A (B + C) = A0B + A.C (Hukum Distributif OR)
• A + (B.C) = (A + B). (A + C) (Hukum Distribusi AND)

Hukum Absorptif (Penyerapan) - Hukum ini memungkinkan pengurangan dalam ekspresi yang rumit menjadi lebih sederhana dengan menyerap istilah-istilah yang serupa.

• A + (A.B) = A (Hukum Penyerapan OR)
• A (A + B) = A (Hukum Penyerapan AND)

Hukum Asosiatif - Hukum ini memungkinkan penghapusan tanda kurung dari ekspresi dan pengelompokan ulang variabel.

• A + (B + C) = (A + B) + C = A + B + C (Hukum Asosiasi OR)
• A (B.C) = (A.B) C = A. B C (Hukum Asosiasi AND)

Fungsi Aljabar Boolean

Dengan menggunakan informasi di atas, 2-input sederhana Gerbang AND, Gerbang OR dan Gerbang NOT dapat diwakili oleh 16 fungsi yang mungkin seperti yang ditunjukkan pada tabel berikut.

Fungsi	Deskripsi	Ekspresi
1.	BATAL	0
2.	IDENTITAS	1
3.	Input A	A
4.	Input B	B
5.	NOT A
6.	NOT B
7.	A AND B (AND)	A.B
8.	A AND NOT B	A.
9.	NOT A AND B	.B
10.	NOT AND (NAND)
11.	A OR B (OR)	A + B
12.	A OR NOT B	A +
13.	NOT A OR B	+ B
14.	NOT OR (NOR)
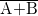15.	Eksklusif-OR	A. +  . B
16.	Eksklusif-NOR	A.B +  .

Contoh: Hukum Aljabar Boolean No.1

Menggunakan hukum di atas, sederhanakan ungkapan berikut: (A + B) (A + C)

Q =	(A + B).(A + C)
	A.A + A.C + A.B + B.C	- hukum distributif
	A + A.C + A.B + B.C	- hukum Idempotent AND (A.A = A)
	A(1 + C) + A.B + B.C	- hukum distributif
	A.1 + A.B + B.C	- hukum Identitas  OR (1 + C = 1)
	A(1 + B) + B.C	- hukum distributif
	A.1 + B.C	- hukum Identitas OR (1 + B = 1)
Q =	A + (B.C)	- hukum Identitas AND (A.1 = A)

Kemudian ungkapan: (A + B) (A + C) dapat disederhanakan menjadi A + (B.C) seperti dalam hukum Distributif.

Berbagi :