Osilator Jembatan Wien
Penggunaan Osilator Jembatan Wien menggunakan dua Jaringan RC yang terhubung bersama untuk menghasilkan osilator sinusoidal. Dalam tutorial Osilator RC kami melihat bahwa sejumlah resistor dan kapasitor dapat dihubungkan bersama dengan penguat inverting untuk menghasilkan rangkaian berosilasi.
Salah satu osilator gelombang sinusoidal sederhana yang menggunakan Jaringan RC sebagai pengganti Rangkaian LC konvensional untuk menghasilkan bentuk gelombang output sinusoidal, disebut Osilator Jembatan Wien.
Osilator Jembatan Wien disebut demikian karena rangkaian didasarkan pada bentuk frekuensi-selektif rangkaian Jembatan Wheatstone. Osilator Jembatan Wien adalah rangkaian penguat ditambah dua tahap RC yang memiliki stabilitas yang baik pada frekuensi resonan, distorsi rendah dan sangat mudah disetel menjadikannya rangkaian yang populer sebagai osilator frekuensi audio tetapi perubahan fasa dari sinyal output jauh berbeda dengan pergeseran fasa Osilator RC sebelumnya.
Osilator Jembatan Wien menggunakan rangkaian umpan balik yang terdiri dari serangkaian rangkaian RC terhubung dengan paralel RC dari nilai-nilai komponen yang sama menghasilkan rangkaian fasa delay atau fasa advanced tergantung pada frekuensi. Pada frekuensi resonansi atau pergeseran fasa adalah 0°. Pertimbangkan rangkaian di bawah ini.
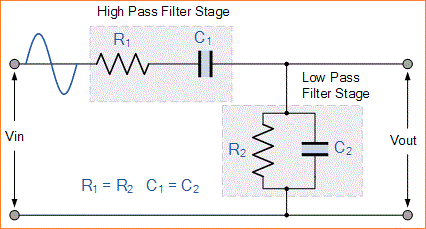
Jaringan RC di atas terdiri dari serangkaian rangkaian RC terhubung ke paralel RC membentuk dasarnya High Pass Filter terhubung ke Low Pass Filter menghasilkan frekuensi Orde-2 kedua sangat selektif tergantung Band Pass Filter dengan tinggi Q faktor di dipilih frekuensi, ƒr.
Pada frekuensi rendah, reaktansi kapasitor seri ( C1 ) sangat tinggi sehingga bekerja sedikit seperti rangkaian terbuka, menghalangi setiap sinyal input di Vin sehingga hampir tidak ada sinyal output, Vout. Demikian juga, pada frekuensi tinggi, reaktansi kapasitor paralel, ( C2 ) menjadi sangat rendah, sehingga kapasitor yang terhubung paralel ini bekerja sedikit seperti hubung singkat pada output, jadi sekali lagi tidak ada sinyal output.
Jadi harus ada titik frekuensi antara dua ekstrem C1 ini menjadi hubung-terbuka dan C2 hubung-pendek di mana tegangan output, VOUT mencapai nilai maksimumnya. Nilai frekuensi dari gelombang input di mana ini terjadi disebut osilator Frekuensi Resonansi, ( ƒr ).
Pada frekuensi resonansi ini, reaktansi rangkaian sama dengan resistannya, yaitu: Xc = R, dan perbedaan fasa antara input dan output sama dengan nol derajat. Oleh karena itu besarnya tegangan output pada maksimum dan sama dengan sepertiga (1/3) dari tegangan input seperti yang ditunjukkan.
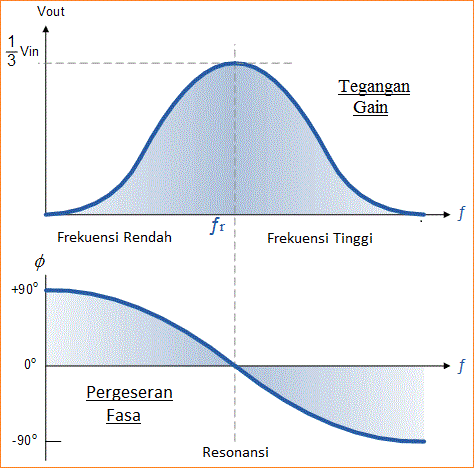
Dapat dilihat bahwa pada frekuensi yang sangat rendah, sudut fasa antara sinyal input dan output adalah "Positif" Fasa Lanjut (Phase Andvanced), sedangkan pada frekuensi yang sangat tinggi sudut fasa menjadi "Negatif" Fasa Keterlambatan (Phase Delay).
Di tengah-tengah kedua titik ini rangkaian berada pada frekuensi resonansinya, ( ƒr ) dengan dua sinyal “in-phase” atau 0°. Karena itu kita dapat mendefinisikan titik frekuensi resonansi ini dengan ekspresi berikut.
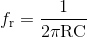
Dimana:
ƒr adalah Frekuensi Resonan dalam Hertz
R adalah Resistansi dalam Ohm
C adalah Kapasitansi dalam Farad
Kami mengatakan sebelumnya bahwa besarnya tegangan output, Vout dari jaringan RC berada pada nilai maksimum dan sama dengan sepertiga (1/3) dari tegangan input, Vin untuk memungkinkan terjadinya osilasi. Tapi mengapa sepertiga dan bukan nilai lain. Untuk memahami mengapa output dari rangkaian RC di atas harus sepertiga, yaitu 0.333xVin, kita harus mempertimbangkan impedansi kompleks ( Z = R ± jX ) dari dua rangkaian RC yang terhubung.
Kita tahu dari tutorial Teori Rangkaian AC bahwa bagian nyata dari impedansi kompleks adalah resistansi, R sedangkan bagian imajiner adalah reaktansi, X. Seperti kita berurusan dengan kapasitor di sini, bagian reaktansi akan reaktansi kapasitif, Xc.
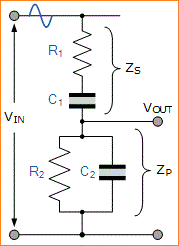
Jika kita menggambar ulang jaringan RC di atas seperti yang ditunjukkan, kita dapat dengan jelas melihat bahwa itu terdiri dari dua rangkaian RC yang terhubung bersama dengan output yang diambil dari persimpangan mereka. Resistor R1 dan kapasitor C1 membentuk jaringan seri atas, sedangkan resistor R2 dan kapasitor C2 membentuk jaringan paralel bawah.
Oleh karena itu total impedansi DC dari kombinasi seri ( R1 C1 ) kita dapat memanggil, ZS dan impedansi total kombinasi paralel ( R2 C2 ) kita dapat memanggil, ZP. Sebagai ZS dan ZP secara efektif dihubungkan bersama dalam seri di input, VIN, mereka membentuk jaringan pembagi tegangan dengan output diambil dari seberang ZP seperti yang ditunjukkan.
Mari kita berasumsi kemudian bahwa nilai-nilai komponen R1 dan R2 adalah sama di: 12kΩ, kapasitor C1 dan C2 adalah sama di: 3.9nF dan frekuensi pasokan, ƒ adalah 3.4kHz.
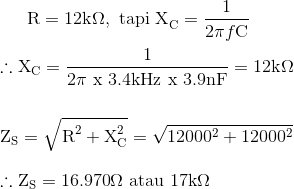
Kita sekarang tahu bahwa dengan frekuensi supply 3.4 kHz, reaktansi kapasitor sama dengan resistansi resistor pada 12 kΩ. Ini kemudian memberi kita impedansi seri atas ZS dari 17kΩ.
Untuk lebih rendah paralel impedansi ZP, sebagai dua komponen yang secara paralel, kita harus memperlakukan ini berbeda karena impedansi dari rangkaian paralel dipengaruhi oleh kombinasi paralel ini.
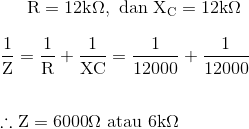
Pada frekuensi supply 3400Hz, atau 3.4 kHz, impedansi DC gabungan dari rangkaian RC paralel menjadi 6kΩ (R||Xc ) dengan jumlah vektor impedansi paralel ini dihitung sebagai:
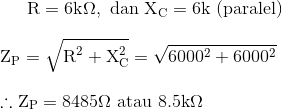
Jadi kita sekarang memiliki nilai untuk jumlah vektor dari impedansi seri: 17kΩ, (ZS = 17kΩ) dan untuk impedansi paralel: 8.5kΩ, (ZP = 8.5kΩ). Oleh karena itu total impedansi output, Zout dari jaringan pembagi tegangan pada frekuensi yang diberikan adalah:
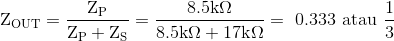
Kemudian pada frekuensi osilasi, besarnya tegangan output, Vout akan sama dengan Zout x Vin yang seperti ditunjukkan sama dengan sepertiga (1/3) dari tegangan input, Vin dan itu adalah jaringan RC selektif frekuensi ini yang membentuk dasar dari rangkaian Osilator Jembatan Wien.
Jika sekarang kita menempatkan Jaringan RC ini pada Penguat Non-Inverting yang memiliki gain 1 + R1/R2, rangkaian osilator jembatan Wien dasar berikut ini diproduksi.
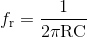
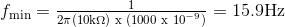
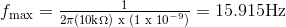

Frekuensi osilasi untuk Osilator Jembatan Wien diberikan sebagai 5200 Hertz. Jika resistor R1 = R2 dan kapasitor C1 = C2 dan kami mengasumsikan nilai untuk kapasitor umpan balik 3.0nF, maka nilai yang sesuai dari resistor umpan balik dihitung sebagai:
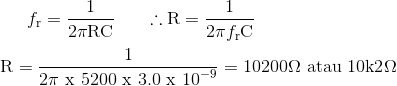
Agar osilasi sinusoidal dimulai, gain tegangan dari rangkaian Jembatan Wien harus sama atau lebih besar dari 3, ( Av ≥ 3 ). Untuk konfigurasi Op-amp non-inverting, nilai ini ditetapkan oleh jaringan resistor umpan balik R3 dan R4 dan diberikan sebagai:
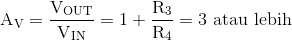
Jika kita memilih nilai untuk resistor R3 katakanlah, 100kΩ, maka nilai resistor R4 dihitung sebagai:
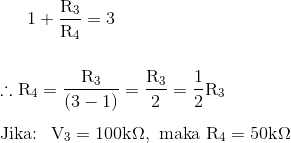
Sementara gain 3 adalah nilai minimum yang diperlukan untuk memastikan osilasi, pada kenyataannya nilai sedikit lebih tinggi dari yang biasanya diperlukan. Jika kita mengasumsikan nilai gain 3.1 maka resistor R4 dihitung ulang untuk memberikan nilai 47kΩ. Ini memberi rangkaian Osilator Jembatan Wien terakhir sebagai:
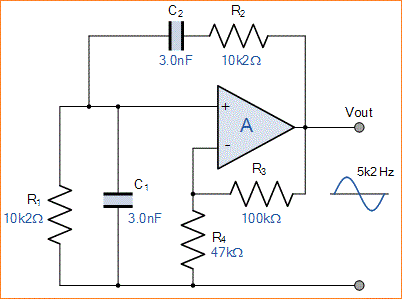
Salah satu osilator gelombang sinusoidal sederhana yang menggunakan Jaringan RC sebagai pengganti Rangkaian LC konvensional untuk menghasilkan bentuk gelombang output sinusoidal, disebut Osilator Jembatan Wien.
Osilator Jembatan Wien disebut demikian karena rangkaian didasarkan pada bentuk frekuensi-selektif rangkaian Jembatan Wheatstone. Osilator Jembatan Wien adalah rangkaian penguat ditambah dua tahap RC yang memiliki stabilitas yang baik pada frekuensi resonan, distorsi rendah dan sangat mudah disetel menjadikannya rangkaian yang populer sebagai osilator frekuensi audio tetapi perubahan fasa dari sinyal output jauh berbeda dengan pergeseran fasa Osilator RC sebelumnya.
Osilator Jembatan Wien menggunakan rangkaian umpan balik yang terdiri dari serangkaian rangkaian RC terhubung dengan paralel RC dari nilai-nilai komponen yang sama menghasilkan rangkaian fasa delay atau fasa advanced tergantung pada frekuensi. Pada frekuensi resonansi atau pergeseran fasa adalah 0°. Pertimbangkan rangkaian di bawah ini.
Pergeseran Fasa Jaringan RC

Jaringan RC di atas terdiri dari serangkaian rangkaian RC terhubung ke paralel RC membentuk dasarnya High Pass Filter terhubung ke Low Pass Filter menghasilkan frekuensi Orde-2 kedua sangat selektif tergantung Band Pass Filter dengan tinggi Q faktor di dipilih frekuensi, ƒr.
Pada frekuensi rendah, reaktansi kapasitor seri ( C1 ) sangat tinggi sehingga bekerja sedikit seperti rangkaian terbuka, menghalangi setiap sinyal input di Vin sehingga hampir tidak ada sinyal output, Vout. Demikian juga, pada frekuensi tinggi, reaktansi kapasitor paralel, ( C2 ) menjadi sangat rendah, sehingga kapasitor yang terhubung paralel ini bekerja sedikit seperti hubung singkat pada output, jadi sekali lagi tidak ada sinyal output.
Jadi harus ada titik frekuensi antara dua ekstrem C1 ini menjadi hubung-terbuka dan C2 hubung-pendek di mana tegangan output, VOUT mencapai nilai maksimumnya. Nilai frekuensi dari gelombang input di mana ini terjadi disebut osilator Frekuensi Resonansi, ( ƒr ).
Pada frekuensi resonansi ini, reaktansi rangkaian sama dengan resistannya, yaitu: Xc = R, dan perbedaan fasa antara input dan output sama dengan nol derajat. Oleh karena itu besarnya tegangan output pada maksimum dan sama dengan sepertiga (1/3) dari tegangan input seperti yang ditunjukkan.
Gain Output Osilator dan Pergeseran fasa

Dapat dilihat bahwa pada frekuensi yang sangat rendah, sudut fasa antara sinyal input dan output adalah "Positif" Fasa Lanjut (Phase Andvanced), sedangkan pada frekuensi yang sangat tinggi sudut fasa menjadi "Negatif" Fasa Keterlambatan (Phase Delay).
Di tengah-tengah kedua titik ini rangkaian berada pada frekuensi resonansinya, ( ƒr ) dengan dua sinyal “in-phase” atau 0°. Karena itu kita dapat mendefinisikan titik frekuensi resonansi ini dengan ekspresi berikut.
Frekuensi Osilator Jembatan Wien
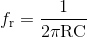
Dimana:
ƒr adalah Frekuensi Resonan dalam Hertz
R adalah Resistansi dalam Ohm
C adalah Kapasitansi dalam Farad
Kami mengatakan sebelumnya bahwa besarnya tegangan output, Vout dari jaringan RC berada pada nilai maksimum dan sama dengan sepertiga (1/3) dari tegangan input, Vin untuk memungkinkan terjadinya osilasi. Tapi mengapa sepertiga dan bukan nilai lain. Untuk memahami mengapa output dari rangkaian RC di atas harus sepertiga, yaitu 0.333xVin, kita harus mempertimbangkan impedansi kompleks ( Z = R ± jX ) dari dua rangkaian RC yang terhubung.
Kita tahu dari tutorial Teori Rangkaian AC bahwa bagian nyata dari impedansi kompleks adalah resistansi, R sedangkan bagian imajiner adalah reaktansi, X. Seperti kita berurusan dengan kapasitor di sini, bagian reaktansi akan reaktansi kapasitif, Xc.
Jaringan RC

Oleh karena itu total impedansi DC dari kombinasi seri ( R1 C1 ) kita dapat memanggil, ZS dan impedansi total kombinasi paralel ( R2 C2 ) kita dapat memanggil, ZP. Sebagai ZS dan ZP secara efektif dihubungkan bersama dalam seri di input, VIN, mereka membentuk jaringan pembagi tegangan dengan output diambil dari seberang ZP seperti yang ditunjukkan.
Mari kita berasumsi kemudian bahwa nilai-nilai komponen R1 dan R2 adalah sama di: 12kΩ, kapasitor C1 dan C2 adalah sama di: 3.9nF dan frekuensi pasokan, ƒ adalah 3.4kHz.
Rangkaian Seri
Impedansi total kombinasi seri dengan resistor, R1 dan kapasitor, C1 adalah sederhana: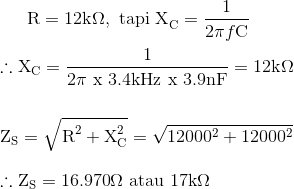
Untuk lebih rendah paralel impedansi ZP, sebagai dua komponen yang secara paralel, kita harus memperlakukan ini berbeda karena impedansi dari rangkaian paralel dipengaruhi oleh kombinasi paralel ini.
Rangkaian Paralel
Total impedansi dari kombinasi paralel lebih rendah dengan resistor, R2 dan kapasitor, C2 diberikan sebagai: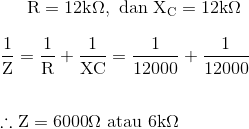
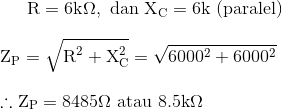
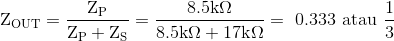
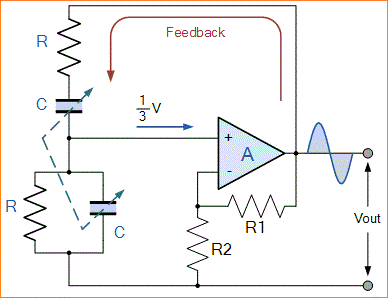
Jika sekarang kita menempatkan Jaringan RC ini pada Penguat Non-Inverting yang memiliki gain 1 + R1/R2, rangkaian osilator jembatan Wien dasar berikut ini diproduksi.
Rangkaian Osilator Jembatan Wien

Output dari penguat operasional (Op-amp) diumpankan kembali ke kedua input penguat. Salah satu bagian dari sinyal umpan balik dihubungkan ke terminal input Inverting (umpan balik negatif atau degeneratif) melalui jaringan pembagi resistor R1 dan R2 yang memungkinkan kenaikan tegangan gain disesuaikan dalam batas sempit.
Bagian lain, yang membentuk kombinasi seri dan paralel dari R dan C membentuk jaringan umpan balik dan diumpankan kembali ke terminal input non-inverting (umpan balik positif atau regeneratif) melalui jaringan RC Jembatan Wien dan kombinasi umpan balik positif inilah yang menimbulkan osilasi.
Jaringan RC terhubung dalam jalur umpan balik positif dari penguat dan memiliki pergeseran fasa nol hanya satu frekuensi. Kemudian pada frekuensi resonansi yang dipilih, ( ƒr ) tegangan yang diterapkan pada input Penguat Inverting dan Penguat Non-inverting akan sama dan “dalam-fasa” sehingga umpan balik positif akan membatalkan sinyal umpan balik negatif yang menyebabkan rangkaian berosilasi.
Gain tegangan dari rangkaian penguat HARUS sama atau lebih besar dari tiga "Gain = 3" untuk memulai osilasi karena seperti yang telah kita lihat di atas, inputnya adalah 1/3 dari output. Nilai ini, ( Av ≥ 3 ) ditetapkan oleh jaringan resistor umpan balik, R1 dan R2 dan untuk penguat non-inverting ini diberikan sebagai rasio 1+ (R1/R2).
Selain itu, karena batasan gain loop terbuka dari Op-amp, frekuensi di atas 1MHz tidak dapat diraih tanpa menggunakan Op-amp frekuensi tinggi khusus.
Contoh: Osilator Jembatan Wien No.1
Menentukan frekuensi maksimum dan minimum osilasi dari rangkaian Osilator Jembatan Wien memiliki resistor 10kΩ dan kapasitor variabel 1NF ke 1000nF.
Frekuensi osilasi untuk Osilator Jembatan Wien diberikan sebagai:
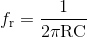
Frekuensi Terendah Osilator Jembatan Wien
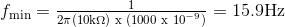
Frekuensi Tertinggi Osilator Jembatan Wien
Contoh: Osilator Jembatan Wien No.2
Sebuah rangkaian Osilator Jembatan Wien diperlukan untuk menghasilkan bentuk gelombang sinusoidal dari 5.200 Hertz (5.2kHz). Menghitung nilai-nilai frekuensi menentukan Resistor R1 dan R2 dan dua Kapasitor C1 dan C2 untuk menghasilkan frekuensi yang diperlukan.
Juga, jika rangkaian osilator didasarkan pada konfigurasi Op-amp non-inverting, tentukan nilai minimum untuk resistor gain untuk menghasilkan osilasi yang diperlukan. Akhirnya gambarlah rangkaian osilator yang dihasilkan.

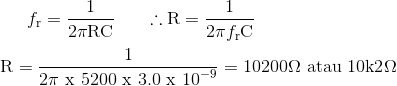
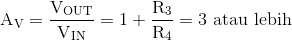
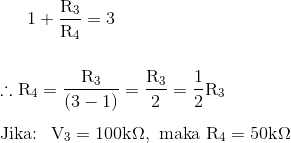
Rangkaian Osilator Jembatan Wien

Ringkasan Osilator Jembatan Wien
Kemudian agar osilasi terjadi dalam rangkaian Osilator Jembatan Wien, kondisi berikut harus berlaku.
- Tanpa sinyal input, Osilator Jembatan Wien menghasilkan osilasi output kontinu.
- Osilator Jembatan Wien dapat menghasilkan berbagai frekuensi.
- Gain Tegangan penguat amplifier harus lebih besar dari 3.
- Jaringan RC dapat digunakan dengan Op-amp Non-Inverting.
- Resistansi input penguat (amplifier) harus tinggi dibandingkan dengan R sehingga Jaringan RC tidak kelebihan beban dan mengubah kondisi yang diperlukan.
- Resistansi output penguat harus rendah sehingga efek pembebanan eksternal diminimalkan.
- Beberapa metode untuk menstabilkan amplitudo osilasi harus disediakan. Jika kenaikan tegangan penguat terlalu kecil osilasi yang diinginkan akan membusuk dan berhenti. Jika terlalu besar output akan memenuhi nilai rel dan distorsi supply.
- Dengan stabilisasi amplitudo dalam bentuk dioda feedback (umpan-balik), osilasi dari Osilator Jembatan Wien dapat berlanjut tanpa batas waktu.
Dalam tampilan akhir kami di Osilator, kami akan melihat Osilator Crystal yang menggunakan kristal kuarsa sebagai rangkaian tangki untuk menghasilkan frekuensi tinggi dan bentuk gelombang sinusoidal yang sangat stabil.