Transformasi Star-Delta dan Transformasi Delta-Star
Transformasi Star-Delta dan Transformasi Delta-Star memungkinkan kita untuk mengubah impedansi yang dihubungkan bersama dalam konfigurasi 3 fasa dari satu jenis koneksi ke yang lain.
Kita sekarang dapat memecahkan seri sederhana, paralel atau jenis jembatan jaringan resistif menggunakan Hukum Kirchoff Rangkaian, Analisis Arus Mesh atau teknik Analisis Tegangan Nodal tetapi dalam rangkaian 3-fasa seimbang kita dapat menggunakan teknik matematika yang berbeda untuk menyederhanakan analisis rangkaian dan dengan demikian mengurangi penggunaan matematika yang terlibat yang dengan sendirinya adalah hal yang baik.
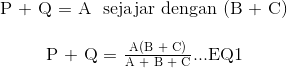
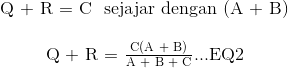
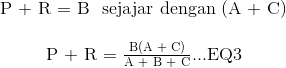
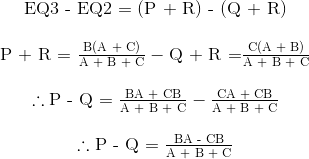

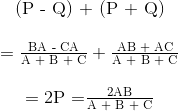
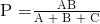
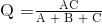
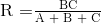
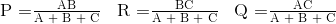
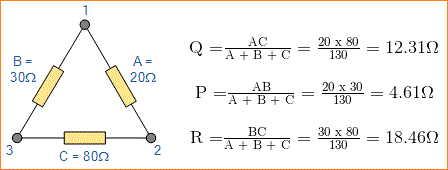
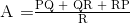
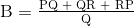
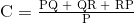

Kita sekarang dapat memecahkan seri sederhana, paralel atau jenis jembatan jaringan resistif menggunakan Hukum Kirchoff Rangkaian, Analisis Arus Mesh atau teknik Analisis Tegangan Nodal tetapi dalam rangkaian 3-fasa seimbang kita dapat menggunakan teknik matematika yang berbeda untuk menyederhanakan analisis rangkaian dan dengan demikian mengurangi penggunaan matematika yang terlibat yang dengan sendirinya adalah hal yang baik.
Rangkaian atau jaringan 3 fasa standar menggunakan dua bentuk utama dengan nama yang mewakili cara di mana resistansi dihubungkan, jaringan terhubung Star yang memiliki simbol huruf, Υ (wye) dan jaringan terhubung Delta yang memiliki simbol sebuah segitiga, ∆ (delta).
Jika supply 3-fasa, 3-kawat atau bahkan 3-fasa terhubung dalam satu jenis konfigurasi, dapat dengan mudah diubah atau transformasi menjadi konfigurasi yang setara dengan jenis lainnya dengan menggunakan Transformasi Star Delta atau Proses Transformasi Star Delta.
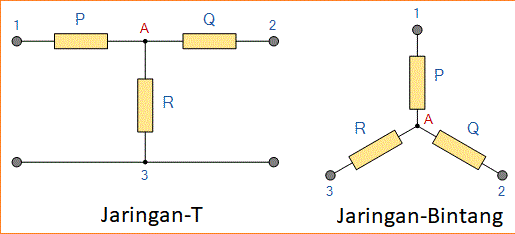
Sebuah jaringan resistif terdiri dari tiga impedansi dapat dihubungkan bersama untuk membentuk T atau konfigurasi “Tee” tetapi jaringan juga dapat digambar ulang untuk membentuk Star atau Υ jenis jaringan seperti yang ditunjukkan di bawah ini.
T-terhubung dan Jaringan Star Ekuivalen

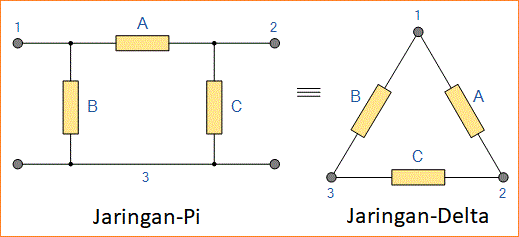
Seperti yang telah kita lihat, kita dapat redraw T jaringan resistor di atas untuk menghasilkan setara elektrik Star atau Υ jenis jaringan. Tapi kita juga bisa mengkonversi Pi atau π jenis jaringan resistor menjadi setara listrik Delta atau ∆ jenis jaringan seperti yang ditunjukkan di bawah ini.
Pi-terhubung dan Jaringan Delta Ekuivalen

Setelah sekarang didefinisikan apa yang disebut Star dan Delta terhubung jaringan adalah mungkin untuk mengubah rangkaian Υ menjadi setara ∆ dan juga untuk mengkonversi rangkaian ∆ menjadi setara Υ menggunakan proses transformasi.
Proses ini memungkinkan kita untuk menghasilkan hubungan matematis antara berbagai resistor yang memberi kita Transformasi Star Delta serta Transformasi Delta Star. Transformasi rangkaian ini memungkinkan kita untuk mengubah tiga resistansi yang terhubung (atau impedansi) dengan ekuivalennya yang diukur antara terminal 1-2, 1-3 atau 2-3 untuk rangkaian yang terhubung dengan Star atau Delta.
Namun, jaringan yang dihasilkan hanya setara untuk tegangan dan arus eksternal ke jaringan star atau delta, karena secara internal tegangan dan arus berbeda tetapi masing-masing jaringan akan mengkonsumsi jumlah daya yang sama dan memiliki faktor daya yang sama satu sama lain.
Transformasi Delta Star
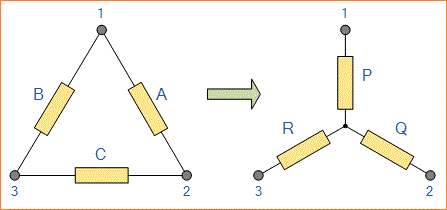
Untuk mengonversi jaringan delta ke jaringan star yang setara, kita perlu menurunkan rumus transformasi untuk menyamakan berbagai resistor satu sama lain di antara berbagai terminal. Pertimbangkan rangkaian di bawah ini.
Transformasi Jaringan Delta ke Star

Bandingkan resistansi antara terminal 1 dan 2.
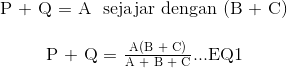
Resistansi antara terminal 2 dan 3.
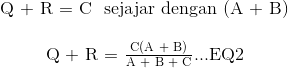
Resistansi antara terminal 1 dan 3.
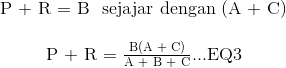
Ini sekarang memberi kita tiga persamaan dan mengambil persamaan 3 dari persamaan 2 memberi:
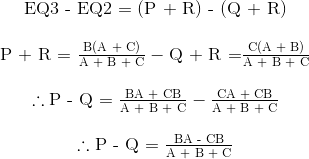
Kemudian, menulis ulang Persamaan 1 akan memberi kita:

Menambahkan bersama persamaan 1 dan hasil di atas dari persamaan 3 dikurangi persamaan 2 memberikan:
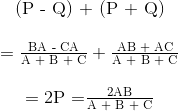
Dari yang memberi kita persamaan akhir untuk resistor P sebagai:
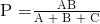
Kemudian untuk merangkum sedikit tentang matematika di atas, kita sekarang dapat mengatakan bahwa resistor P dalam jaringan Star dapat ditemukan sebagai Persamaan 1 plus (Persamaan 3 dikurangi Persamaan 2) atau Eq1 + (Eq3 - Eq2).
Demikian pula, untuk menemukan resistor Q dalam jaringan Star, adalah persamaan 2 ditambah hasil persamaan 1 minus persamaan 3 atau Eq2 + (Eq1 - Eq3) dan ini memberi kita transformasi Q sebagai:
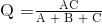
dan lagi, untuk menemukan resistor R dalam jaringan Star, adalah persamaan 3 ditambah hasil persamaan 2 minus persamaan 1 atau Eq3 + (Eq2 - Eq1) dan ini memberi kita transformasi R sebagai:
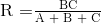
Ketika mengubah jaringan delta menjadi jaringan Star, penyebut semua rumus transformasi adalah sama: A + B + C, dan yang merupakan jumlah dari SEMUA resistansi delta. Kemudian untuk mengonversi jaringan yang terhubung delta ke jaringan star yang setara, kita dapat meringkas persamaan transformasi di atas sebagai:
Persamaan Transformasi Delta ke Star
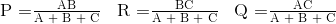
Jika tiga Resistor dalam jaringan delta semuanya sama nilainya maka resistor yang dihasilkan dalam jaringan star ekuivalen akan sama dengan sepertiga nilai resistor delta. Ini memberi setiap cabang resistif dalam jaringan star nilai: RSTAR = 1/3*RDELTA yang sama dengan mengatakan: (RDELTA)/3
Contoh: Transformasi Delta - Star No.1
Ubah Jaringan Resistif Delta berikut menjadi Jaringan Star yang ekuivalen/setara.
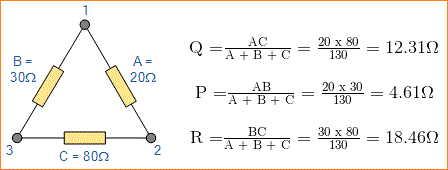
Transformasi Star Delta
Transformasi Star Delta hanyalah kebalikan dari di atas. Kita telah melihat bahwa ketika mengkonversi dari jaringan delta ke jaringan star ekuivalen yang resistor terhubung ke satu terminal adalah hasil dari dua resistansi delta yang terhubung ke terminal yang sama, misalnya resistor P adalah hasil resistor A dan B yang terhubung ke terminal 1.
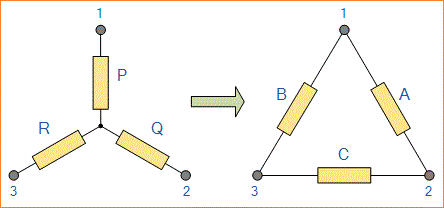
Dengan menulis ulang rumus sebelumnya sedikit kita juga dapat menemukan rumus transformasi untuk mengubah jaringan star resistif ke jaringan delta yang setara memberi kita cara menghasilkan transformasi star delta seperti yang ditunjukkan di bawah ini.
Transformasi Jaringan Star ke Delta

Nilai resistor pada salah satu sisi jaringan delta, ∆ adalah jumlah dari semua kombinasi dua hasil resistor dalam jaringan star yang dibagi oleh resistor star yang terletak “berhadapan langsung” dengan resistor delta yang ditemukan. Misalnya, resistor A diberikan sebagai:
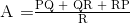
sehubungan dengan terminal 3 dan resistor B diberikan sebagai:
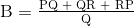
sehubungan dengan terminal 2 dengan resistor C diberikan sebagai:
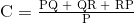
sehubungan dengan terminal 1.
Dengan membagi setiap persamaan dengan nilai penyebut kita berakhir dengan tiga rumus transformasi terpisah yang dapat digunakan untuk mengubah jaringan resistif Delta menjadi jaringan Star yang setara seperti yang diberikan di bawah ini.
Persamaan Transformasi Star Delta

Satu poin terakhir tentang mengkonversi jaringan resistif star ke jaringan delta yang setara. Jika semua resistor dalam jaringan Star semuanya sama nilainya maka resistor yang dihasilkan dalam jaringan delta ekuivalen akan tiga kali nilai resistor star dan sama, memberikan: RDELTA = 3*RSTAR
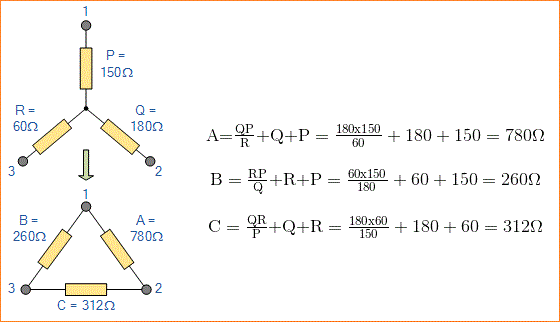
Contoh: Star - Delta No.2
Ubah Jaringan Resistif Star berikut menjadi Jaringan Delta yang setara.

Kedua Transformasi Star Delta dan Transformasi Delta Star memungkinkan kita untuk mengkonversi salah satu jenis koneksi rangkaian ke jenis lain dalam rangka bagi kita untuk dengan mudah menganalisis rangkaian. Teknik-teknik transformasi ini dapat digunakan untuk efek yang baik untuk rangkaian star atau delta yang mengandung resistansi atau impedansi.