Teorema Norton
Teorema Norton adalah metode analisis yang digunakan untuk mengubah rangkaian kompleks menjadi rangkaian ekuivalen sederhana yang terdiri dari resistor tunggal secara paralel dengan sumber arus.
Dalam beberapa hal, Teorema Norton dapat dianggap sebagai kebalikan dari "Teorema Thevenin" yang sudah kami bahas sebelumnya, dalam hal itu Thevenin mengurangi rangkaiannya menjadi satu resistor secara seri dengan tegangan tunggal. Norton di sisi lain mengurangi rangkaiannya menjadi satu resistor paralel dengan sumber arus konstan.
Pernyataan Teorema Norton yaitu “ Pada setiap rangkaian linear yang memiliki beberapa sumber energi dan resistansi/hambatan bisa diganti dengan generator Arus Konstan tunggal terhubung paralel dengan Resistor Tunggal “.
Resistor beban, RL yang bersangkutan resistor single ini, RS adalah nilai resistor melihat kembali ke dalam jaringan dengan semua arus source dan IS adalah arus terhubungan pendek di terminal output seperti yang ditunjukkan di bawah ini .
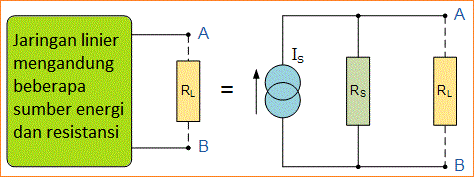
Nilai dari "arus konstan" ini adalah yang akan mengalir jika dua terminal output di mana disingkat bersamaan sedangkan resistor sumber akan diukur dengan melihat kembali ke terminal, (sama seperti Teorema Thevenin).
Sebagai contoh, perhatikan rangkaian kita sekarang familiar dari bagian sebelumnya.

Untuk menemukan persamaan Norton dari rangkaian di atas, pertama-tama kita harus melepas resistor beban pusat 40Ω dan menyingkat terminal A dan B untuk memberi kita rangkaian berikut.
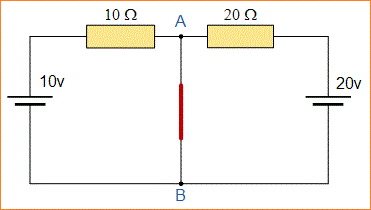
Ketika terminal A dan B disingkat menjadi dua resistor terhubung secara paralel di kedua sumber tegangan masing-masing dan arus yang mengalir melalui masing-masing resistor serta total arus hubung singkat sekarang dapat dihitung sebagai:
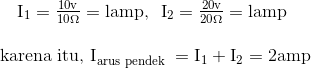
Jika kita menyingkat dua sumber tegangan dan terminal rangkaian terbuka A dan B, kedua resistor sekarang secara efektif terhubung bersama secara paralel. Nilai resistor internal Rs ditemukan dengan menghitung resistor total pada terminal A dan B yang memberi kita rangkaian berikut.
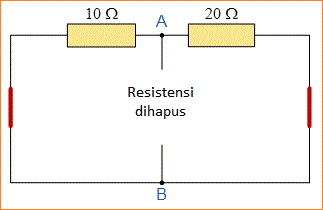
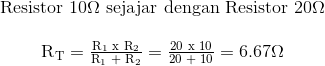
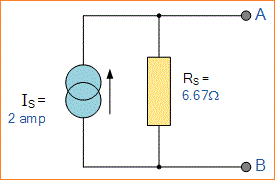
Setelah menemukan baik arus hubung singkat, Is dan resistansi internal yang setara, Rs ini kemudian memberi kita Rangkaian Norton ekuivalen berikut.
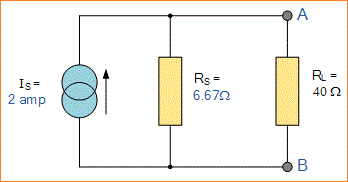
Ok, sejauh ini sangat baik, tetapi kita sekarang harus menyelesaikan dengan resistor beban 40Ω asli yang terhubung di terminal A dan B seperti yang ditunjukkan di bawah ini.
Sekali lagi, dua resistor dihubungkan secara paralel di terminal A dan B yang memberi kita hambatan total:
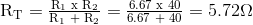
Tegangan melintasi terminal A dan B dengan resistor beban terhubung diberikan sebagai:
Kemudian arus yang mengalir dalam resistor beban 40Ω dapat ditemukan sebagai:

yang lagi-lagi, adalah nilai yang sama dengan 0.286 amp, kami temukan menggunakan Hukum Kirchhoff Rangkaian dalam tutorial sebelumnya.
1. Lepaskan resistor beban RL atau komponen yang bersangkutan.
2. Temukan RS dengan cara menyingkat semua sumber tegangan atau dengan membuka semua sumber arus.
3. Cari IS dengan menempatkan shorting link pada terminal output A dan B.
4. Cari arus yang mengalir melalui resistor beban RL.
Dalam sebuah rangkaian, daya yang disupply ke beban maksimal saat resistor beban sama dengan resistor sumber. Dalam tutorial berikutnya kita akan melihat Transfer Daya Maksimum.
Penerapan teorema transfer daya maksimum dapat diterapkan pada rangkaian linier sederhana dan rumit yang memiliki beban variabel dan digunakan untuk menemukan resistor beban yang mengarah pada transfer daya maksimum ke beban.
Dalam beberapa hal, Teorema Norton dapat dianggap sebagai kebalikan dari "Teorema Thevenin" yang sudah kami bahas sebelumnya, dalam hal itu Thevenin mengurangi rangkaiannya menjadi satu resistor secara seri dengan tegangan tunggal. Norton di sisi lain mengurangi rangkaiannya menjadi satu resistor paralel dengan sumber arus konstan.
Pernyataan Teorema Norton yaitu “ Pada setiap rangkaian linear yang memiliki beberapa sumber energi dan resistansi/hambatan bisa diganti dengan generator Arus Konstan tunggal terhubung paralel dengan Resistor Tunggal “.
Resistor beban, RL yang bersangkutan resistor single ini, RS adalah nilai resistor melihat kembali ke dalam jaringan dengan semua arus source dan IS adalah arus terhubungan pendek di terminal output seperti yang ditunjukkan di bawah ini .
Rangkaian Norton Ekuivalen

Nilai dari "arus konstan" ini adalah yang akan mengalir jika dua terminal output di mana disingkat bersamaan sedangkan resistor sumber akan diukur dengan melihat kembali ke terminal, (sama seperti Teorema Thevenin).
Sebagai contoh, perhatikan rangkaian kita sekarang familiar dari bagian sebelumnya.

Untuk menemukan persamaan Norton dari rangkaian di atas, pertama-tama kita harus melepas resistor beban pusat 40Ω dan menyingkat terminal A dan B untuk memberi kita rangkaian berikut.

Ketika terminal A dan B disingkat menjadi dua resistor terhubung secara paralel di kedua sumber tegangan masing-masing dan arus yang mengalir melalui masing-masing resistor serta total arus hubung singkat sekarang dapat dihitung sebagai:
Rangkaian Norton dengan A-B Shorted Out
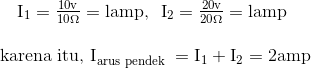
Jika kita menyingkat dua sumber tegangan dan terminal rangkaian terbuka A dan B, kedua resistor sekarang secara efektif terhubung bersama secara paralel. Nilai resistor internal Rs ditemukan dengan menghitung resistor total pada terminal A dan B yang memberi kita rangkaian berikut.

Mencari Resistor Ekuivalen/Setara (Rs)
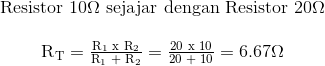
Setelah menemukan baik arus hubung singkat, Is dan resistansi internal yang setara, Rs ini kemudian memberi kita Rangkaian Norton ekuivalen berikut.
Rangkaian Akhir Norton Ekuivalen

Ok, sejauh ini sangat baik, tetapi kita sekarang harus menyelesaikan dengan resistor beban 40Ω asli yang terhubung di terminal A dan B seperti yang ditunjukkan di bawah ini.

Sekali lagi, dua resistor dihubungkan secara paralel di terminal A dan B yang memberi kita hambatan total:
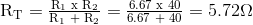
Tegangan melintasi terminal A dan B dengan resistor beban terhubung diberikan sebagai:
VA-B = I x R = 2 x 5.72 = 11.44v

yang lagi-lagi, adalah nilai yang sama dengan 0.286 amp, kami temukan menggunakan Hukum Kirchhoff Rangkaian dalam tutorial sebelumnya.
Ringkasan Teorema Norton
Prosedur dasar untuk menyelesaikan rangkaian menggunakan Teorema Norton adalah sebagai berikut:1. Lepaskan resistor beban RL atau komponen yang bersangkutan.
2. Temukan RS dengan cara menyingkat semua sumber tegangan atau dengan membuka semua sumber arus.
3. Cari IS dengan menempatkan shorting link pada terminal output A dan B.
4. Cari arus yang mengalir melalui resistor beban RL.
Dalam sebuah rangkaian, daya yang disupply ke beban maksimal saat resistor beban sama dengan resistor sumber. Dalam tutorial berikutnya kita akan melihat Transfer Daya Maksimum.
Penerapan teorema transfer daya maksimum dapat diterapkan pada rangkaian linier sederhana dan rumit yang memiliki beban variabel dan digunakan untuk menemukan resistor beban yang mengarah pada transfer daya maksimum ke beban.