Gelombang Harmonik
Gelombang Harmonik adalah frekuensi yang lebih tinggi yang tidak diinginkan yang ditumpangkan pada bentuk gelombang fundamental menciptakan pola gelombang terdistorsi. Dalam rangkaian AC, resistansi berperilaku dengan cara yang persis sama seperti pada rangkaian DC. Artinya, arus yang mengalir melalui resistansi sebanding dengan tegangan yang melewatinya.
Ini karena Resistor adalah perangkat linier dan jika tegangan yang diterapkan adalah gelombang sinus, arus yang mengalir melalui itu juga merupakan gelombang sinus sehingga perbedaan fasa antara kedua gelombang sinusoidal adalah nol.
Secara umum ketika berhadapan dengan tegangan dan arus bolak-balik dalam rangkaian listrik, diasumsikan bahwa mereka murni dan berbentuk gelombang sinusoidal dengan hanya satu nilai frekuensi, yang disebut "frekuensi fundamental" yang ada, tetapi ini tidak selalu terjadi.
Dalam perangkat atau rangkaian listrik atau elektronik yang memiliki karakteristik tegangan-arus yang tidak linier, yaitu arus yang mengalir melalui itu tidak sebanding dengan tegangan yang diberikan.
Bentuk gelombang bolak-balik yang terkait dengan perangkat akan berbeda hingga lebih besar atau lebih kecil daripada bentuk gelombang sinusoidal yang ideal. Jenis-jenis gelombang ini biasanya disebut sebagai bentuk gelombang non-sinusoidal atau kompleks.
Bentuk gelombang kompleks dihasilkan oleh perangkat listrik umum seperti Induktor berinti besi, Transformator switching, balast elektronik dalam lampu pijar dan beban induktif lainnya serta tegangan output dan bentuk gelombang arus dari alternator AC, generator dan mesin listrik lainnya. Hasilnya adalah bahwa bentuk arus mungkin tidak gelombang sinusoidal meskipun bentuk gelombang tegangan.
Juga sebagian besar rangkaian switching catu daya elektronik seperti Penyearah, Thyristor, Transistor daya, konverter daya dan SSR (solid state relay) lainnya yang memutus dan memotong catu daya gelombang sinusoidal untuk mengendalikan daya motor, atau mengubah catu daya sinusoidal AC ke DC.
Rangkaian pengalihan tesis ini cenderung menarik arus hanya pada nilai puncak dari supply AC dan karena bentuk gelombang pengalihan non-sinusoidal, maka arus beban yang dihasilkan dikatakan mengandung Harmonik.
Bentuk gelombang kompleks non-sinusoidal dibangun dengan "menambahkan" bersama-sama serangkaian frekuensi gelombang sinus yang dikenal sebagai "Harmonik". Harmonik adalah istilah umum yang digunakan untuk menggambarkan distorsi bentuk gelombang sinusoidal oleh bentuk gelombang frekuensi yang berbeda.
Lalu apa pun bentuknya, bentuk gelombang yang kompleks dapat dipecah secara matematis menjadi komponen-komponen individualnya yang disebut frekuensi dasar dan sejumlah "frekuensi harmonik". Tetapi apa yang kita maksud dengan “frekuensi dasar”.
Mari kita perhatikan bentuk frekuensi dasar atau gelombang AC 1 harmonik seperti yang ditunjukkan.
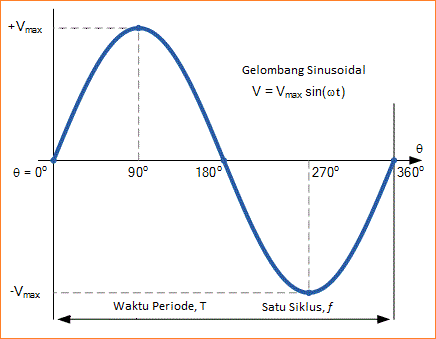
Di mana: Vmax adalah nilai puncak dalam volt dan ƒ adalah frekuensi bentuk gelombang dalam Hertz (Hz).
Kita dapat melihat bahwa bentuk gelombang sinusoidal adalah tegangan bolak-balik (atau arus), yang bervariasi sebagai fungsi sinus sudut, 2πƒ. Frekuensi bentuk gelombang, ƒ ditentukan oleh jumlah siklus per detik. Harmonik adalah tegangan atau arus yang beroperasi pada frekuensi yang merupakan bilangan integer (bilangan bulat) dari frekuensi dasar.
Misalnya jika diberi bentuk gelombang dasar 50Hz, ini berarti frekuensi harmonik ke-2 adalah 100Hz (2 x 50Hz), harmonik ke-3 akan 150Hz (3 x 50Hz), ke-5 di 250Hz, ke-7 di 350Hz dan seterusnya.
Demikian juga, diberikan gelombang dasar 60Hz, frekuensi harmonik ke-2, ke-3, ke-5 dan ke-5 akan berada pada frekuensi masing-masing 120Hz, 180Hz, 240Hz dan 300Hz.
Jadi dengan kata lain, kita dapat mengatakan bahwa "harmonik" adalah kelipatan dari frekuensi dasar dan karena itu dapat dinyatakan sebagai: 2ƒ, 3ƒ, 4ƒ, dll seperti yang ditunjukkan.

Perhatikan bahwa bentuk gelombang merah di atas, adalah bentuk sebenarnya dari bentuk gelombang seperti yang terlihat oleh beban karena konten harmonik yang ditambahkan ke frekuensi dasar.
Gelombang mendasar juga bisa disebut gelombang harmonik-1. Oleh karena itu, harmonik kedua memiliki frekuensi dua kali lipat dari dasar, harmonik ketiga memiliki frekuensi tiga kali dasar dan harmonik keempat memiliki empat kali dasar seperti yang ditunjukkan pada kolom sebelah kiri.
Kolom sisi kanan menunjukkan bentuk gelombang kompleks yang dihasilkan sebagai akibat dari efek antara penambahan bentuk gelombang dasar dan bentuk gelombang harmonik pada frekuensi harmonik yang berbeda.
Perhatikan bahwa bentuk gelombang kompleks yang dihasilkan tidak hanya bergantung pada jumlah dan amplitudo frekuensi harmonik yang ada, tetapi juga pada hubungan fase antara frekuensi dasar atau frekuensi harmonik individu.
Kita dapat melihat bahwa gelombang kompleks terdiri dari bentuk gelombang dasar plus harmonik, masing-masing dengan nilai puncak dan sudut fase. Misalnya, jika frekuensi dasar diberikan sebagai; E = Vmax (2πƒt) , nilai harmonik akan diberikan sebagai:
Untuk harmonik kedua:
E2 = V2max (2*2πƒt) = V2max (4πƒt), = V2max (2πt)
Untuk harmonik ketiga:
E3 = V3max (3*2πƒt) = V3max (6πƒt), = V3max (3ωπt)
Untuk harmonik keempat:
E4 = V4max (4*2πƒt) = V4max (8πƒt), = V4max (4πt)
dan seterusnya.
Maka persamaan yang diberikan untuk nilai bentuk gelombang kompleks adalah:
persamaan harmonik frekuensi harmonik
ET = E1 + E2 + E3 + .... E(n) .dst.
ET = V1max sin(2πƒt) + V2max sin(4πƒt) + V3max sin(6πƒt) ... dst.
Harmonik umumnya diklasifikasikan berdasarkan nama dan frekuensi mereka, misalnya, harmonik ke-2 dari frekuensi dasar pada 100 Hz, dan juga dengan urutan mereka. Urutan harmonik mengacu pada rotasi fasor dari tegangan dan arus harmonik sehubungan dengan bentuk gelombang dasar dalam sistem 3-fasa 4-wire yang seimbang.
Harmonik urutan positif (4, 7, 10, ...) akan berputar dalam arah yang sama (maju) sebagai frekuensi dasar. Dimana harmonik urutan negatif (2, 5, 8, ...) berputar dalam arah yang berlawanan (terbalik) dari frekuensi dasar. Secara umum, harmonik urutan positif tidak diinginkan karena mereka bertanggung jawab atas panas berlebih dari konduktor, saluran listrik dan trafo/transformator karena penambahan bentuk gelombang.
Di sisi lain, harmonik urutan negatif bersirkulasi di antara fase-fase yang menciptakan masalah tambahan dengan motor karena rotasi fasor yang berlawanan melemahkan medan magnet berputar yang dibutuhkan oleh motor, dan terutama motor induksi, menyebabkan mereka menghasilkan torsi mekanis yang lebih sedikit.
Satu set harmonik khusus yang disebut "triplens" (kelipatan tiga) memiliki urutan rotasi nol. Triplens adalah kelipatan dari harmonik ketiga (ke-3, ke-6, ke-9, ...), dll, oleh karena itu namanya, dan karenanya dipindahkan dengan nol derajat. Nol harmonik urutan bersirkulasi antara fase dan netral atau ground.
Tidak seperti urutan harmonik urutan positif dan negatif yang membatalkan satu sama lain, urutan ketiga atau triplen harmonik tidak membatalkan. Alih-alih menambahkan secara hitung dalam kawat netral umum yang mengalami arus dari ketiga fase.
Hasilnya adalah bahwa amplitudo arus dalam kawat netral karena triplen harmonik ini bisa sampai 3 kali amplitudo arus fasa pada frekuensi dasar yang menyebabkannya menjadi kurang efisien dan terlalu panas. Kemudian kita dapat meringkas efek urutan sebagai kelipatan dari frekuensi dasar 50Hz sebagai:
Perhatikan bahwa urutan harmonik yang sama juga berlaku untuk bentuk gelombang dasar 60Hz.
Gelombang Harmonik hanya ada dalam jumlah yang cukup selama beberapa dekade terakhir sejak pengenalan drive elektronik untuk motor, kipas dan pompa, rangkaian switching catu daya seperti penyearah, konverter daya dan pengontrol daya thyristor serta sebagian besar fase elektronik non-linear terkontrol beban dan lampu neon frekuensi tinggi (hemat energi).
Hal ini terutama disebabkan oleh fakta bahwa arus terkontrol yang ditarik oleh beban tidak dengan setia mengikuti bentuk gelombang supply sinusoidal seperti dalam kasus penyearah atau rangkaian semikonduktor daya.
Harmonik dalam sistem distribusi tenaga listrik bergabung dengan frekuensi dasar (50Hz atau 60Hz) untuk menciptakan distorsi tegangan dan/atau bentuk gelombang arus. Distorsi ini menciptakan bentuk gelombang kompleks yang terdiri dari sejumlah frekuensi harmonik yang dapat memiliki efek buruk pada peralatan listrik dan saluran listrik.
Jumlah distorsi bentuk gelombang yang memberikan bentuk gelombang kompleks bentuknya yang khas berhubungan langsung dengan frekuensi dan besaran komponen harmonik yang paling dominan yang frekuensi harmoniknya adalah kelipatan (bilangan bulat) dari frekuensi dasar. Komponen harmonik yang paling dominan adalah harmonik orde rendah dari 2 ke 19 dengan triplens yang terburuk.
Ini karena Resistor adalah perangkat linier dan jika tegangan yang diterapkan adalah gelombang sinus, arus yang mengalir melalui itu juga merupakan gelombang sinus sehingga perbedaan fasa antara kedua gelombang sinusoidal adalah nol.
Secara umum ketika berhadapan dengan tegangan dan arus bolak-balik dalam rangkaian listrik, diasumsikan bahwa mereka murni dan berbentuk gelombang sinusoidal dengan hanya satu nilai frekuensi, yang disebut "frekuensi fundamental" yang ada, tetapi ini tidak selalu terjadi.
Dalam perangkat atau rangkaian listrik atau elektronik yang memiliki karakteristik tegangan-arus yang tidak linier, yaitu arus yang mengalir melalui itu tidak sebanding dengan tegangan yang diberikan.
Bentuk gelombang bolak-balik yang terkait dengan perangkat akan berbeda hingga lebih besar atau lebih kecil daripada bentuk gelombang sinusoidal yang ideal. Jenis-jenis gelombang ini biasanya disebut sebagai bentuk gelombang non-sinusoidal atau kompleks.
Bentuk gelombang kompleks dihasilkan oleh perangkat listrik umum seperti Induktor berinti besi, Transformator switching, balast elektronik dalam lampu pijar dan beban induktif lainnya serta tegangan output dan bentuk gelombang arus dari alternator AC, generator dan mesin listrik lainnya. Hasilnya adalah bahwa bentuk arus mungkin tidak gelombang sinusoidal meskipun bentuk gelombang tegangan.
Juga sebagian besar rangkaian switching catu daya elektronik seperti Penyearah, Thyristor, Transistor daya, konverter daya dan SSR (solid state relay) lainnya yang memutus dan memotong catu daya gelombang sinusoidal untuk mengendalikan daya motor, atau mengubah catu daya sinusoidal AC ke DC.
Rangkaian pengalihan tesis ini cenderung menarik arus hanya pada nilai puncak dari supply AC dan karena bentuk gelombang pengalihan non-sinusoidal, maka arus beban yang dihasilkan dikatakan mengandung Harmonik.
Bentuk gelombang kompleks non-sinusoidal dibangun dengan "menambahkan" bersama-sama serangkaian frekuensi gelombang sinus yang dikenal sebagai "Harmonik". Harmonik adalah istilah umum yang digunakan untuk menggambarkan distorsi bentuk gelombang sinusoidal oleh bentuk gelombang frekuensi yang berbeda.
Lalu apa pun bentuknya, bentuk gelombang yang kompleks dapat dipecah secara matematis menjadi komponen-komponen individualnya yang disebut frekuensi dasar dan sejumlah "frekuensi harmonik". Tetapi apa yang kita maksud dengan “frekuensi dasar”.
Frekuensi Dasar Gelombang Harmonik
Sebuah gelombang Dasar (atau harmonik pertama) adalah gelombang sinusoidal yang memiliki frekuensi pasokan. Dasarnya adalah frekuensi terendah atau dasar, ƒ di mana bentuk gelombang kompleks dibangun dan dengan demikian waktu periodik, Τ dari bentuk gelombang kompleks yang dihasilkan akan sama dengan waktu periodik frekuensi dasar.Mari kita perhatikan bentuk frekuensi dasar atau gelombang AC 1 harmonik seperti yang ditunjukkan.

Di mana: Vmax adalah nilai puncak dalam volt dan ƒ adalah frekuensi bentuk gelombang dalam Hertz (Hz).
Kita dapat melihat bahwa bentuk gelombang sinusoidal adalah tegangan bolak-balik (atau arus), yang bervariasi sebagai fungsi sinus sudut, 2πƒ. Frekuensi bentuk gelombang, ƒ ditentukan oleh jumlah siklus per detik. Harmonik adalah tegangan atau arus yang beroperasi pada frekuensi yang merupakan bilangan integer (bilangan bulat) dari frekuensi dasar.
Misalnya jika diberi bentuk gelombang dasar 50Hz, ini berarti frekuensi harmonik ke-2 adalah 100Hz (2 x 50Hz), harmonik ke-3 akan 150Hz (3 x 50Hz), ke-5 di 250Hz, ke-7 di 350Hz dan seterusnya.
Demikian juga, diberikan gelombang dasar 60Hz, frekuensi harmonik ke-2, ke-3, ke-5 dan ke-5 akan berada pada frekuensi masing-masing 120Hz, 180Hz, 240Hz dan 300Hz.
Jadi dengan kata lain, kita dapat mengatakan bahwa "harmonik" adalah kelipatan dari frekuensi dasar dan karena itu dapat dinyatakan sebagai: 2ƒ, 3ƒ, 4ƒ, dll seperti yang ditunjukkan.
Bentuk Gelombang Kompleks Karena gelombang Harmonik

Perhatikan bahwa bentuk gelombang merah di atas, adalah bentuk sebenarnya dari bentuk gelombang seperti yang terlihat oleh beban karena konten harmonik yang ditambahkan ke frekuensi dasar.
Gelombang mendasar juga bisa disebut gelombang harmonik-1. Oleh karena itu, harmonik kedua memiliki frekuensi dua kali lipat dari dasar, harmonik ketiga memiliki frekuensi tiga kali dasar dan harmonik keempat memiliki empat kali dasar seperti yang ditunjukkan pada kolom sebelah kiri.
Kolom sisi kanan menunjukkan bentuk gelombang kompleks yang dihasilkan sebagai akibat dari efek antara penambahan bentuk gelombang dasar dan bentuk gelombang harmonik pada frekuensi harmonik yang berbeda.
Perhatikan bahwa bentuk gelombang kompleks yang dihasilkan tidak hanya bergantung pada jumlah dan amplitudo frekuensi harmonik yang ada, tetapi juga pada hubungan fase antara frekuensi dasar atau frekuensi harmonik individu.
Kita dapat melihat bahwa gelombang kompleks terdiri dari bentuk gelombang dasar plus harmonik, masing-masing dengan nilai puncak dan sudut fase. Misalnya, jika frekuensi dasar diberikan sebagai; E = Vmax (2πƒt) , nilai harmonik akan diberikan sebagai:
Untuk harmonik kedua:
E2 = V2max (2*2πƒt) = V2max (4πƒt), = V2max (2πt)
Untuk harmonik ketiga:
E3 = V3max (3*2πƒt) = V3max (6πƒt), = V3max (3ωπt)
Untuk harmonik keempat:
E4 = V4max (4*2πƒt) = V4max (8πƒt), = V4max (4πt)
dan seterusnya.
Maka persamaan yang diberikan untuk nilai bentuk gelombang kompleks adalah:
persamaan harmonik frekuensi harmonik
ET = E1 + E2 + E3 + .... E(n) .dst.
ET = V1max sin(2πƒt) + V2max sin(4πƒt) + V3max sin(6πƒt) ... dst.
Harmonik umumnya diklasifikasikan berdasarkan nama dan frekuensi mereka, misalnya, harmonik ke-2 dari frekuensi dasar pada 100 Hz, dan juga dengan urutan mereka. Urutan harmonik mengacu pada rotasi fasor dari tegangan dan arus harmonik sehubungan dengan bentuk gelombang dasar dalam sistem 3-fasa 4-wire yang seimbang.
Harmonik urutan positif (4, 7, 10, ...) akan berputar dalam arah yang sama (maju) sebagai frekuensi dasar. Dimana harmonik urutan negatif (2, 5, 8, ...) berputar dalam arah yang berlawanan (terbalik) dari frekuensi dasar. Secara umum, harmonik urutan positif tidak diinginkan karena mereka bertanggung jawab atas panas berlebih dari konduktor, saluran listrik dan trafo/transformator karena penambahan bentuk gelombang.
Di sisi lain, harmonik urutan negatif bersirkulasi di antara fase-fase yang menciptakan masalah tambahan dengan motor karena rotasi fasor yang berlawanan melemahkan medan magnet berputar yang dibutuhkan oleh motor, dan terutama motor induksi, menyebabkan mereka menghasilkan torsi mekanis yang lebih sedikit.
Satu set harmonik khusus yang disebut "triplens" (kelipatan tiga) memiliki urutan rotasi nol. Triplens adalah kelipatan dari harmonik ketiga (ke-3, ke-6, ke-9, ...), dll, oleh karena itu namanya, dan karenanya dipindahkan dengan nol derajat. Nol harmonik urutan bersirkulasi antara fase dan netral atau ground.
Tidak seperti urutan harmonik urutan positif dan negatif yang membatalkan satu sama lain, urutan ketiga atau triplen harmonik tidak membatalkan. Alih-alih menambahkan secara hitung dalam kawat netral umum yang mengalami arus dari ketiga fase.
Hasilnya adalah bahwa amplitudo arus dalam kawat netral karena triplen harmonik ini bisa sampai 3 kali amplitudo arus fasa pada frekuensi dasar yang menyebabkannya menjadi kurang efisien dan terlalu panas. Kemudian kita dapat meringkas efek urutan sebagai kelipatan dari frekuensi dasar 50Hz sebagai:
Urutan Gelombang Harmonik
Nama
|
dasar
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Frekuensi, Hz
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
450
|
Urutan
|
+
|
-
|
0
|
+
|
-
|
0
|
+
|
-
|
0
|
Urutan
|
Rotasi
|
Efek Harmonisa
|
+
|
Meneruskan
|
Efek Pemanasan yang berlebihan
|
-
|
Membalikan
|
Masalah Torsi Motor
|
0
|
Tidak ada
|
Menambahkan Tegangan dan/atau Arus di Kawat Netral yang menyebabkan Pemanasan
|
Ringkasan Gelombang Harmonik
Gelombang Harmonik adalah bentuk gelombang frekuensi yang lebih tinggi ditumpangkan ke frekuensi dasar, yaitu frekuensi rangkaian, dan yang cukup untuk mengubah bentuk gelombangnya. Jumlah distorsi yang diterapkan pada gelombang dasar akan bergantung sepenuhnya pada jenis, jumlah dan bentuk harmonik yang ada.Gelombang Harmonik hanya ada dalam jumlah yang cukup selama beberapa dekade terakhir sejak pengenalan drive elektronik untuk motor, kipas dan pompa, rangkaian switching catu daya seperti penyearah, konverter daya dan pengontrol daya thyristor serta sebagian besar fase elektronik non-linear terkontrol beban dan lampu neon frekuensi tinggi (hemat energi).
Hal ini terutama disebabkan oleh fakta bahwa arus terkontrol yang ditarik oleh beban tidak dengan setia mengikuti bentuk gelombang supply sinusoidal seperti dalam kasus penyearah atau rangkaian semikonduktor daya.
Harmonik dalam sistem distribusi tenaga listrik bergabung dengan frekuensi dasar (50Hz atau 60Hz) untuk menciptakan distorsi tegangan dan/atau bentuk gelombang arus. Distorsi ini menciptakan bentuk gelombang kompleks yang terdiri dari sejumlah frekuensi harmonik yang dapat memiliki efek buruk pada peralatan listrik dan saluran listrik.
Jumlah distorsi bentuk gelombang yang memberikan bentuk gelombang kompleks bentuknya yang khas berhubungan langsung dengan frekuensi dan besaran komponen harmonik yang paling dominan yang frekuensi harmoniknya adalah kelipatan (bilangan bulat) dari frekuensi dasar. Komponen harmonik yang paling dominan adalah harmonik orde rendah dari 2 ke 19 dengan triplens yang terburuk.