Jembatan Maxwell: Rangkaian, Diagram Fasor & Aplikasi
Rangkaian yang digunakan untuk menghitung resistansi, induktansi, kapasitansi, frekuensi, dan induktansi timbal balik yang tidak diketahui disebut jembatan AC. Rangkaian ini beroperasi dengan sinyal tegangan AC. Jembatan ini bekerja berdasarkan prinsip rasio keseimbangan impedansi yang diperoleh oleh detektor nol dan menghasilkan hasil yang akurat.
Di beberapa rangkaian, penguat AC dapat digunakan sebagai pengganti detektor nol. Persamaan keseimbangan yang diperoleh dari rangkaian dapat digunakan untuk menentukan resistansi, kapasitansi, dan induktansi yang tidak diketahui dan juga frekuensi independen.
Jembatan AC digunakan dalam sistem komunikasi, rangkaian listrik dan elektronik yang kompleks dan masih banyak lagi. Ada berbagai jenis jembatan AC yang digunakan di rangkaian elektronik. Mereka adalah jembatan Maxwell, jembatan Maxwell Wein, jembatan Anderson, jembatan Hay, jembatan Owen, jembatan De Sauty, jembatan Schering, dan jembatan seri Wein.
Definisi Jembatan Maxwell
Jembatan Maxwell juga dikenal sebagai jembatan Wein Maxwell atau bentuk modifikasi jembatan Wheatstone atau jembatan kapasitansi induktansi Maxwell, terdiri dari empat lengan yang digunakan untuk mengukur induktansi yang tidak diketahui dalam hal kapasitansi dan resistansi yang dikalibrasi.
Ini dapat digunakan untuk mengukur nilai induktansi yang tidak diketahui dan membandingkannya dengan nilai standar. Ia bekerja berdasarkan prinsip perbandingan nilai induktansi yang diketahui dan tidak diketahui.
Ini menggunakan metode defleksi nol untuk menghitung induktansi dengan resistor dan kapasitor yang dikalibrasi paralel. Rangkaian jembatan Maxwell dikatakan beresonansi jika sudut fasa positif dari impedansi induktif dikompensasikan dengan sudut fasa negatif dari impedansi kapasitif (dihubungkan di lengan yang berlawanan). Oleh karena itu tidak akan ada arus yang mengalir melalui rangkaian dan tidak ada potensi di detektor null.
Rumus Jembatan Maxwell
Jika jembatan maxwell dalam kondisi seimbang, induktansi yang tidak diketahui dapat diukur dengan menggunakan kapasitor standar variabel. Rumus jembatan maxwell diberikan sebagai (dalam hal induktansi, resistansi, dan kapasitansi)
R1 = R2r3/R4
L1 = R2R3C4
Faktor kualitas rangkaian jembatan Maxwell diberikan sebagai,
Q = ωL1/R1 = ωC4R4
Rangkaian Jembatan Maxwell
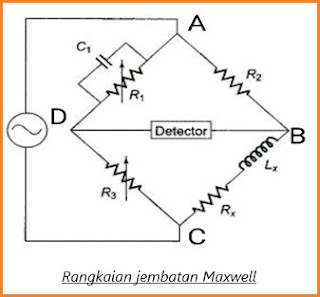
Rangkaian jembatan Maxwell terdiri dari 4 lengan yang dihubungkan dalam bentuk persegi atau belah ketupat. Dalam rangkaian ini, dua lengan berisi resistor tunggal, lengan lainnya berisi resistor dan induktor dalam kombinasi seri, dan lengan terakhir berisi resistor dan kapasitor dalam kombinasi paralel. Rangkaian jembatan Maxwell dasar ditunjukkan di bawah ini.
Sumber tegangan AC dan detektor nol dihubungkan secara diagonal ke rangkaian jembatan untuk mengukur nilai induktansi yang tidak diketahui dan dibandingkan dengan nilai yang diketahui.
Persamaan Jembatan Maxwell
Dari rangkaian tersebut, AB, BC, CD, dan DA adalah 4 lengan yang terhubung dalam bentuk belah ketupat.
AB dan CD adalah resistor R2 dan R3,
BC adalah kombinasi seri resistor dan induktor yang diberikan sebagai Rx dan Lx.
DA adalah kombinasi paralel resistor dan kapasitor yang diberikan sebagai R1 dan C1
Pertimbangkan Z1, Z2, Z3, dan ZX adalah impedansi dari 4 lengan rangkaian jembatan. Nilai untuk impedans ini diberikan sebagai,
Z1 = (R1+jwL1) [karena Z1 = R1+1/jwC1]
Z2 = R2
Z3 = R3
ZX = (R4+jwLX)
Atau
Z1 = R1 secara paralel dengan C1 yaitu, Y1 = 1/Z1
Y1 = 1/R1 + j ωC1
Z2 = R2
Z3 = R3
Zx = Rx secara seri dengan Lx = Rx + jωLx
Ambil persamaan keseimbangan rangkaian jembatan AC dasar sebagai berikut,
Z1Zx = Z2Z3
Zx = Z2Z3/Z1
Gantikan nilai impedansi rangkaian jembatan Maxwell dalam persamaan keseimbangan di atas. Kemudian,
Rx+jωLx = R2R3 ((1/R1)+jωC1)
Rx+jωLx = R2R3/R1+jωC1R2R3
Sekarang samakan suku nyata dan suku imajiner dari dua persamaan di atas,
Rx = R2R3/R1 dan Lx = C1R2R3
Q = ωLx/Rx = ωC1R2R3x R1/R2R3 = ωC1R
Dimana Q = faktor kualitas rangkaian jembatan
Rx = resistansi tidak diketahui
Lx = induktansi tidak diketahui
R2 dan R3 = resistansi non-induktif yang diketahui
C1 = kapasitor dihubungkan secara paralel ke resistor variabel R1
Diagram Fasor
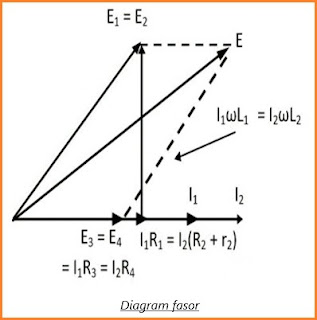
Jembatan Maxwell digunakan untuk mengukur induktansi yang tidak diketahui dari rangkaian dengan menggunakan resistor dan kapasitor yang dikalibrasi. Rangkaian jembatan ini membandingkan nilai induktansi yang diketahui dengan nilai standar. Rangkaian diagram fasor jembatan Maxwell dalam kondisi keseimbangan ditunjukkan di bawah ini.
Rangkaian jembatan Maxwell dikatakan dalam kondisi seimbang jika pergeseran fasa induktor dan kapasitor berlawanan satu sama lain. Itu berarti impedansi kapasitif dan impedansi induktif ditempatkan berlawanan satu sama lain di rangkaian jembatan. Arus I3 dan I4 dalam fasa dengan I1 dan I2. Dengan memvariasikan impedansi rangkaian jembatan, arus mungkin tertinggal di belakang sinyal tegangan AC yang diterapkan.
Kesalahan pengukuran dapat dihilangkan karena induktansi timbal balik antara kedua indikator. Karena kesalahan besar dapat terjadi karena kopling antara kumparan di rangkaian. Untuk mencapai kondisi keseimbangan rangkaian, variabel kapasitor dan resistor dihubungkan secara paralel. Induktansi yang diukur dalam kondisi keseimbangan tidak bergantung pada frekuensi.
Jenis Jembatan Maxwell
Berbagai jenis jembatan adalah
Jembatan Induktansi Maxwell
Jenis rangkaian jembatan ini digunakan untuk mengukur nilai induktansi yang tidak diketahui dari rangkaian dengan membandingkannya dengan nilai standar induktansi diri.
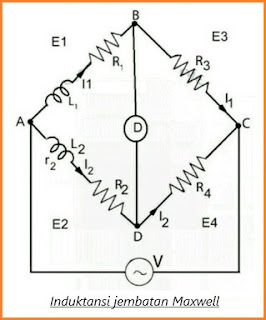
Dua lengan dari rangkaian jembatan dikenal resistansi non-induktif, satu lengan lainnya berisi induktansi variabel dengan resistor tetap secara seri, dan satu lengan lainnya berisi induktansi yang tidak diketahui secara seri dengan resistor.
Sumber tegangan AC dan detektor nol terhubung melintasi persimpangan rangkaian. Diagram rangkaian ditunjukkan di bawah ini.
Pada kondisi keseimbangan, rumus rangkaian induktansi Maxwell diberikan sebagai,
Dimana L1 = Induktansi tidak diketahui dengan resistor R1
R2 dan R3 adalah resistansi non-induktif
L2 adalah induktansi variabel dengan Resistensi r2 tetap
R2 adalah resistor variabel yang di seri dengan L2
Induktansi Kapasitansi Jembatan Maxwell
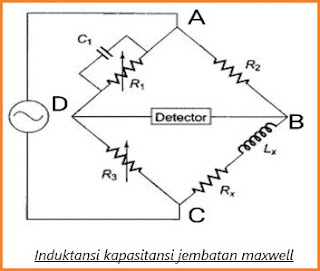
Jenis rangkaian jembatan ini digunakan untuk mengukur nilai induktansi yang tidak diketahui dengan membandingkannya dengan kapasitor standar variabel. Sinyal tegangan AC dan detektor nol terhubung di persimpangan.
Dari rangkaian, kita dapat mengamati bahwa,
Satu lengan berisi kapasitor standar variabel C1 secara paralel dengan variabel resistansi non-induktif R1
Dua lengan lainnya mengandung resistor non-induktif R2 dan R3 yang diketahui
Lengan lain berisi induktansi Lx yang tidak diketahui dengan resistor Rx secara seri yang nilainya akan diukur dan dibandingkan dengan nilai yang diketahui.
Ekspresi kapasitansi induktansi Maxwell diberikan sebagai, (dalam kondisi seimbang)
Q = faktor kualitas rangkaian jembatan Maxwell
Kelebihan dari Jembatan Maxwell
Keuntungannya adalah
- Pada kondisi keseimbangan, rangkaian jembatan tidak bergantung pada frekuensi
- Ini membantu mengukur berbagai nilai induktansi pada frekuensi audio dan daya
- Untuk mengukur nilai induktansi secara langsung, skala resistansi yang dikalibrasi digunakan.
- Ini digunakan untuk mengukur kisaran induktansi yang tinggi dan dibandingkan dengan nilai standar.
Kekurangan dari Jembatan Maxwell
Kelemahanya adalah
- Kapasitor tetap di rangkaian jembatan Maxwell dapat menciptakan interaksi antara resistansi dan keseimbangan reaktansi.
- Tidak sesuai untuk mengukur rentang faktor kualitas yang tinggi (nilai Q> = 10)
- Kapasitor standar variabel yang digunakan dalam rangkaian sangat mahal.
- Ini tidak digunakan untuk mengukur faktor kualitas rendah (nilai Q) karena kondisi keseimbangan rangkaian. Oleh karena itu digunakan untuk kumparan kualitas menengah.
Aplikasi Jembatan Maxwell
Penggunaannya adalah
- Digunakan dalam sistem komunikasi
- Digunakan di rangkaian elektronik
- Digunakan dalam rangkaian daya dan frekuensi audio
- Digunakan untuk mengukur nilai induktansi rangkaian yang tidak diketahui dan dibandingkan dengan nilai standar.
- Digunakan untuk mengukur kumparan kualitas sedang.
- Digunakan dalam rangkaian filter, instrumentasi, rangkaian linier dan non-linier
- Digunakan di rangkaian konversi daya.
Pertanyaan
1). Apa itu jembatan AC dan DC?
Jembatan AC dan jembatan DC digunakan untuk mengukur komponen yang tidak diketahui seperti induktansi, kapasitansi, dan resistansi. Atau ukur impedansi rangkaian yang tidak diketahui.
Berbagai jenis jembatan AC adalah jembatan Maxwell, jembatan Wien Maxwell, jembatan Anderson, jembatan Hay, jembatan Owen, jembatan De Sauty, jembatan Schering, dan jembatan seri Wein.
Jembatan DC digunakan untuk mengukur resistansi yang tidak diketahui di rangkaian jembatan. Berbagai jenis jembatan DC adalah jembatan Wheatstone, jembatan Kelvin, dan jembatan pengukur regangan.
2). Jembatan mana yang peka frekuensi?
Jembatan Wien peka frekuensi.
3). Apa tujuan rangkaian jembatan?
Tujuan dari rangkaian jembatan adalah untuk memperbaiki arus listrik dalam catu daya dan mengukur impedansi rangkaian yang tidak diketahui dan membandingkannya dengan nilai yang diketahui.
4). Apa rumus induktansi diri?
Ketika fluks diketahui, rumus induktansi diri diberikan sebagai,
L = NΦm/I.
Dimana 'L' adalah induktansi diri di Henry
'Φm' adalah fluks magnet pada kumparan
'N' adalah jumlah belokan
'I' adalah arus yang mengalir melalui kumparan di Ampere.
5). Apa itu Osilator RC dan LC?
Osilator LC menggunakan rangkaian tangki induktor-kapasitor dan merupakan jenis osilator umpan balik positif untuk menghasilkan osilasi berkelanjutan.
Osilator linier yang menggunakan resistor dan kapasitor untuk membentuk jaringan RC dengan umpan balik positif disebut osilator RC. Ia juga dikenal sebagai osilator sinusoidal.
Jadi ini semua gambaran umum tentang definisi rangkaian jembatan Maxwell , jenis, rumus, persamaan, jenis, aplikasi, kelebihan, dan kekurangan.